【机器学习】周志华西瓜书第十章降维与度量学习习题--实现k近邻分类器,在西瓜数据集3.0上比较分界边界与决策树分类边界的异同
(1)问题理解与分析
实现k近邻分类器,在西瓜数据集3.0上比较分界边界与决策树分类边界的异同。
(2)kNN算法原理阐述
k近邻(k-Nearest Neighbor,简称kNN)学习是一种常用的监督学习方法,其工作机制非常简单:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个“邻居”的信息来进行预测。通常,在分类任务中可使用“投票法”,即选择这k个样本中出现最多的类别标记作为预测结果;在回归任务中可使用“平均法”,即将这k个样本的实值输出标记的平均值作为预测结果;还可基于距离远近进行加权平均或加权投票,距离越近的样本权重越大。与前面介绍的学习方法相比,k近邻学习有一个明显的不同之处:它似乎没有显式的训练过程。事实上,它是“懒惰学习”(lazy learning)的著名代表,此类学习技术在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理;相应的,那些在训练阶段就对样本进行学习处理的方法,称为“急切学习”(eager learning)。
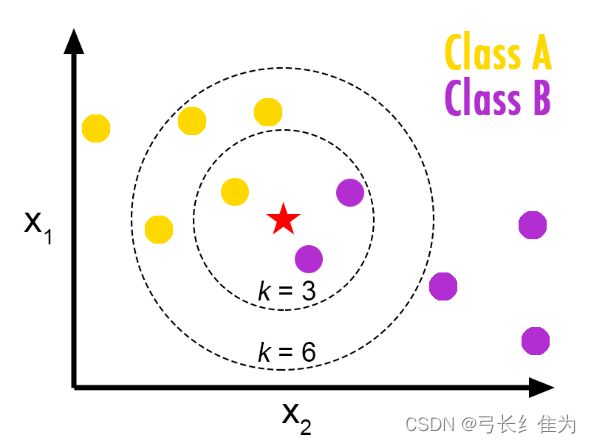
如上图所示,当kNN的k定义为3,则在五角星最近的3个点内,分类为B的点最多,则五角星的分类为B;当kNN的k定义为6,则在五角星最近的6个点内,分类为A的点最多,则五角星的分类为A。显然,当k取不同值时,分类结果会有显著不同。另一方面,若采用不同的距离计算方式,则找出的“近邻”可能有显著差别,从而也会导致分类结果有显著不同。
(3)kNN算法设计思路
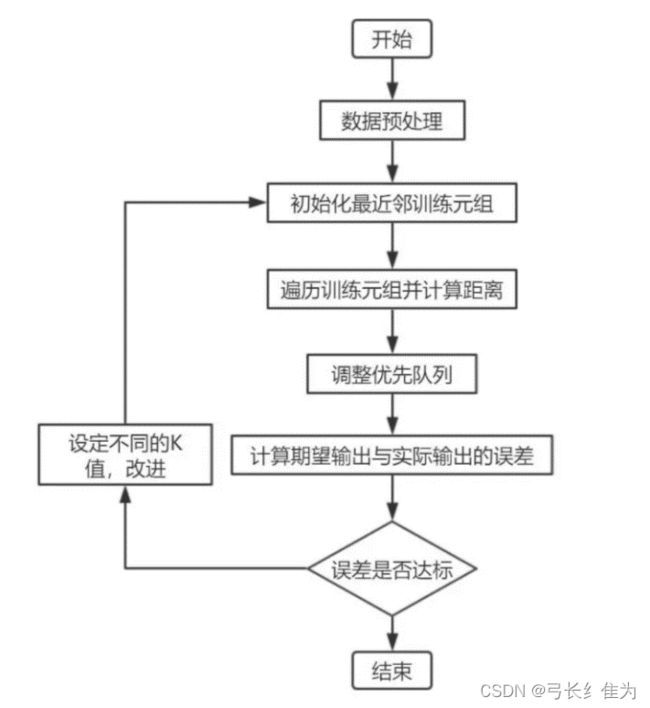
kNN算法实验流程图如下:
(4)实验数据的选择(训练集和测试集划分)、实验结果展示、优化与分析
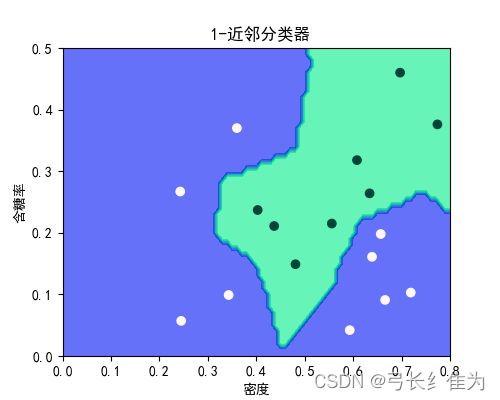
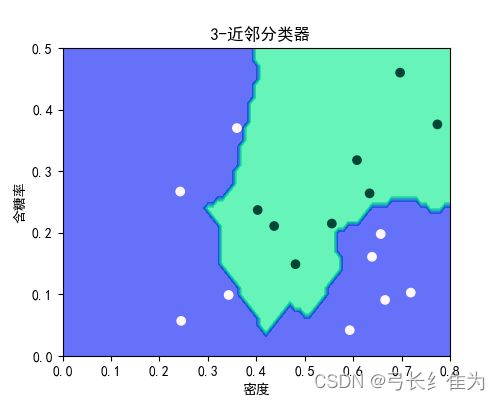
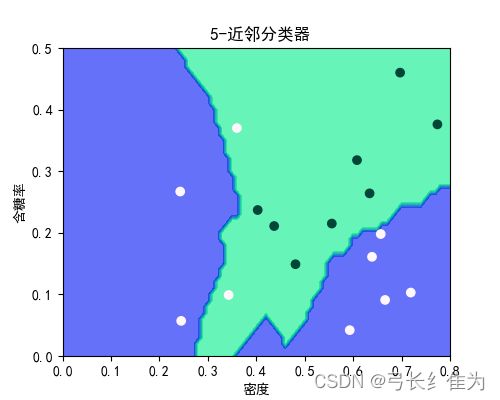
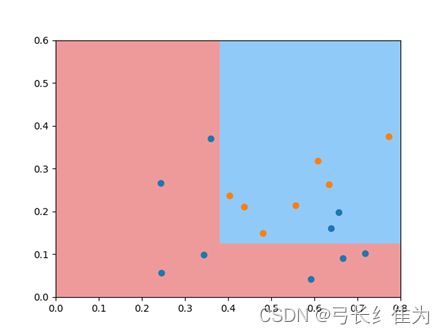
本实验使用的数据集是西瓜数据集3.0a,只使用连续型属性。当k=1时,17个样本预测正确17个,正确率为100%;当k=3时,17个样本预测正确17个,正确率为100%;当k=5时,17个样本预测正确15个,正确率为88.2%。作为对比,决策树17个样本预测正确15个,正确率为88.2%。当k值选择合理时,kNN算法的性能要优于决策树。
决策树:
kNN:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def knn(train, test, num):
# train,test,num分别为训练集,测试集,近邻个数
output = [] # 预测分类结果
m, n = len(train), len(test)
for i in range(n):
dist_ij = []
for j in range(m):
d = np.linalg.norm(test[i, :] - train[j, :-1]) # 求范数
dist_ij.append((j, d))
id_min = sorted(dist_ij, key=lambda x: x[1])[:num]
rate = [train[i[0], -1] for i in id_min]
if sum(rate) / num >= 0.5: # 当两类得票数相等时,优先划分为正例
output.append(1)
else:
output.append(0)
return output
data=pd.read_csv('D:\学习\专业主干课\机器学习\数据集\watermelon3_0a.csv',header=None)
data=data.values
print(data.shape)
#data = data[:,2:]
a = np.arange(0, 1.01, 0.01)
b = np.arange(0, 0.61, 0.01)
x, y = np.meshgrid(a, b)
k = 5
z = knn(data, np.c_[x.ravel(), y.ravel()], k)
z = np.array(z).reshape(x.shape)
fig, ax = plt.subplots(1, 1, figsize=(5, 4))
ax.contourf(x, y, z, cmap = plt.cm.winter, alpha=.6)
label_map = {1: 'good', 0: 'bad'}
ax.scatter(data[:, 0], data[:, 1], c=data[:, 2], cmap=plt.cm.PuBuGn)
ax.set_xlim(0, 0.8)
ax.set_ylim(0, 0.5)
ax.set_ylabel('含糖率')
ax.set_xlabel('密度')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
ax.set_title(' %s-近邻分类器' % k)
plt.show()决策树:
# -*- coding: utf-8 -*-
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import matplotlib.pylab as plt
import numpy as np
data=pd.read_csv('D:\学习\专业主干课\机器学习\数据集\watermelon3_0a.csv')
data=data.values
X=data[:,0:2]
y=data[:,2]
# 查看数据分布
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == 2, 0], X[y == 2, 1])
plt.show()
# 建设一颗决策树
tree_clf = DecisionTreeClassifier(criterion='entropy', max_depth=2)
tree_clf.fit(X, y)
# 导出决策树图形
export_graphviz(tree_clf,
out_file="iris_tree.dot",
rounded=True,
filled=True
)
# 决策边界绘制函数
def plot_decision_boundary(model, x):
# 生成网格点坐标矩阵,得到两个矩阵
M, N = 500, 500
x0, x1 = np.meshgrid(np.linspace(0, 0.8, M), np.linspace(0, 0.6, N))
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
z = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.pcolormesh(x0, x1, z, cmap=custom_cmap)
# 绘制决策边界
plot_decision_boundary(tree_clf, X)
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == 2, 0], X[y == 2, 1])
plt.show()
# 查看特征重要性
print(tree_clf.feature_importances_)