knn最近邻算法_k最近邻knn算法

knn最近邻算法

目录： (Table of Contents:)

1. What is KNN?
   什么是KNN？
2. Working of KNN algorithm
   KNN算法的工作
3. What happens when K changes?
   当K变化时会发生什么？
4. How to select appropriate K?
   如何选择合适的K？
5. Limitation of KNN
   KNN的局限性
6. Real-world application of KNN
   KNN的实际应用
7. Conclusion
   结论

1.什么是KNN？ (1. What is KNN?)

K nearest neighbors (KNN) is a supervised machine learning algorithm. A supervised machine learning algorithm’s goal is to learn a function such that f(X) = Y where X is the input, and Y is the output. KNN can be used both for classification as well as regression. In this article, we will only talk about classification. Although for regression, there is just a minute change.

K最近邻居(KNN)是一种受监督的机器学习算法。 监督式机器学习算法的目标是学习一个函数，使得f(X)= Y，其中X是输入，Y是输出。 KNN可用于分类和回归。 在本文中，我们仅讨论分类。 尽管要进行回归，但只有一分钟的变化。

The properties of KNN is that it is a lazy learning algorithm and a non-parametric method.

KNN的特性是它是一种惰性学习算法和非参数方法。

Lazy learning means the algorithm takes almost zero time to learn because it only stores the data of the training part (no learning of a function). The stored data will then be used for the evaluation of a new query point.

惰性学习意味着该算法几乎只需花费零时间进行学习，因为它仅存储训练部分的数据(不学习功能)。 然后，存储的数据将用于评估新的查询点。

The non-parametric method refers to a method that does not assume any distribution. Therefore, KNN does not have to find any parameter for the distribution. While in the parametric method, the model finds new parameters, which in turn will be used for the prediction purpose. The only hyperparameter (provided by the user to the model) KNN has is K, which is the number of points that needs to be considered for comparison purpose.

非参数方法是指不假定任何分布的方法。 因此，KNN不必为分布找到任何参数。 在参数化方法中，模型会找到新参数，这些参数又将用于预测目的。 KNN唯一的超参数(由用户提供给模型)是K，这是比较目的需要考虑的点数。

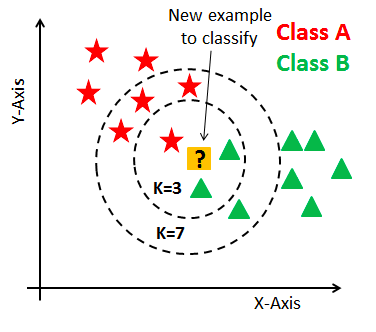
Source 资源

In the above image, yellow is the query point, and we want to know which class it belongs to (red or green).

在上图中，黄色是查询点，我们想知道它属于哪个类(红色或绿色)。

With K=3, the 3 nearest neighbors of the yellow point are considered, and the class is assigned to the query point based on the majority (e.g., 2 green and 1 red — then it is of green class). Similarly, for K=5, 5 nearest neighbors are considered for the comparison, and the majority will decide which class the query point belongs to. One thing to notice here, if the value of K is even, it might create problems when taking a majority vote because the data has an even number of classes (i.e., 2). Therefore, choose K as an odd number when the data has an even number of classes and even number when the data has an odd number of classes.

在K = 3的情况下，考虑了黄点的3个最近邻居，并且基于多数(例如2个绿色和1个红色-那么它是绿色类别)将类别分配给查询点。 类似地，对于K = 5，将考虑5个最近的邻居进行比较，并且大多数将决定查询点属于哪个类。 这里要注意的一件事是，如果K的值为偶数，则在多数表决中可能会产生问题，因为数据具有偶数个类(即2)。 因此，当数据具有偶数个类别时，选择K作为奇数；当数据具有奇数个类别时，选择K作为奇数。

2. KNN算法的工作 (2. Working of KNN algorithm)

In the training phase, the model will store the data points. In the testing phase, the distance from the query point to the points from the training phase is calculated to classify each point in the test dataset. Various distances can be calculated, but the most popular one is the Euclidean distance (for smaller dimension data).

在训练阶段，模型将存储数据点。 在测试阶段，计算从查询点到训练阶段的点之间的距离，以对测试数据集中的每个点进行分类。 可以计算各种距离，但是最流行的是欧几里得距离(用于较小尺寸的数据)。

Euclidean distance between a query point (q) and a training data point (p) is defined as

查询点(q)和训练数据点(p)之间的欧式距离定义为

Source 资源

Other distance measures such as Manhattan, Hamming, and Chebyshev distance can also be used based on the data, which is out of the scope of this article.

也可以根据数据使用其他距离度量，例如Manhattan，Hamming和Chebyshev距离，这不在本文的讨论范围之内。

Let’s learn it with an example:

让我们用一个例子来学习它：

We have 500 N-dimensional points, with 300 being class 0 and 200 being class 1.

我们有500个N维点，其中300个是0类，而200个是1类。

The procedure for calculating the class of query point is:

计算查询点类别的过程是：

1. The distance of all the 500 points is calculated from the query point.
   从查询点算出所有500个点的距离。
2. Based on the value of K, K nearest neighbors are used for the comparison purpose.
   基于K的值，将K个最近的邻居用于比较目的。
3. Let’s say K=7, 4 out of 7 points are of class 0, and 3 are of class 1. Then based on the majority, the query point p is assigned as class 0.
   假设K = 7，则7个点中有4个是0类，而3个是1类。然后基于多数，将查询点p分配为0类。

3. K改变时会发生什么？ (3. What happens when K changes?)

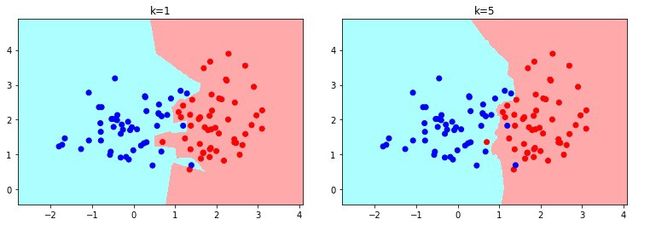
Decision Surface separating the red and blue class with k=1 (left) and k=5 (right). Image by author 决策面用k = 1(左)和k = 5(右)分隔红色和蓝色类。 图片作者

K=1 means that it will take one nearest neighbor and classify the query point based on that. The surface that divides the classes will be very uneven (many vertices).

K = 1表示它将采用一个最近的邻居，并根据该邻居对查询点进行分类。 划分类别的表面将非常不平坦(许多顶点)。

The problem that arises here is if an outlier is present in the data, the decision surface considers that as a data point. Due to this, KNN will perform exceptionally well on the training dataset but will misclassify many points on the test dataset (unseen data). This is considered as overfitting, and therefore, KNN is sensitive to outliers.

此处出现的问题是，如果数据中存在异常值，则决策面会将其视为数据点。 因此，KNN将在训练数据集上表现异常出色，但会错误分类测试数据集上的许多点(看不见的数据)。 这被认为是过度拟合，因此，KNN对异常值敏感。

As the value of K increases, the surface becomes smooth and will not consider the outliers as data points. This will better generalize the model on the test dataset also.

随着K值的增加，表面变得平滑，并且不会将离群值视为数据点。 这也将更好地将模型推广到测试数据集。

If K value is extremely large, the model will underfit and will be unable to classify the new data point. For example, if K is equal to the total number of data points, no matter where the query point lies, the model will always classify the query point based on the majority class of the whole dataset.

如果K值非常大，则模型将无法拟合，并且将无法对新数据点进行分类。 例如，如果K等于数据点的总数，则无论查询点位于何处，模型都将始终基于整个数据集的多数类对查询点进行分类。

Choosing a correct value K will give accurate results. But how to choose that?

选择正确的值K将得出准确的结果。 但是如何选择呢？

4.如何选择合适的K？ (4. How to select appropriate K?)

In real-world problems, the dataset is separated into three parts, namely, training, validation, and test data. In KNN, the training data points get stored, and no learning is performed. Validation data is to check the model performance, and the test data is used for prediction.

在实际问题中，数据集分为三个部分，即训练，验证和测试数据。 在KNN中，将存储训练数据点，并且不执行任何学习。 验证数据用于检查模型性能，测试数据用于预测。

To select optimal K, plot the error of model (error = 1 — accuracy) on training as well as on the validation dataset. The best K is where the validation error is lowest, and both training and validation errors are close to each other.

要选择最佳K，请在训练以及验证数据集上绘制模型误差(误差= 1-精度)。 最佳K是验证误差最低的地方，训练和验证误差彼此接近。

Source 来源

5. KNN的局限性 (5. Limitation of KNN)

Time complexity and space complexity is enormous, which is a major disadvantage of KNN. Time complexity refers to the time model takes to evaluate the class of the query point. Space complexity refers to the total memory used by the algorithm. If we have n data points in training and each point is of m dimension. Then time complexity is of order O(nm), which will be huge if we have higher dimension data. Therefore, KNN is not suitable for high dimensional data.

时间复杂度和空间复杂度是巨大的，这是KNN的主要缺点。 时间复杂度是指时间模型用来评估查询点的类。 空间复杂度是指算法使用的总内存。 如果我们在训练中有n个数据点，而每个点都是m维。 然后，时间复杂度约为O(nm)，如果我们具有更高维度的数据，它将非常庞大。 因此，KNN不适合用于高维数据。

Another disadvantage is if the data point is far away from the classes present (no similarity), KNN will classify the point even if it is an outlier. In order to overcome the problem of time complexity, algorithms such as KD-Tree and Locality Sensitive Hashing (LSH) can be used, which is not covered in this article.

另一个缺点是，如果数据点与现有的类相距太远(没有相似性)，则KNN将对点进行分类，即使它是一个异常值也是如此。 为了克服时间复杂性的问题，可以使用诸如KD-Tree和本地敏感哈希(LSH)之类的算法，本文不做介绍。

6. KNN的实际应用 (6. Real-world application of KNN)

1. KNN can be used for Recommendation Systems. Although in the real world, more sophisticated algorithms are used for the recommendation system. KNN is not suitable for high dimensional data, but KNN is an excellent baseline approach for the systems. Many companies make a personalized recommendation for its consumers, such as Netflix, Amazon, YouTube, and many more.
   KNN可用于推荐系统。 尽管在现实世界中，推荐系统仍使用更复杂的算法。 KNN不适合用于高维数据，但是KNN是系统的出色基线方法。 许多公司为其消费者提供个性化推荐，例如Netflix，亚马逊，YouTube等。
2. KNN can search for semantically similar documents. Each document is considered as a vector. If documents are close to each other, that means the documents contain identical topics.
   KNN可以搜索语义相似的文档。 每个文档都被视为向量。 如果文档彼此靠近，则意味着文档包含相同的主题。
3. KNN can be effectively used in detecting outliers. One such example is Credit Card fraud detection.
   KNN可以有效地用于检测异常值。 这样的例子之一就是信用卡欺诈检测。

7.结论 (7. Conclusion)

K- Nearest Neighbors (KNN) identifies the nearest neighbors given the value of K. It is lazy learning and non-parametric algorithm. KNN works on low dimension dataset while faces problems when dealing with high dimensional data.

K-最近邻居(KNN)在给定K值的情况下识别最近邻居。这是惰性学习和非参数算法。 KNN适用于低维数据集，但在处理高维数据时会遇到问题。

翻译自: https://towardsdatascience.com/k-nearest-neighbors-knn-algorithm-23832490e3f4

knn最近邻算法