在本文中,我们将回顾特性选择技术并回答为什么它很重要以及如何使用python实现它。
本文还可以帮助你解答以下的面试问题:
- 什么是特征选择?
- 说出特性选择的一些好处
- 你知道哪些特征选择技巧?
- 区分单变量、双变量和多变量分析。
- 我们能用PCA来进行特征选择吗?
- 前向特征选择和后向特征选择的区别是什么?
什么是特征选择,为什么它很重要?
特性选择是选择与ML模型更加一致、非冗余和更相关的基本特性的过程。在ML项目中使用特性选择是必要的,因为:
- 它有助于减少数据集的大小和复杂性,并且可以使用更少的时间来训练模型及进行推理;
- 具有较少特征的简单机器学习模型更容易理解和解释;
- 它可以避免过度拟合。更多特征使模型变得更加复杂,并带来维度灾难(误差随着特征数量的增加而增加)。
特征选择方法有哪些?
有两种常见的方法可以处理特征选择:
1、前向特征选择。使用一个特征(或一小部分)拟合模型并不断添加特征,直到新加的模型对ML 模型指标没有影响。可以使用相关分析等方法(例如,基于 Pearson 系数),或者您可以从单个特征或特征子集开始拟合模型。
2、向后特征选择。这是 与1的相反方法。使用这种方法,可以从完整的特征集开始,然后迭代地逐个减少功能,减少特征的同时只要 ML 模型指标保持不变即可。
我们可以将一些流行的方法总结成以下几种分类:
- Filtered-based基于过滤的方法:这种方法是最直接的,这种特征的选择独立于任何机器学习算法。使用统计数据(例如 Pearson 相关系数、LDA 等),根据每个特征如何影响目标结果来选择重要特征。这是计算密集度最低且速度最快的方法。
- Wrapper 基于包装器方法:这种方法根据 ML 训练指标结果选择特征。每个子集在训练后得到一个分数,然后添加或删除特征,并在最终在达到所需的 ML 指标阈值时停止,这种方法可以是前向、后向或递归的。这是计算最密集的方法,因为需要训练许多 ML 模型,并且逐一进行判断选择。
- Embedded 基于嵌入的方法:这种方法更加复杂,它将上面两种方法组合在一起。这种方法最流行的例子是 LASSO 和树型算法。
使用Python进行特征选择
本文将使用一个金融科技数据集,该数据集包含过去贷款申请人的数据,如信用等级、申请人收入、DTI和其他特征。最后的目标是使用ML预测贷款申请人是否可能违约(无法支付贷款)。这有助于企业做出决策,例如拒绝贷款申请、减少贷款金额或以更高的利率向风险较高的申请人放贷。我用来运行代码的环境是Kaggle。
让我们开始并加载数据集:
%matplotlib inline
from matplotlib import pyplot as plt
pd.set_option('display.float_format', lambda x: '%.0f' % x)
loan = pd.read_csv('../input/lending-club/accepted_2007_to_2018Q4.csv.gz', compression='gzip', low_memory=True)
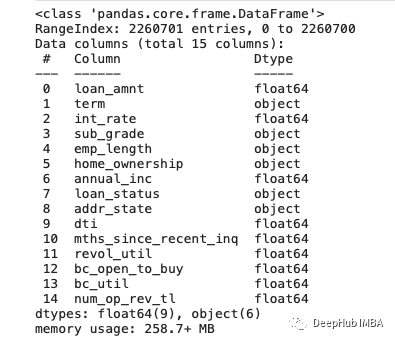
loan.info数据集包含超过200万行(我们称之为样本)和超过150个特征。这是相当大的数据量,这些数据通常包含了很多“噪声”它对我们的ML工作没有任何的帮助,因此我们需要在ML训练发生之前验证数据的质量和适用性。
第一步:获得专业的领域知识
对如此详尽的特征列表进行分析可能需要大量的计算资源和时间。所以我们需要详细了解每个数据集的属性。
咨询并询问行业的专家哪些特征是必要的;例如,在金融科技数据集的例子中可能需要咨询每天执行贷款评估的信贷员。信贷员将确切地知道是什么驱动了他们的决策过程(我们其实是希望将这部分过程通过ML实现自动化)。
假设我们已得到了以下建议(请参阅下面的代码片段)。虽然我们应该对这些建议保持谨慎,但它为我们开始初步工作提供了一个很好的基础,我们可以进一步改进。
loans = loan[['id', 'loan_amnt', 'term','int_rate', 'sub_grade', 'emp_length','grade', 'annual_inc', 'loan_status', 'dti', 'mths_since_recent_inq', 'revol_util', 'bc_open_to_buy', 'bc_util', 'num_op_rev_tl']]
#remove missing values
loans = loans.dropna()花合理的时间来理解数据集中每个特征的含义:
- loan_amnt -借款人申请贷款的清单金额。
- term -偿还贷款的次数,其中的值以月为单位,可以是36或60。
- int_rate -贷款的利率
- sub_grade -根据借款人的信用记录分配贷款等级分数
- emp_length -借款者的就业年限。
- home_ownership-借款人提供的房屋所有权状况(例如,租金、所有权、抵押贷款等)
- annual_inc -借款人提供的自我报告的年收入
- addr_state-借款人在贷款申请中提供的状态
- dti -用借款人每月偿还的债务总额(不包括按揭)除以借款人每月收入计算的比率。
- mths_since_recent_inq-最近一次查询的月份
- revol_util - 循环额度利用率,或借款人使用的信贷金额相对于所有可用的循环信贷。
- bc_open_to_buy - 银行卡的总开放购买量
- bc_util - 所有银行卡账户的总流动余额与高信用/信用限额的比率
- num_op_rev_tl - 开户数
- loan_status - 当前贷款状态(例如,完全支付或注销)。这就是我们要用模型预测的标签。
在进行下一步工作之前,需要先执行数据处理步骤。步骤包括缺失值、异常值和分类特征处理。
loans = loans.dropna()
q_low = loans["annual_inc"].quantile(0.08)
q_hi = loans["annual_inc"].quantile(0.92) loans = loans[(loans["annual_inc"] < q_hi) & (loans["annual_inc"] > q_low)]
loans = loans[(loans['dti'] <=45)]
q_hi = loans['bc_open_to_buy'].quantile(0.95)
loans = loans[(loans['bc_open_to_buy'] < q_hi)]
loans = loans[(loans['bc_util'] <=160)]
loans = loans[(loans['revol_util'] <=150)]
loans = loans[(loans['num_op_rev_tl'] <=35)]
cleaner_app_type = {"term": {" 36 months": 1.0, " 60 months": 2.0},
"sub_grade": {"A1": 1.0, "A2": 2.0, "A3": 3.0, "A4": 4.0,
"A5": 5.0, "B1": 11.0, "B2": 12.0, "B3": 13.0, "B4": 14.0,
"B5": 15.0, "C1": 21.0, "C2": 22.0, "C3": 23.0, "C4":
24.0, "C5": 25.0, "D1": 31.0, "D2": 32.0, "D3": 33.0,
"D4": 34.0, "D5": 35.0, "E1": 41.0, "E2": 42.0, "E3":
43.0, "E4": 44.0, "E5": 45.0, "F1": 51.0, "F2": 52.0,
"F3": 53.0, "F4": 54.0, "F5": 55.0, "G1": 61.0, "G2":
62.0, "G3": 63.0, "G4": 64.0, "G5": 65.0, },
"emp_length": {"< 1 year": 0.0, '1 year': 1.0, '2 years': 2.0,
'3 years': 3.0, '4 years': 4.0, '5 years': 5.0, '6 years':
6.0, '7 years': 7.0, '8 years': 8.0, '9 years': 9.0, '10+
years': 10.0 }
}
loans = loans.replace(cleaner_app_type)在预选特征之后,下一步是进行单变量分析。分析单个特征时可以使用的最常见的两种技术:1)删除低方差(超过90%)的特征;2)删除有大量缺失值的特征。
低方差:假设有两个特征,1)性别只包含一个性别值(例如,女性),2)年龄包含30到50岁之间的不同值。在这种情况下,性别特征的方差很小,因为这个属性中的值都是相同的,在模型训练时,它不会帮助模型找到任何模式;因此我们可以直接删除这个特征。
这种方式得实现非常简单,可以使用sklearn得VarianceThreshold函数。下面的代码将识别那些在至少90%的实例中相同的特性。
from sklearn.feature_selection import VarianceThreshold
variance = VarianceThreshold(threshold = (.9 * (1 - .9)))
variance.fit(loans)
variance.get_support()可以看到在我们的案例中没有低方差的特征,所以不需要删除。
缺失值:在这组特征中没有任何包含大量缺失值的特征;因此,我们将跳过这一步。以前我们也发过处理缺失值的文章,如果你对这部分感兴趣,可以搜索查看。
第二步:识别高度相关的特征
第二步是识别特征的多重共线性。我们使用双变量分析来找出两组变量之间是否有关系(相关)。
利用这些相关性,你可以得到以下的结论:
- 一个或多个变量依赖于另一个变量,可能导致多重共线性;
- 相关性可以帮助预测一个变量与另一个变量的关系,表明存在因果关系;
- 在业务层面上可以了解标签结果的因素,在我们的例子中了解每个特性如何影响贷款支付结果
当数据集的特征之间具有高度的正相关或负相关时,ML模型可能会受到多重共线性的影响。高度相关的特征可能提供相同的信息。在这种情况下可能会导致扭曲或误导的结果,为了解决这个问题,我们可以只保留一个特征,删除多余的特征,这样是不丢失任何信息的。
比如月薪和年薪;虽然它们可能不一样,但它们可能有相同的模式。像逻辑回归和线性回归这样的模型对这个问题很敏感,如果用这样的冗余特征训练模型,可能会产生误导的结果。因此我们应该以消除其中一个为目标。
注意:决策树和增强树等算法不受多重共线性的影响。
如何处理多重共线性?
有很多方法可以处理它。检测高度相关特征的最简单方法是使用 Pearson 相关系数并删除十分(~90%)相关特征。主成分分析(PCA)也可以用作降维算法。它通常用于降维,它将每个数据点仅投影到前几个主成分上获得低维数据的同时尽可能多地保留数据的变化。
这里我们使用pandas_profiling来进行分析
from pandas_profiling import ProfileReport
profile = ProfileReport (loans, title = 'Loans Defaults Prediction', html = {'style': {'full_width': True }})
profile你会发现Pearson和Phik之间不同类型的相关性。当数据中包含未处理的分类特性时,Phik是非常好用的。例如,下面的“grade”分类特征,它在相关矩阵上绘制得很好:
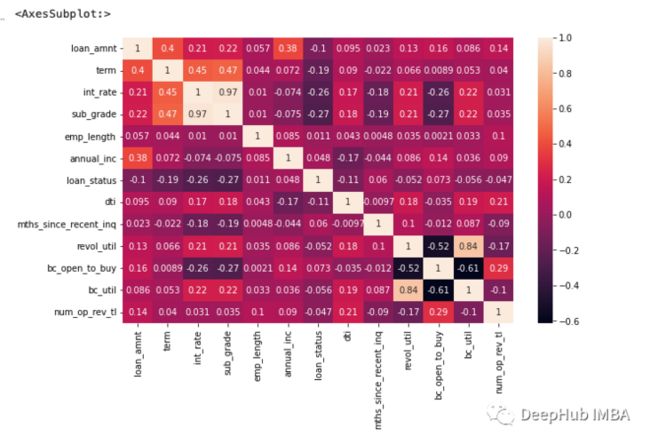
如何理解相关矩阵:相关性范围从+1到-1,其中:
- 零相关表示变量之间没有关系;
- 相关性为-1表示完全负相关,这意味着当一个变量上升时,另一个变量下降;
- 相关性为+1表示完全正相关,这意味着两个变量一起朝同一个方向移动。
上图可以观察到以下高度相关的特征:
- 客户信息相关的特征:bc_open_to_buy / num_op_rev_tl。这两个特征都与循环账户和银行卡有关,因此它们高度相关。为了避免多协同问题,去掉初始模型中的bc_open_to_buy特性。revol_util / bc_util。也是一个类似的情况,可以删除bc_util特性。
- 贷款信息特性:Int_rate和grade是基于借贷专有模型的sub_grade的衍生品;因此它们是高度相关的;我们把这些删除。这里的sub_grade和loan_amount也是相关的,但关联度较低,可以保留它们。
loans.drop(["bc_util", "bc_open_to_buy","int_rate", "grade"], axis = 1, inplace = True)第三步:找出特征与目标变量之间的相关性
我们希望能够找到与目标变量(在本例中为loan_status)高度相关的特性。这里将回顾上面介绍的两种流行的方法:
基于过滤的方法
相关矩阵可以帮助我们识别高度相关的特征。pandas_profiling生成分析报告可能需要时间,因此了解绘制相关矩阵的其他技术是必要的。下面是两种可选方法:
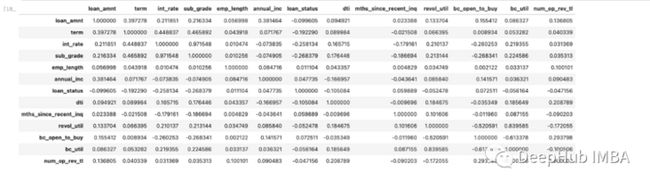
使用pandas自带的corr函数
loans_cor=loan.corr()
loans_cor使用seaborn热点图
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(10,6))
sns.heatmap(loans_cor, annot=True)我们可以观察到以下高度相关的特征:sub_grade, term, loan_amnt, dti, emp_length, annual_inc与loan_status。这可以让我们知道哪些特性是重要的。
包装器方法
包装器的方法是一种选择特征的更自动化的方式,我们将使用内置函数 SequentialFeatureSelector()实现前向选择,该函数是 mlxtend 库的一部分。此函数具有不同的特征选择技术。
SequentialFeatureSelector() 有 11 个参数,您可以调整这些参数以获得最佳结果。我们这里将调整以下参数:
- Estimator——核心使用的算法;在这个们的例子中将使用 LogisticRegression() 算法;
- k_features — 希望算法选择为最佳特征的特征数(默认为 1)。它应该小于数据集的所有特征数总和。mlxtend 包还提供了“best”参数,其中选择器返回最佳交叉验证性能。因此,与其猜测需要返回多少特征,不如应用“best”;
- Forward 和 floating 参数来标识包装器方法:例如,对于我们的前向选择,它将是forward = True,而floating = False;
- Scoring :指定了评估标准:使用 sklearn 评分指标“precision”。对于分类器,因为数据集是不平衡的。我们还可以使用 f1、precision、recall、roc_auc 等用于分类任务的指标和 r2 、mean_absolute_error、mean_squared_error/neg_mean_squared_error、median_absolute_error 用于回归任务的指标;
- cv——交叉验证,默认为5。
现在让我们将上面定义的特征选择器应用到的数据集中。
对于给定的数据将尝试一个非常常见的算法-逻辑回归序列特征选择器。Loan_status将被用作预测的标签以查找预测的依赖项:
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.preprocessing import MinMaxScaler
X = loans.drop('loan_status', axis=1)
y = loans[['loan_status']]
y = y.values.ravel() X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42, stratify=y)
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)下一步是我们将使用SequentialFeatureSelector来寻找“最佳”特征:
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
sfs = SFS(LogisticRegression(),
k_features='best',
forward=True,
floating=False,
scoring = 'precision',
cv = 0)将上面的特征选择器应用到我们的数据:
sfs.fit(X, y)
sfs.k_feature_names_返回并查看ML任务应该使用的最佳特性:
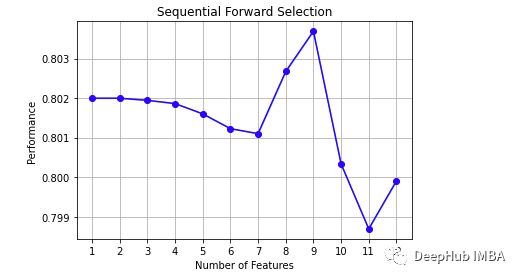
通过比较每个训练步骤中的性能和特征数量来了解选择过程。还可以看到所选择的模型度量在迭代步骤中不会发生很大的变化。
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
import matplotlib.pyplot as plt
fig1 = plot_sfs(sfs.get_metric_dict(), kind='std_dev') plt.title('Sequential Forward Selection')
plt.grid()
plt.show()可以看到不同特征的指标表现
总结
在本文中,我们介绍了特征选择技术的基本原理,这对理解重要特征和结果变量之间的相关性是非常关键的。本篇文章的代码:https://avoid.overfit.cn/post/6f2a58732ffa42ba8dffa6db78c5ebc0
作者:Maria Gusarova