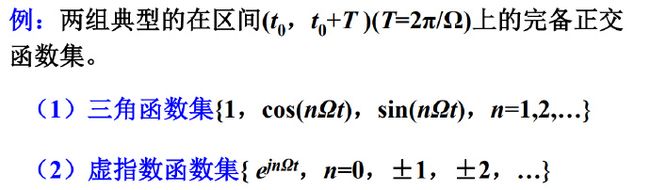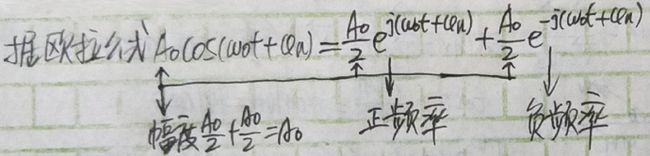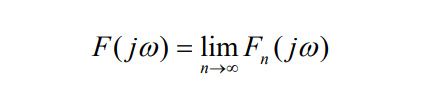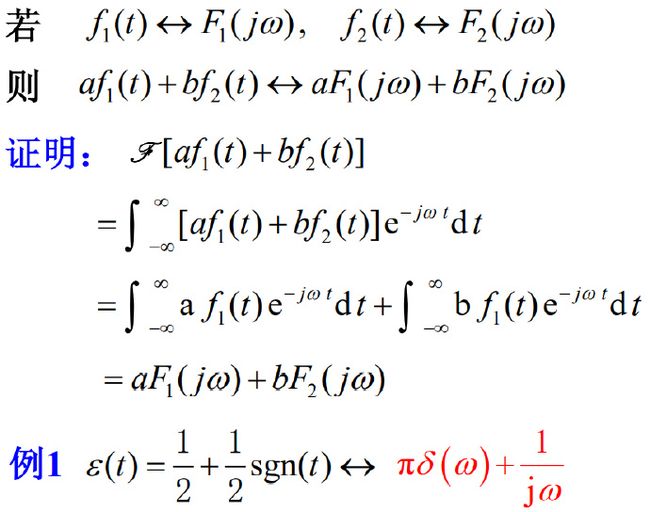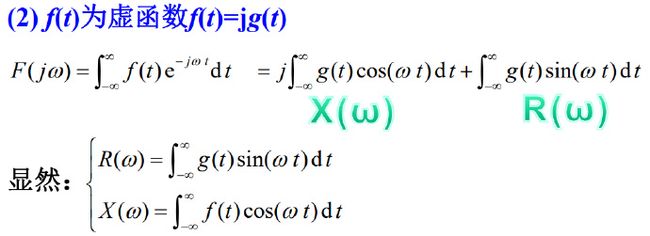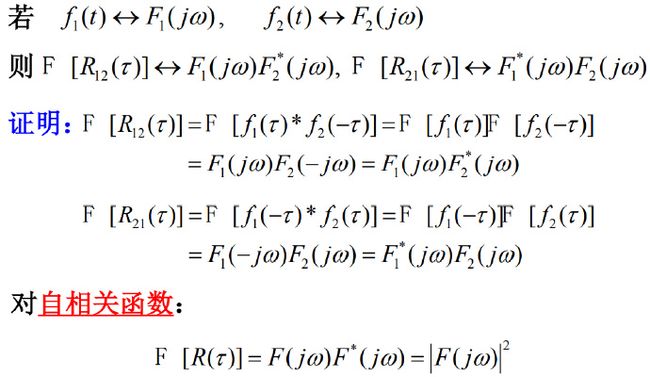信号与系统3-傅里叶变换与频域分析

目录：

四、傅里叶变换

1、引言

2、周期信号傅里叶级数分析

1）三角函数形式的傅里叶级数

（1）矢量的正交分解   （2）信号的正交分解   （3）傅里叶级数形式

（4）狄里克利（Dirichlet）条件   （5）吉布斯现象   （6）周期信号波形对称性和谐波特性

2）指数函数形式的傅里叶级数

3）两种傅里叶级数展开形式的关系

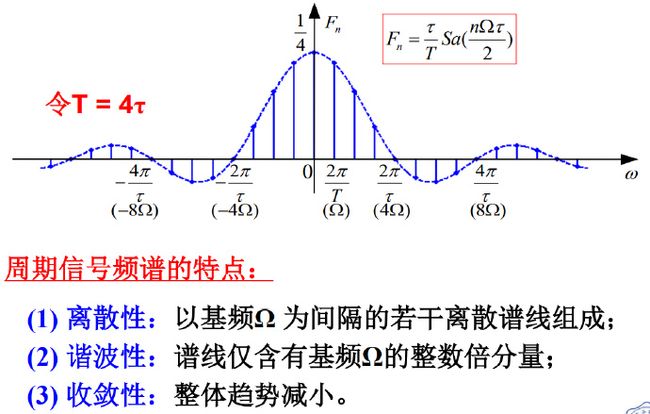
4）周期信号的频谱

5）单边谱和双边谱的关系

6）周期信号频谱的特点

7）周期信号的功率

3、傅里叶变换

1）非周期信号的频谱   2）傅里叶变换

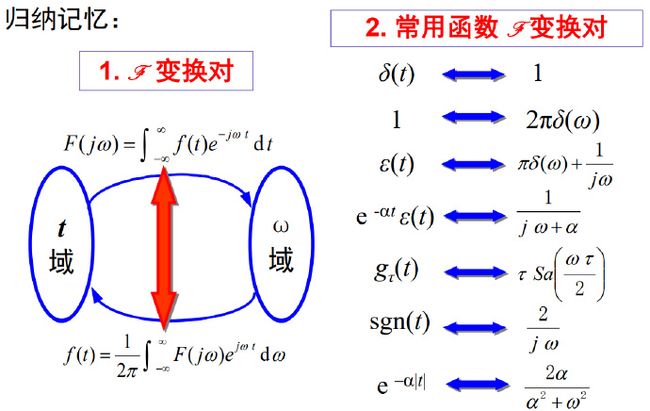
4、常用信号的傅里叶变换

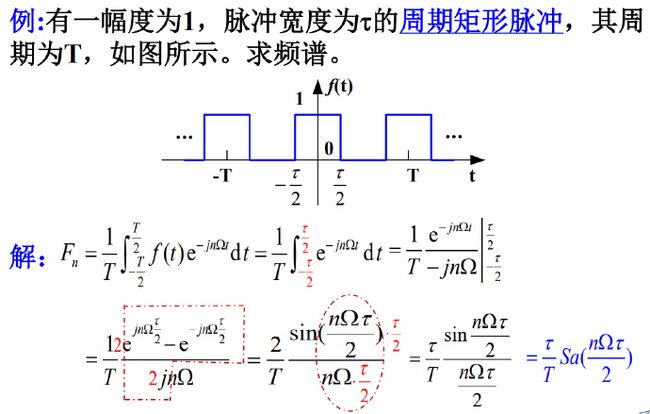
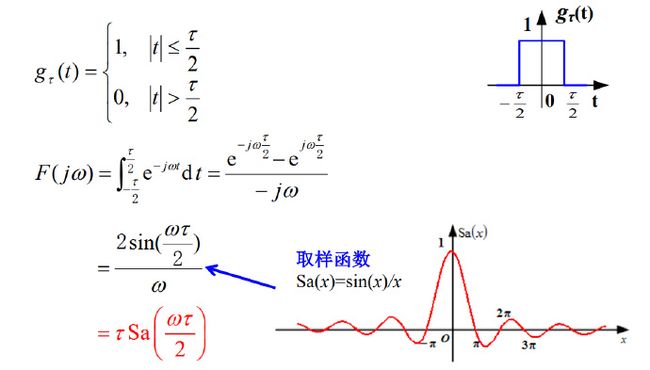
1）单边指数函数  2）双边指数函数   3）门函数(矩形脉冲)   4）冲激函数δ(t)、δ´(t)、 δ(n)(t)

5）常数“1”   6）符号函数   7）阶跃函数 ε(t)   8）总结

5、傅里叶变换的基本性质

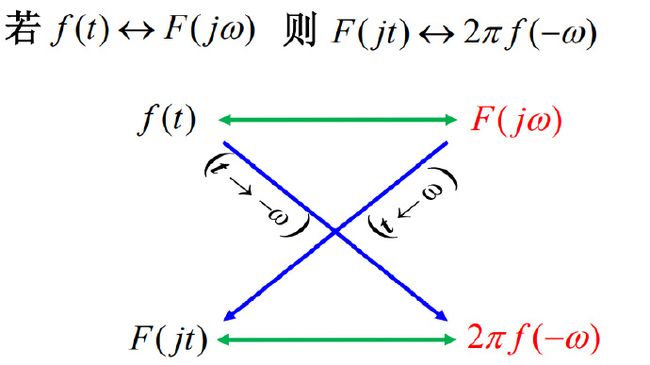
1）线性性质   2）奇偶性   3）对称性   4）尺度变换   5）时移特性   6）频移特性

7）卷积定理   8）时域微积分特性   9）频域微积分特性   10）相关定理

6、能量谱和功率谱

1）能量谱   2）功率谱

7、周期信号的傅里叶变换

1）周期信号的傅里叶变换   2）周期信号傅里叶级数与傅里叶变换的关系

8、LTI系统的频域分析

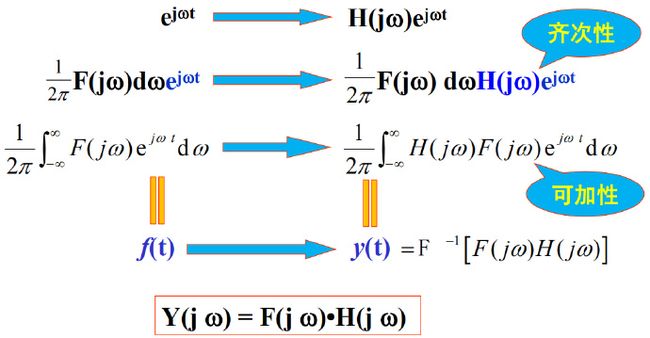
1）基本信号ejωt作用于LTI系统的响应   2）一般信号f(t)作用于LTI系统的响应

3）傅里叶变换分析法   4）傅里叶级数分析法   5）频率响应函数

9、无失真传输与理想低通滤波器

1）无失真传输   2）理想低通滤波器   3）物理可实现系统的条件

10、取样定理

1）信号的取样   2）取样定理（时域）   3）取样定理（频域）

附录1、参考

1、傅立叶变换的直观解释

2、微积分基础2-积分篇

3、微积分基础3-微分方程与向量

4、数学-三角函数

5、欧拉公式

-----------------------------------------------------------------------------------------------------------------

四、傅里叶变换

1、引言

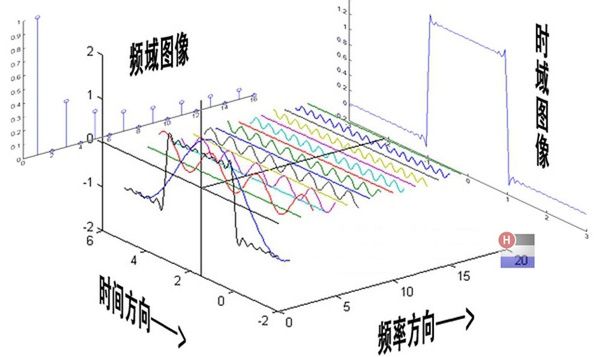
频域分析：傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产生的，也称为傅里叶分析（频域分析）。将信号进行正交分解，即分解为三角函数或复指数函数的组合。

频率分析将时间变量变换成频率变量，揭示了信号内在的频率特性以及信号时间特性与其频率特性之间的密切关系，从而导出了信号频谱带宽以及滤波、调制和频分复用等。

任何一个函数，都可以用很多个正弦波叠加的方式仿造一个一模一样的函数。仿造出来之后，再把这么多正弦波按照频率依次排开。

所以很多在时域看似不可能做到的数学操作，在频域却很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分，这在工程上称为滤波，是信号处理最重要的概念之一，只有在频域才能轻松的做到。

求解微分方程是一件相当麻烦的事情。因为除了要计算加减乘除，还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法，大学数学瞬间变小学算术。

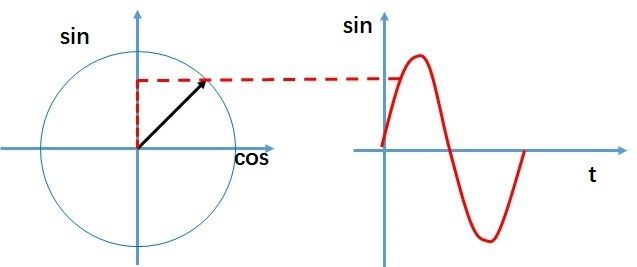
高中时都学过什么是余弦和正弦。它们将直角三角形的一个角度与两个边长的比值联系起来。另一种理解方式是：余弦和正弦分别是围绕单位圆运动的一个点的x和y坐标。它们是人们能想到的最简单的周期函数之一。

余弦和正弦作为绕单位圆运动的点的坐标(此点可以用虚数表示)，由这两个函数组成的和，可以表示任何数学函数，这一事实让人惊讶。

P点在四个象限变动：

-----------------------------------------------------------

2、周期信号傅里叶级数分析

1）三角函数形式的傅里叶级数

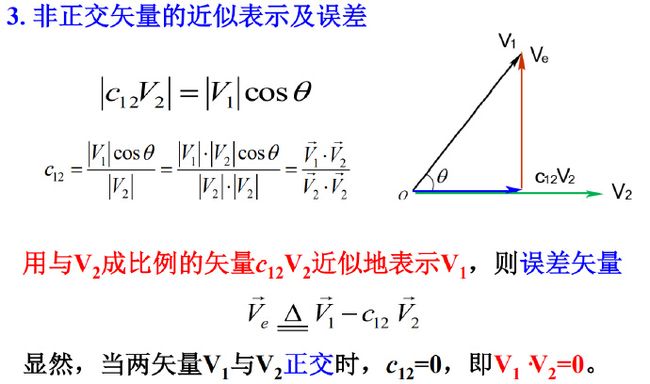
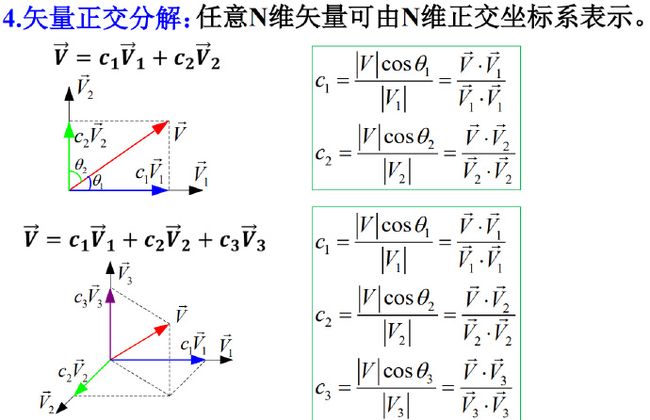
（1）矢量的正交分解

-----------------

（2）信号的正交分解

对于两个连续函数来说，应该如何表示正交呢？

函数在某个区间内部有无穷多个点，无法直接套用内积公式。但可以借鉴积分思想，将函数在一段连续区间分割成一份一份，这样每一份的取值合起来就可以组成一个向量，于是可用向量的内积表示两个函数是否正交。如下图：

当分割的区间无限小时，向量变成无限维，于是向量的内积就可以用积分来替代了。所以两个函数的正交其实可以用积分来表示。

对于sin4x和sin2x，在一个周期内，处于X轴上下方的面积相等，所以这两个函数的积分为0，也就是互相正交。

 

积分的两个函数相同，都是sin4x，这时积分结果都在X轴上方，积分大于0，也就是不正交。

如图3.2.1的∫cosx*sinx*dx、∫cosx*cosx*dx、∫sinx*sinx*dx的任意两个一个周期内做积分在m≠n时值为零，即互相正交。

图3.2.1

图3.2.2

关于三角函数移步：数学-三角函数。

-----------------

（3）傅里叶级数形式

考虑到一个函数可以展开成一个多项式的和，可惜多项式并不能直观的表示周期函数，由于正余弦函数是周期函数，可以考虑任意一个周期函数能否表示成为一系列正余弦函数的和。假设可以，不失一般性，于是得到： 

    f(t)= A0+∑(n=1,∞) Ansin(nωt+Φn)

将后面的正弦函数展开：

    Ansin(nωt+Φn)=AnsinΦncos(nωt)+AncosΦnsin(nωt)

令 a0 =A0，an = AnsinΦn，bn=AncosΦn，可得图3.2.3的(1)式。

图3.2.3 a0、an、bn另可参看高等数学(上海交大-乐经良)

-----------------

（4）狄里克利（Dirichlet）条件

函数1个周期内只能存在有限个间断点与有限个极值；在1个周期绝对可积。

-----------------

（5）吉布斯现象

用有限项傅里叶级数表示间断点的信号时，在间断点附近不可避免的出现振荡和超量。超量的幅度不会随所取项数的增加而减小，只是随着项数的增多，振荡频率变高，并向间断点处压缩，从而使它所占有的能量减小。

-----------------

（6）周期信号波形对称性和谐波特性

--------------------------------

2）指数函数形式的傅里叶级数

-----------------

举例：

 

--------------------------------

3）两种傅里叶级数展开形式的关系

--------------------------------

4）周期信号的频谱

--------------------------------

5）单边谱和双边谱的关系

帕斯瓦尔等式：

--------------------------------

6）周期信号频谱的特点

 

--------------------------------

7）周期信号的功率

 

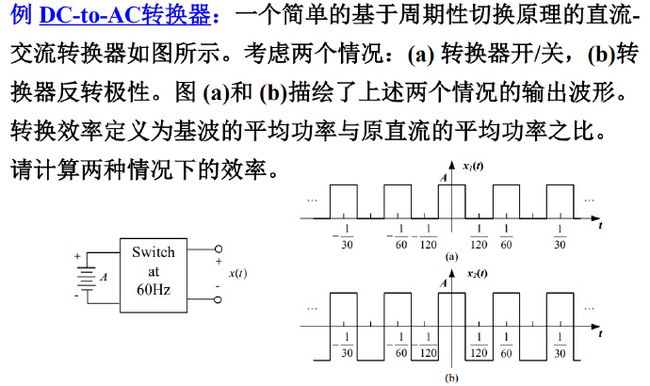
应用案例：DC-to-AC转换器

-----------------------------------------------------------

3、傅里叶变换

1）非周期信号的频谱

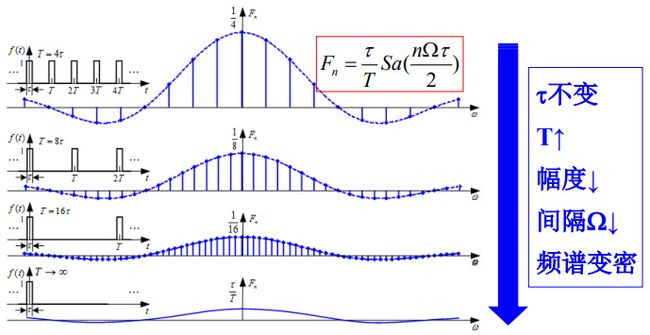
非周期信号可以看作周期为无穷大的周期信号。

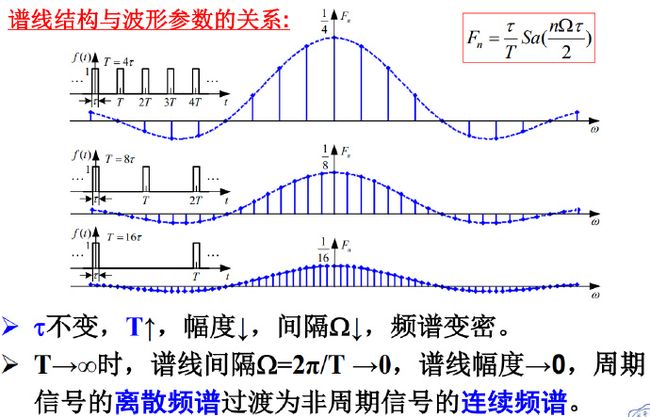
T→∞时，f(t)：周期信号→非周期信号；谱线间隔Ω=2π/T→0，谱线幅度τ/T→0，周期信号的离散频谱过渡为非周期信号的连续频谱。

注意：虽然各频率分量的幅度趋近于无穷小，但无穷小量之间仍有相对大小差别。故引入频谱密度函数，把Fn放大无穷大倍即乘以T。

 

F(jω)称为频谱密度函数，简称频谱密度或频谱(虽然简称为频谱，但也是经过放大无穷倍后的频谱)，单位频率上的频谱。

F(jω)与Fn是不在一个层次上的，Fn是实际频谱的强度，F(jω)是放大无穷倍后强度，但二者都反映了频谱的大小。

--------------------------------

2）傅里叶变换

-----------------------------------------------------------

4、常用信号的傅里叶变换

1）单边指数函数

--------------------------------

2）双边指数函数

--------------------------------

3）门函数(矩形脉冲)

--------------------------------

4）冲激函数δ(t)、δ´(t)、 δ(n)(t)

--------------------------------

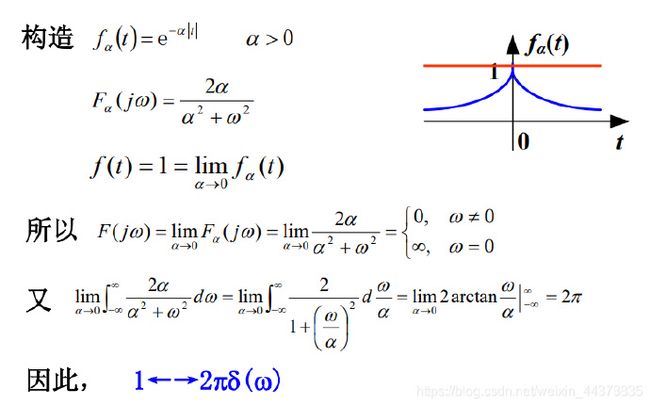
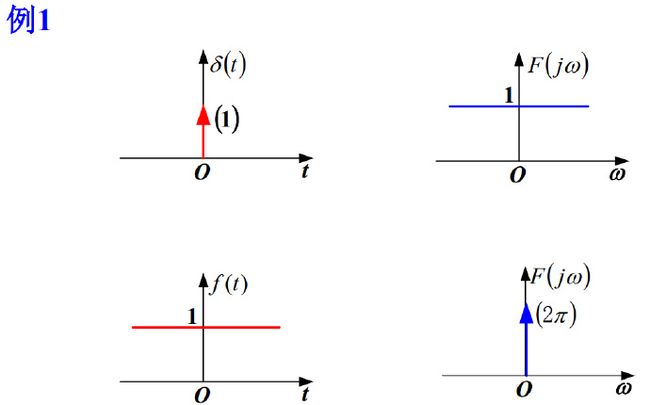
5）常数“1”

有些函数(如1，u(t)等)不满足绝对可积这一充分条件，直接用定义式不易求解。可构造一函数序列{undefinedfn(t)}逼近f(t) ，即

而fn(t)满足绝对可积条件，并且{undefinedfn(t)}的傅里叶变换所形成的序列{undefinedFn(jω)}是极限收敛的。则f(t)的傅里叶变换F(jω)为

这样定义的傅里叶变换也称为广义傅里叶变换。

e^(-αt)，α趋于无穷，其值为1。

F(jω)在ω=0时无穷大，ω = 0时为0，故F(jω)是一个冲激函数，通过求[−∞，∞ ]的积分可以求得其面积为2π，而δ(ω)面积为1，故F(jω)=2πδ(ω)。

另一种求法： δ(ω) 代入反变换定义式，有

--------------------------------

6）符号函数

--------------------------------

7）阶跃函数 ε(t)

--------------------------------

8）总结

-----------------------------------------------------------

5、傅里叶变换的基本性质

1）线性性质

--------------------------------

2）奇偶性

--------------------------------

3）对称性质

--------------------------------

4）尺度变换

--------------------------------

5）时移特性

 

--------------------------------

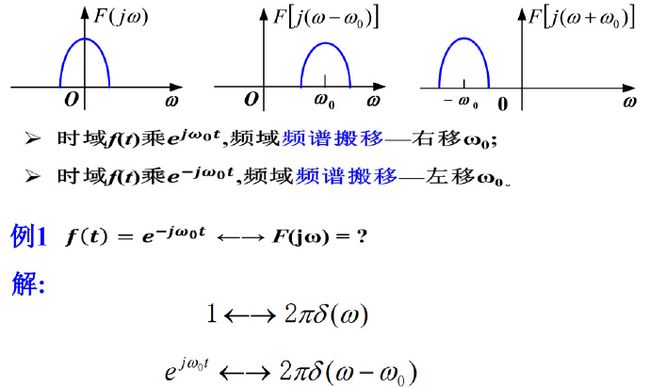
6）频移特性

--------------------------------

7）卷积定理

--------------------------------

8）时域微积分特性

--------------------------------

9）频域微积分特性

--------------------------------

10）相关定理

-----------------------------------------------------------

6、能量谱和功率谱

1）能量谱

 

--------------------------------

2）功率谱

 

 

白噪声功率谱密度的估计

对于随机信号，由于不能直接用频谱表示，但是可以利用自相关函数求其功率谱密度，借助功率谱描述

随机信号的频域特性。白噪声是一种典型的随机信号。

白噪声(white noise)是指功率谱密度在整个频域内均匀分布的随机噪声。

通信中的白噪声主要包含三类：

（1）无源器件,如电阻、馈线等类导体中电子布朗运动引起的热噪声；

（2）有源器件,如真空电子管和半导体器件中由于电子发射

的不均匀性引起的散粒噪声；

（3）宇宙天体辐射波对接收机形成的宇宙噪声。其中前两类是主要的。

例：利用MATLAB产生白噪声并进行功率谱密度估计。

%生成高斯白噪声序列

randn('state',0)

NFFT=1024; %NFFT为取样点数

Fs=10000; %Fs为取样频率

t=(0:NFFT-1)/Fs; %时间

y=randn(NFFT,1); %产生高斯白噪声，2*pi为其功率。

figure(1);

subplot(3,1,1); plot(t,y); grid on; title('白噪声波形');

%计算白噪声的自相关函数

[cory,lags]=xcorr(y,200,'unbiased'); %自相关函数(无偏差的)， cory为自相关函数，

lag为自相关函数的长度。

subplot(3,1,2);

plot(lags,cory); grid on; title('白噪声相关函数');

%估计功率谱密度

f=fft(cory); %对自相关系数进行傅里叶变换：即功率谱密度。

k=abs(f); % k是cory傅里叶变换的幅值。

fl=(0:length(k)-1)*Fs/length(k); %fl为fc的长度。

subplot(3,1,3)

plot(fl,k); grid on; title('白噪声功率谱'); 

-----------------------------------------------------------

7、周期信号的傅里叶变换

1）周期信号的傅里叶变换

--------------------------------

2）周期信号傅里叶级数与傅里叶变换的关系

-----------------------------------------------------------

8、LTI系统的频域分析

思考问题：

* 一般信号的分解？傅里叶级数？傅里叶变换？

* 基本信号的响应？e jnΩt？ejωt？

* 一般信号的响应？傅里叶级数？傅里叶变换？

* 频域分析？数学工具？原理？步骤？优缺点？

--------------------------------

2）一般信号f(t)作用于LTI系统的响应

--------------------------------

3）傅里叶变换分析法

--------------------------------

4）傅里叶级数分析法

--------------------------------

5）频率响应函数

-----------------------------------------------------------

9、无失真传输与理想低通滤波器

1）无失真传输

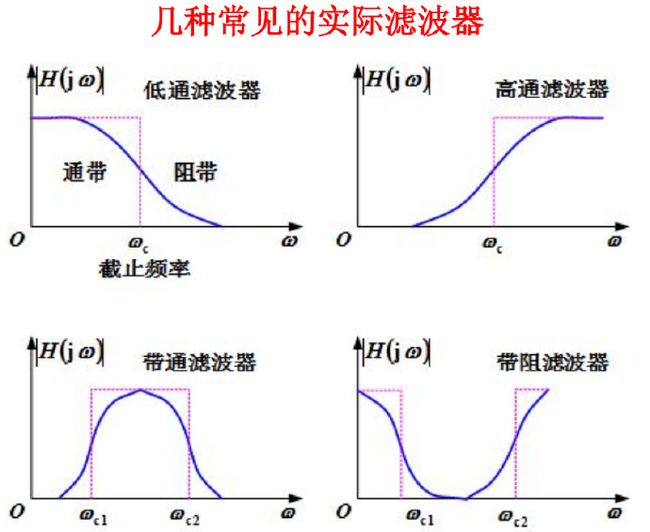
系统对于信号的作用大体可分为两类：一类是信号的传输，一类是滤波。传输要求信号尽量不失真，而滤波则要求滤去或削弱不需要的成分，必然伴随着失真。

--------------------------------

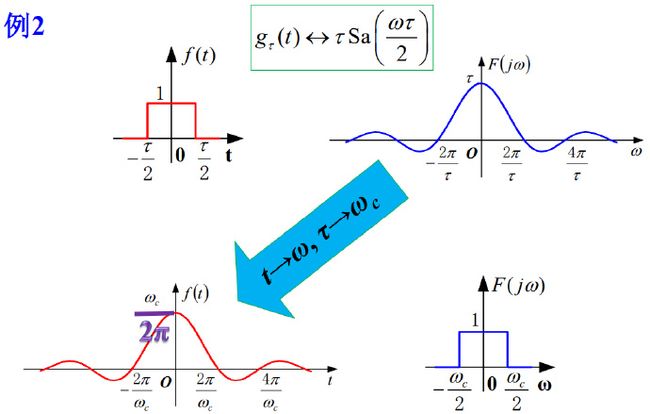
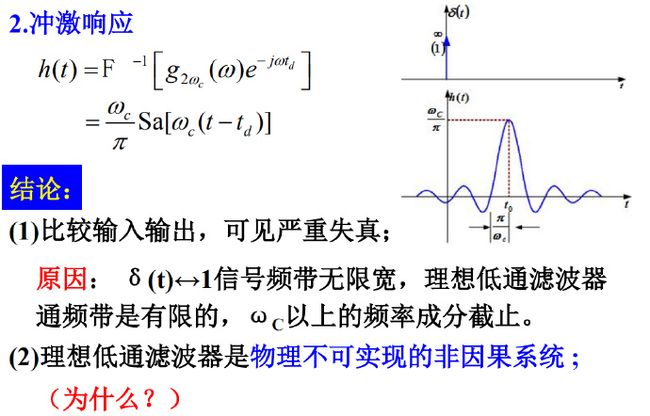
2）理想低通滤波器

--------------------------------

3）物理可实现系统的条件

说明：

(1)物理可实现系统时域特性表明，响应不应在激励作用之前出现；

(2)对于物理可实现系统,可以允许H(jω) 特性在某些不连续的频率点上为0，但不允许在一个有限频带内为0。按此原理，理想低通、理想高通、理想带通、理想带阻等理想滤波器都是不可实现的；

(3)佩利-维纳准则要求可实现的幅度特性其总的衰减不能过于迅速；

(4)佩利-维纳准则是系统物理可实现的必要条件，而不是充分条件。

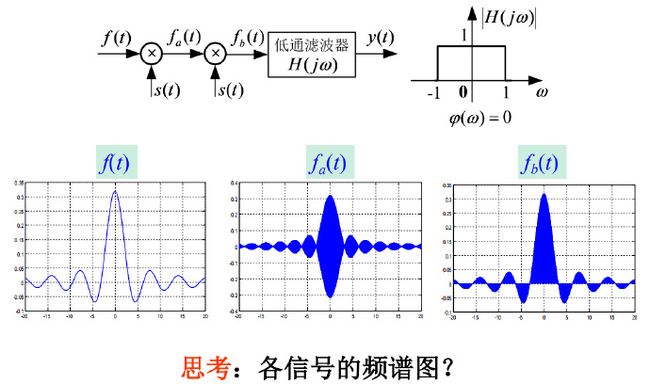
案例：二次抑制载波振幅调制接收系统

-----------------------------------------------------------

10、取样定理

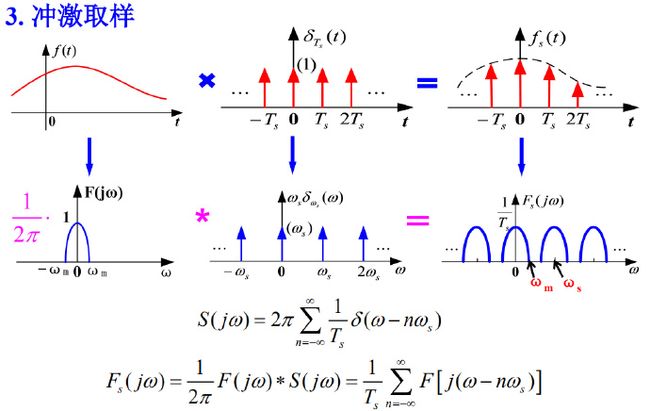
1）信号的取样

--------------------------------

2）取样定理（时域）

--------------------------------

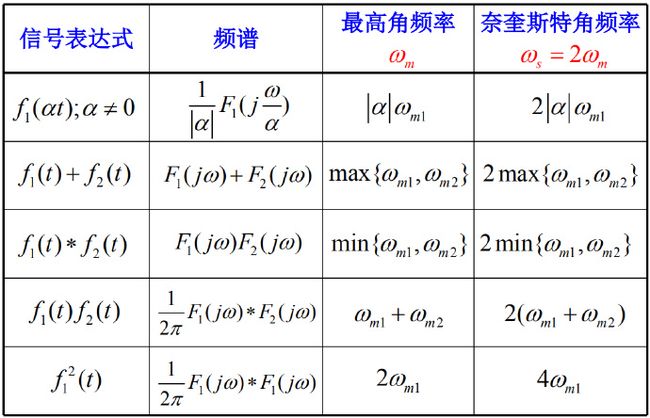
3）取样定理（频域）

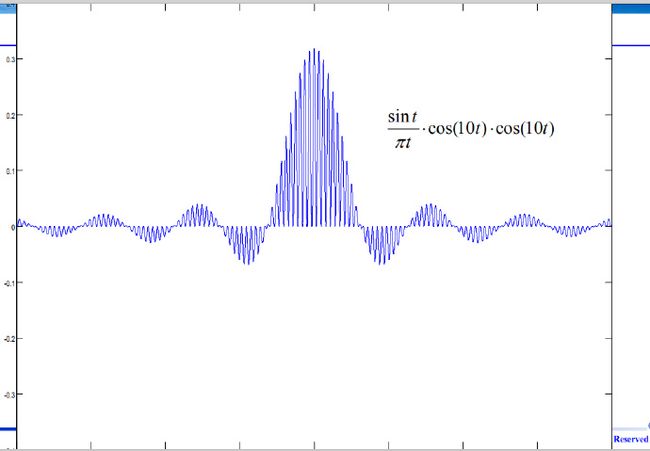
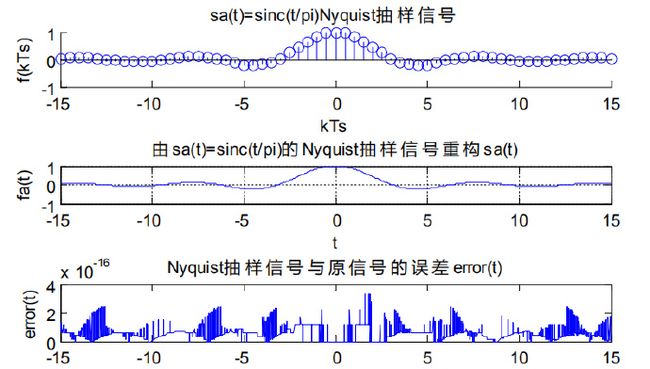
Matlab实现Sa信号的采样和恢复

例：信号Sa(t)作为被采样信号，信号带宽B=1, 采样频率ωs=2B，此频率下的采样为Nyquist采样，对采样及恢复过程用Matlab进行仿真。

解：B=1; %信号带宽

wc=B; %滤波器截止频率

Ts=pi/B; %采样间隔

ws=2*pi/Ts %采样角频率

N=100; %滤波器时域采样点数

n=-N:N;

nTs=n.*Ts; %采样数据的采样时间

fs=sinc(nTs/pi); %函数的采样点

Dt=0.005; %恢复信号的采样间隔

t=-15:Dt:15; %恢复信号的范围

fa=fs*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));

%信号重构

error=abs(fa-sinc(t/pi)); %求重构信号与原信号的归一化误差

从误差图形中可以看到，用采样信号恢复的信号与原始信号的误差是极小的，而且这种误差来自于计算过程的数值计算误差。表明:对一个信号进行Nyquist采样后，能够无误差地从采样信号中恢复出原信号。

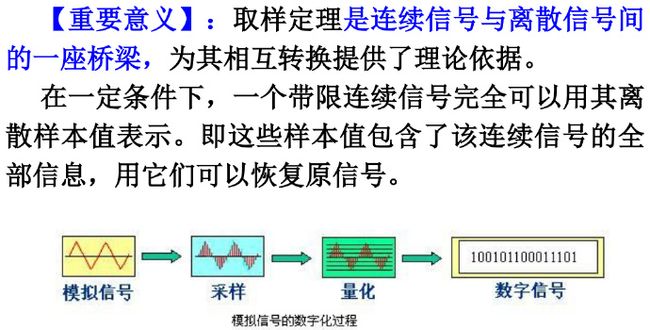
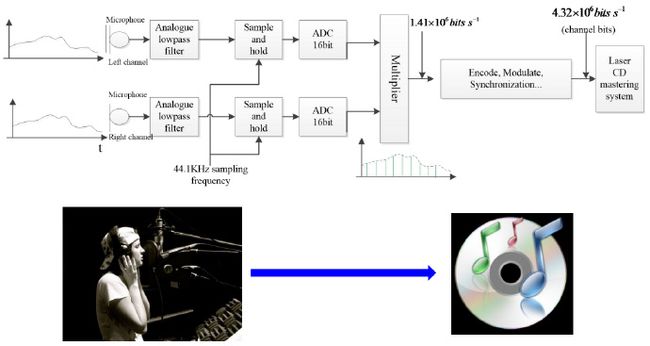
应用案例：CD数字录音系统

CD数字录音系统:

(1) 麦克风采集声音信号，并输出模拟电信号，即麦克风实现声电转换的功能;

(2) 模拟低通滤波器对来自麦克风的模拟信号进行滤波，滤除高频噪声;

(3) 为了便于后续的数字处理，需要对模拟信号进行采样保持;

(4) 将模拟信号进行采样以后得到的信号一般称为离散信号。离散信号需要进行模数转换(Analog Digital Convert, ADC)，得到数

字信号，这个过程称为量化；

(5) 将数字信号编码、调制、同步处理后刻入CD。

关键问题: CD系统如何选择采样率？

CD系统的设计目标是期望能够记录下人类听觉系统所能听到的所有声音 ，其频率范围是20Hz～20KHz；由时域采样定理知道，采样频率要达到原始信号的2倍。这就是图中采样率是44.1KHz的原因，采用44.1KHz而不是40KHz是为了留有一定余量。当然，采样频率越大越有利于完美再现原始信号，但过高的采样率将导致数据量过大。

-----------------------------------------------------------------------------------------------------------------

附录1、参考

1、傅立叶变换的直观解释

2、微积分基础2-积分篇

3、微积分基础3-微分方程与向量

4、数学-三角函数

5、欧拉公式

-----------------------------------------------------------------------------------------------------------------