pytorch基础（二）

1、 nn.Softmax(dim)

新建一个2x2大小的张量，一行理解成一个样本经过前面网络计算后的输出（1x2），则batch_size是2

import numpy as np                
import torch                
import torch.nn as nn                
a = np.array([[1.5, 6.7],[6.8, 3.4]])                
b = torch.from_numpy(a)
f = nn.Softmax(dim = 0)
c = f(b)

输出结果：

 tensor([[0.0050, 0.9644], [0.9950, 0.0356]], dtype=torch.float64)

可以发现，是每一列和为1.

 f = nn.Softmax(dim = 1)

输出结果可以得到：

tensor([[0.0055, 0.9945],  [0.9677, 0.0323]], dtype=torch.float64)

可以发现是每一行和为1
当nn.Softmax的输入是一个二维张量时，其参数dim = 0，是让列之和为1；dim = 1，是让行之和为1。
nn.Softmax的输入是三维张量时，dim的取值就变成了0，1，2

a = np.array([[[1.5, 6.7, 2.4],

              [6.8, 3.4, 9.3]],

              [[3.1, 6.5, 1.9],

              [8.9, 1.2, 2.5]]])

a换成一个三维数组，大小是2x2x3，可以看成是2个2x3大小的输入
定义Softmax函数的dim为0

tensor([[[0.1680, 0.5498, 0.6225], 
         [0.1091, 0.9002, 0.9989]],  
        [[0.8320, 0.4502, 0.3775],   
         [0.8909, 0.0998, 0.0011]]], dtype=torch.float64)

发现其中；

让两个2x3数据的对应位置和为1.
dim=1，结果是：

tensor([[[0.0050, 0.9644, 0.0010],        
         [0.9950, 0.0356, 0.9990]],        
        [[0.0030, 0.9950, 0.3543],         
         [0.9970, 0.0050, 0.6457]]], dtype=torch.float64)

是让张量每个2x3数据自己的列之和为1.
使dim=2，就是让张量每个2x3数据自己的行之和为1.
当dim=0时， 是对每一维度相同位置的数值进行softmax运算，和为1
当dim=1时， 是对某一维度的列进行softmax运算，和为1
当dim=2或dim=-1时， 是对某一维度的行进行softmax运算，和为1

2、torch.bmm()函数

计算两个tensor的矩阵乘法，torch.bmm(a,b),tensor a 的size为(b,h,w),tensor b的size为(b,w,m) 也就是说两个tensor的第一维是相等的，然后第一个数组的第三维和第二个数组的第二维度要求一样，对于剩下的则不做要求，输出维度 （b,h,m）

3、permute的用法

将tensor的维度换位。

import torch
import numpy as np
a=np.array([[[1,2,3],[4,5,6]]])
unpermuted=torch.tensor(a)
print(unpermuted.size()) # ——> torch.Size([1, 2, 3])
permuted=unpermuted.permute(2,0,1)
print(permuted.size()) # ——> torch.Size([3, 1, 2])

函数permute（1，3，2）可以把Tensor([[[1,2,3],[4,5,6]]]) 转换成

tensor([[[1., 4.],
         [2., 5.],
         [3., 6.]]])

torch.from_numpy()

torch.from_numpy()方法把数组转换成张量，且二者共享内存，对张量进行修改比如重新赋值，那么原始数组也会相应发生改变。

>>> a = numpy.array([1, 2, 3])
>>> t = torch.from_numpy(a)
>>> t
tensor([ 1, 2, 3])
>>> t[0] = -1
>>> a
array([-1, 2, 3])

np.triu()和np.tril()的用法

a=np.array([[1,2],[3,4]])
print(np.tril(a))#生成下三角
print(np.triu(a))#生成上三角

masked_fill_(mask, value)

掩码操作
用value填充tensor中与mask中值为1位置相对应的元素。mask的形状必须与要填充的tensor形状一致。

a = torch.randn(5,6)

x = [5,4,3,2,1]
mask = torch.zeros(5,6,dtype=torch.float)
for e_id, src_len in enumerate(x):
    mask[e_id, src_len:] = 1
mask = mask.to(device = 'cpu')
print(mask)
a.data.masked_fill_(mask.byte(),-float('inf'))
print(a)
----------------------------输出
tensor([[0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 1., 1.],
        [0., 0., 0., 1., 1., 1.],
        [0., 0., 1., 1., 1., 1.],
        [0., 1., 1., 1., 1., 1.]])
tensor([[-0.1053, -0.0352,  1.4759,  0.8849, -0.7233,    -inf],
        [-0.0529,  0.6663, -0.1082, -0.7243,    -inf,    -inf],
        [-0.0364, -1.0657,  0.8359,    -inf,    -inf,    -inf],
        [ 1.4160,  1.1594,    -inf,    -inf,    -inf,    -inf],
        [ 0.4163,    -inf,    -inf,    -inf,    -inf,    -inf]])

pytorch中两个张量的乘法可以分为两种：
两个张量对应元素相乘，在PyTorch中可以通过torch.mul函数（或*运算符）实现；
两个张量矩阵相乘，在PyTorch中可以通过torch.matmul函数实现；

torch.matmul(input, other) → Tensor

计算两个张量input和other的矩阵乘积
**【注意】：**matmul函数没有强制规定维度和大小，可以用利用广播机制进行不同维度的相乘操作。

两个一维向量的乘积运算

import torch
x = torch.tensor([1,2])
y = torch.tensor([3,4])
print(x,y)
print(torch.matmul(x,y),torch.matmul(x,y).size())

输出结果：

tensor([1, 2]) tensor([3, 4])
tensor(11) torch.Size([])

两个二维矩阵的乘积运算

若两个tensor都是二维的，则返回两个矩阵的矩阵相乘结果：

import torch
x = torch.tensor([[1,2],[3,4]])
y = torch.tensor([[5,6,7],[8,9,10]])
print(torch.matmul(x,y),torch.matmul(x,y).size())

运行结果：

tensor([[21, 24, 27],[47, 54, 61]]) torch.Size([2, 3])

一个一维向量和一个二维矩阵的乘积运算

若input为一维，other为二维，则先将input的一维向量扩充到二维（维数前面插入长度为1的新维度），然后进行矩阵乘积，得到结果后再将此维度去掉，得到的与input的维度相同。

import torch
x = torch.tensor([1,2])
y = torch.tensor([[5,6,7],[8,9,10]])
print(torch.matmul(x,y),torch.matmul(x,y).size())

运行结果：

tensor([21, 24, 27]) torch.Size([3])

一个二维矩阵和一个一维向量的乘积运算

若input为二维，other为一维，则先将other的一维向量扩充到二维（维数后面插入长度为1的新维度），然后进行矩阵乘积，得到结果后再将此维度去掉，得到的与other的维度相同。

import torch
x = torch.tensor([[1,2,3],[4,5,6]])
y = torch.tensor([7,8,9])
print(torch.matmul(x,y),'\n',torch.matmul(x,y).size())

运行结果：

运行结果：
tensor([ 50, 122])
torch.Size([2])

将y从一维扩展为二维，([7,7,7]，[8,8,8]，[9,9,9])，然后进行相乘，
得到结果后再将添加的 维度取消。

nn.Linear()：

用于设置网络中的全连接层，需要注意的是全连接层的输入与输出都是二维张量

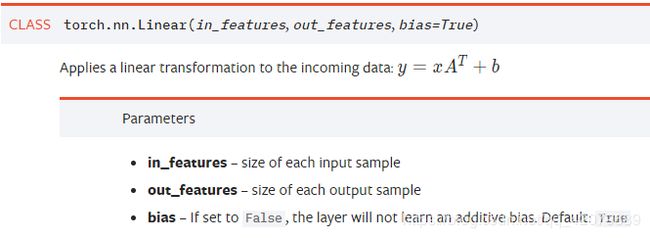
in_features指的是输入的二维张量的大小，即输入的[batch_size, size]中的size。
out_features指的是输出的二维张量的大小，即输出的二维张量的形状为[batch_size，output_size]，当然，它也代表了该全连接层的神经元个数。
从输入输出的张量的shape角度来理解，相当于一个输入为[batch_size, in_features]的张量变换成了[batch_size, out_features]的输出张量。

import torch as t
from torch import nn

# in_features由输入张量的形状决定，out_features则决定了输出张量的形状 
connected_layer = nn.Linear(in_features = 64*64*3, out_features = 1)

# 假定输入的图像形状为[64,64,3]
input = t.randn(1,64,64,3)

# 将四维张量转换为二维张量之后，才能作为全连接层的输入
input = input.view(1,64*64*3)
print(input.shape)
output = connected_layer(input) # 调用全连接层
print(output.shape)