WebGL编程指南笔记-第四章 高级变换与动画基础
第四章 高级变换与动画基础
本章内容
第三章中学了利用缓冲区对象绘制三角形，图形变换的原理，利用矩阵简化变换操作等。
本章中进一步研究变换矩阵，在此基础制作一些简单的动画效果，具体内容包括：
- 学习使用一个矩阵变换库，库中封装了矩阵运算的数学细节
- 快速上手矩阵库，对图形进行复合变换
- 利用矩阵库，实现简单的动画效果。
本章内容是复杂的WebGL程序的基础。
平移，然后旋转
上一张最后的综合练习中，已经通过变换矩阵实现了平移和旋转，通过综合练习切入矩阵函数库的学习。
矩阵变换库
先举个例，在opengl中glTranslate()函数并传入x, y, z上的平移距离，就可以创建一个平移矩阵
但是在webgl中，没有提供类似的函数库。接下来开始学习使用书中提供的矩阵函数库
示例程序（RotatedTriangle_Matrix4.js）
示例代码：RotatedTriangle_Matrix4.js
旧的创建方式，我们要自己去编写变换矩阵，位于代码的29～40行，和52行
新的创建方式，使用书中提供的Matrix库，位于代码的42～46行，和54行
在新的创建方式中，通过简单三句代码就可以创建好变换矩阵和将数据传入着色器
// 通过new Matrix4()创建一个Matrix4类型的对象
var xformMatrix = new Matrix4();
// 通过setRotate()把自身设为计算出的旋转矩阵
// 函数的接收的参数分别为：旋转角(角度制，库的内部会转为弧度制)，旋转轴x, y, z，示例代码是围绕着z轴旋转的，所以传入的是(0, 0, 1);
xformMatrix.setRotate(ANGLE, 0, 0, 1);
......
// Matrix4对象的elements属性访问存储矩阵元素的类型化数据
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix.elements);
Matrix4对象支持的方法和属性
从上表中可见，Matrix4对象有两类方法
- 含有set前缀：根据参数计算出变换矩阵，将矩阵写入自身
- 不含有set前缀：根据参数计算出变换矩阵，将自身与刚刚计算得到的变换矩阵相乘，再把结果写回自身
示例代码中已有部分相应测试提供，可以根据提供的Matrix4对象的方法和属性，自行修改测试
复合变换
通过上一小节对Matrix4的使用有了基本的了解，并且第三章的最后综合练习通过手写变换矩阵，上一小节的示例代码也有了复合变换的示例，关于api的使用这里不再赘述
之前的例子中包含了两种变换
- 将三角形沿着x轴平移一段距离
- 在此基础上旋转一定的角度
书中提到了平移+旋转的矩阵等式组合过程
- 等式4.1 平移
- 等式4.2 在平移后进行旋转
- 等式4.3 将等式4.1与4.2组合
上一小节的Matrix4对象支持的方法和属性表，当中提到带有set前缀的方法是根据参数计算矩阵，写入自身，不带有set的则是根据参数计算矩阵，并与自身相乘再写回自身。
我们用代码来理解这个矩阵组合过程
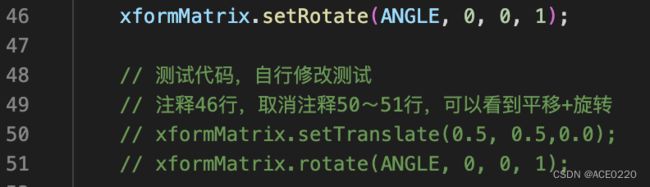
xformMatrix.setTranslate(0.5, 0.5, 0.0); // 方法带有set，根据参数计算矩阵，写回自身，等价于等式4.1
xformMatrix.rotate(ANGLE, 0, 0, 1); // 方法不带有set，根据参数计算矩阵，并与自身相乘，等价于等式4.2
将这些变换复合成一个等式的变换，就得到模型变换，或称为建模变换，相应的变换矩阵称为模型矩阵
接下来复习一下矩阵的乘法
要注意的是，矩阵乘法中的次序是很重要的，AB != BA。
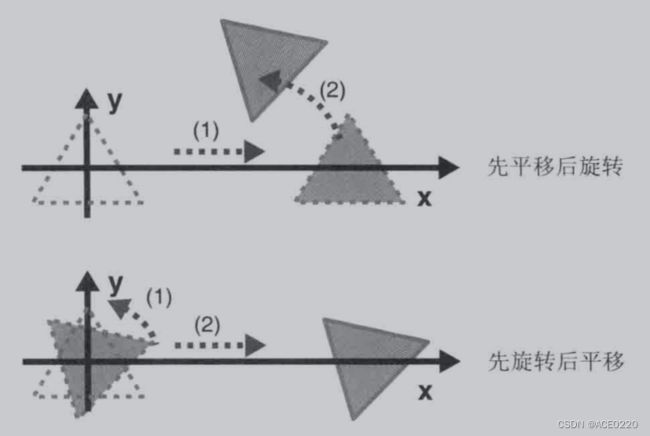
通过示例代码RotatedTranslatedTriangle.js，展示平移旋转 和 旋转平移的区别
示例和实验代码RotatedTranslatedTriangle.js
关键代码在31和32行，先通过setRotate()，传入的参数用以计算旋转矩阵，写入modelMatrix，再调用translate()，先计算出新的平移矩阵，用存储在modelMatrix中的矩阵乘以新的平移矩阵，再写入modelMatrix，经过这两步后，modelMatrix中存储的是<旋转矩阵>*<平移矩阵>
实验代码位于35～36行，可以尝试自行推导
<旋转矩阵>*<平移矩阵>的效果
<平移矩阵>*<旋转矩阵>的效果
平移和旋转次序不同，导致不同的结果，因为旋转是绕着原点进行旋转，当三角形位于原点和不位于原点，旋转的情况就会不同
动画
通过本章前面小节的练习，学到部分矩阵变换操作的知识的，下一步，将矩阵变换运用到动画图形中。
动画基础
为了让一个三角形不停的旋转，需要做的是：不断擦除和重绘三角形，每次重绘轻微的改变角度
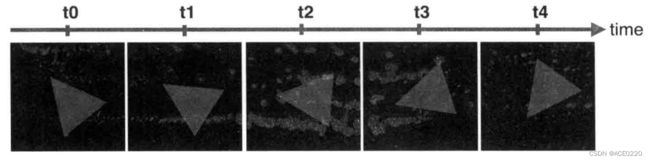
通过下图，我们可以看到，随着时间的推进，三角形每次的角度都略有不同，按照顺序快速的连续看到这些图，大脑会不自觉地对影像进行插值，从而形成流畅的动画。
每次重绘都要将上一个三角形擦除，绘制之前都要调用gl.clear().
生成动画需要两个关键机制：
- 在各个时刻反复调用同一个函数来绘制三角形
- 每次绘制之前都要擦除上次绘制的内容，并且调整三角形的角度
机制二我们在多次练习中已经实现很多次了
gl.clearColor()
gl.clear
gl.drawArrays()
如何实现机制一，是一个新的问题，我们通过一个示例代码RotatingTriangle.js来研究机制一
先放出示例代码的效果
示例代码：RotatingTriangles.js
对于示例代码的重点部分做了注释，打开代码查看
反复调用绘制函数tick
前面所述，为了使三角形旋转，需要两步
- 更新三角形当前角度currentTriangle，通过animate函数
- 调用绘制函数，根据当前角度绘制三角形，通过tick函数
我们将这两个步骤写在匿名函数中，然后赋值给tick变量，关于匿名函数的部分复习一下第二章46页开始，或者自行查找js相关书籍
draw函数按照指定旋转角度绘制三角形
draw()被设计为接收一下五个参数
- gl : 上下文
- n : 顶点个数
- currentAngle : 当前旋转角度
- modelMatrix : 根据currentAngle计算出的旋转矩阵，存储在Matrix4对象中
- u_ModelMatrix : 顶点着色器同名的uniform变量
函数的设计部分，只不过是把之前的绘制流程抽出来作为一个单独的函数，理论上不影响理解，参考代码进行理解
requestAnimationFrame()函数
传统习惯上，js重复执行某个特定任务可以使用setInterval()函数，后来浏览器引入了requestAnimationFrame()方法，该方法只会在当前标签页被激活状态才会生效。google提供的webgl-utils.js库隐藏了该函数的定义和浏览器间的差异
使用这个函数的好处是可以避免在未激活的标签上运行动画，减轻浏览器的负担，坏处是无法指定重复调用的间隔。
浏览器也不会因为我们发起一次请求就会无限循环调用func
有请求则有取消，我们可以通过cancelAnimationFrame(requestID)取消请求
函数规范
更新旋转角animate()
上面我们简单了解了requestAnimationFrame()函数的机制，由于每个时刻调用tick()函数的间隔是不同的，只是通过请求浏览器在适当时间调用函数，浏览器会根据自身状态决定什么时候调用。
所以animate函数中，newAngle的角度是根据上一次调用和这次调用的时间间隔去计算角度值，并且保证旋转角度在0～360之间。
实验程序
在RotatingTriangles.js的基础上已附上实验代码。
另外附上一个实验代码，通过按钮动态的控制旋转速度
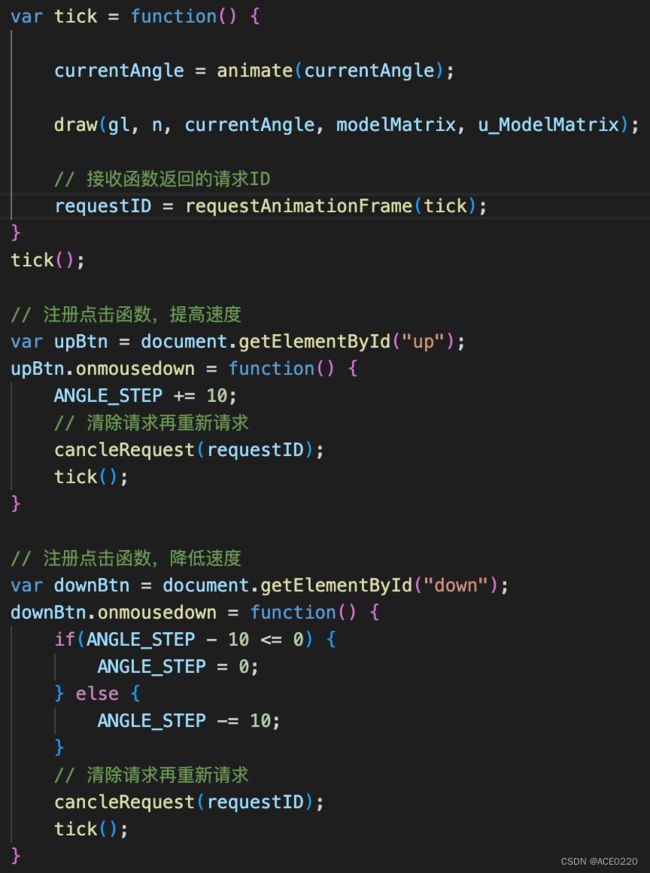
示例代码：RotatingTriangle_withButtons.js
主要修改的部分如下图所示，这里不再赘述
总结
本章中主要研究了使用矩阵库对图形进行变换，组合复杂变换，将变换应用于动画中等。
要了解两个关键点
- 复杂变换可以通过基本变换矩阵相乘的到
- 反复变换和重绘可以生成动画效果