实体对齐(三):RNM
一.摘要
实体对齐旨在将来自不同知识图(KG)的具有相同含义的实体联系起来,这是知识融合的重要步骤。 现有研究侧重于通过利用知识图谱的结构信息学习实体嵌入来进行实体对齐。这些方法可以聚合来自相邻节点的信息,但也可能带来来自邻居的噪声。 最近,一些研究人员试图成对比较相邻节点以增强实体对齐。然而,他们忽略了实体之间的关系,而实体之间的关系对于邻域匹配也很重要。 此外,现有方法较少关注实体对齐和关系对齐之间的正交互作用。为了解决这些问题,我们提出了一种名为 RNM 的新型关系感知邻域匹配模型,用于实体对齐。 具体来说,我们建议利用邻域匹配来增强实体对齐。 除了在匹配邻域时比较邻居节点外,我们还尝试从连接关系中探索有用的信息。 此外,迭代框架旨在以半监督的方式利用实体对齐和关系对齐之间的正交互作用。 三个真实世界数据集的实验结果表明,所提出的模型 RNM 比最先进的方法表现更好。
二.背景介绍
在知识图谱 (KG) 中,事实表示为 (h, r, t) 的三元组,表示从头部实体 h 到尾部实体 t 存在关系 r。 真实世界的知识图谱,如 DBpedia、YAGO 和 Freebase,存储了大量知识,已被用于推荐系统、问答和搜索引擎等各种应用程序。
但是,每个单独的 KG 可能是不完整的。 由于不同的 KG 是从不同的数据源独立构建的,因此它们通常是相互补充的。 因此,整合来自不同 KG 的异构知识已成为一个紧迫的问题。 实体对齐是来自不同 KG 的知识融合的重要步骤,其目的是将来自不同 KG 的具有相同含义的实体联系起来。 因此,可以根据对齐的实体融合事实。
关于实体对齐任务,大多数现有研究都集中在构建基于嵌入的模型上。 这些方法试图将 KGs 的实体嵌入到潜在空间中,并计算实体向量之间的距离作为对齐的证据。 TransE作为一种有效的 KG 嵌入模型,已被广泛用于实体对齐 。 为了更好地利用来自邻居的信息,图卷积网络 (GCN)被用来改进实体的表示学习。 然而,这些方法专注于学习实体的综合嵌入,同时可能会带来来自邻居的额外噪音。
最近,一些研究试图在比较候选实体对时进行子图匹配以增强对齐。 然而,这些方法只比较了相邻实体而忽略了连接关系,而连接关系也包含了邻域匹配和实体对齐的重要信息。 此外,现有方法较少关注实体对齐任务和关系对齐任务之间的正向交互。我们的见解描述如下:首先,邻域与关系的匹配可以增强实体对齐的可靠性。 图 1 显示了实体对齐与邻域匹配的示例。 假设两个 KG 中的实体罗马、文艺复兴、佛罗伦萨和米开朗基罗已经对齐。 如果我们在匹配子图时只考虑相邻实体,KG1 中的实体 Italy (in Chinese) 更可能与 KG2 中的实体 David Statue 错位。 但是,如果我们同时比较连接关系并考虑关系资本的 1 对 1 属性,则实体 Italy 可以正确对齐跨越两个 KG。 这意味着关系在邻域匹配中不仅在语义上而且在映射属性上都起着重要作用。 其次,关系对齐可以帮助找到实体的对齐,另一方面,实体对齐也可以辅助关系对齐任务。具体来说,实体对齐可以根据相邻实体和链接关系推断,而关系对齐可以根据连接的头尾实体推断。 因此,在统一框架中实现实体对齐和关系对齐是合理的。
因此,在本文中,我们提出了一种名为 RNM 的新型关系感知邻域匹配模型,用于实体对齐。 除了在匹配子图时比较相邻实体外,我们还利用链接关系中的语义信息和映射属性进行实体对齐。 关系的语义信息帮助我们进行邻域关系匹配,而关系的映射属性提供了对齐的概率。 此外,我们设计了一个迭代框架来统一实体对齐和关系对齐,其中这两个任务可以以半监督的方式相互加强。 三个真实世界数据集的实验结果表明,RNM 明显优于几种最先进的方法。
三.RNM
图 2 说明了所提出的模型 RNM 的总体架构。 首先,给定两个 KG 和一组实体种子对齐集,我们使用 GCN 和类似 TransE 的正则化器共同学习实体和关系的嵌入。 之后,我们以半监督的方式迭代地对齐实体和关系。 在每次迭代中,我们利用图结构信息通过关系感知邻域匹配模块和实体感知实体匹配模块来分别确定新的实体和关系匹配对。

3.1 实体和关系的嵌入学习
为了对齐两个 KG 的实体,我们将它们嵌入到相同的潜在空间中以使其具有可比性。 类似地,我们将两个 KG 的关系嵌入到相同的潜在空间中以进行关系对齐。 为了探索知识图谱中实体和关系之间的相互作用,我们建议共同学习实体和关系的嵌入。
3.1.1 实体嵌入
给定两个 KG 和一组实体的种子对齐,我们利用 GCN 将两个 KG 的所有实体嵌入到同一个潜在空间中,同时考虑两个 KG 的结构信息。 我们使用预训练的词嵌入来初始化实体表示,这可以提供有用的实体语义信息。 此外,我们采用高速公路策略来控制多层 GCN 传播过程中的噪声。
我们将上述 GCN 的输出作为实体的嵌入,并将所有实体的最终表示定义为 X ~ = x ~ 1 , x ~ 2 , ⋅ ⋅ ⋅ x ~ n ∣ x ~ i ∈ R d ~ \widetilde X = {\widetilde x_1,\widetilde x_2, · · ·\widetilde x_n|\widetilde x_i ∈ R^{\widetilde d}} X =x 1,x 2,⋅⋅⋅x n∣x i∈Rd , 其中 d 表示实体嵌入的维度,n 表示实体的数量。 对于 e i ∈ E 1 e_i ∈ E_1 ei∈E1 和 e j ′ ∈ E 2 e'_j ∈ E_2 ej′∈E2 的实体对 (ei, e’j),我们将它们之间的距离定义为:

较小的 d ( e i , e j ′ ) d(e_i, e'_j) d(ei,ej′) 表示两个实体 $e_i $和 $e’_j $之间对齐的概率较高。
为了将两个知识图谱的实体嵌入到同一个潜在空间中,我们将种子对齐作为训练数据,并为实体对齐设计了一个基于边缘的损失函数,如下所示:

其中 L 表示预对齐实体对的集合,L’ 是最近邻采样时的一组负对齐,γ > 0 表示边距。 损失函数假设对齐的实体对之间的距离应该接近于零,而负样本之间的距离应该尽可能远。
3.1.2 关系嵌入
在 KG 中,事实被编码为三元组,即 (h, r, t),其中 h 表示头实体,t 表示尾实体,r 表示从 h 到 t 的关系。因此,关系的含义 与其两个连接的实体相关联。 为了利用连接实体的信息,我们利用从 GCN 中学习到的头部实体和尾部实体的嵌入来表示知识图谱中的关系,可以写成如下形式:

其中 r ∈ R 2 d ~ r∈R^{2 \widetilde d} r∈R2d 表示关系 r ∈ R 1 ∪ R 2 r ∈ R_1 ∪ R_2 r∈R1∪R2 的嵌入,concat 表示串联操作, g r h g^h_r grh 和 g r t g^t_r grt 分别表示 r 的所有不同头实体和尾实体的平均嵌入。
此外,为了进一步探索基于三元组的关系的翻译信息,受 TransE 的启发,我们设计了一个正则化器,如下所示,

其中 T 1 T_1 T1 和 T 2 T_2 T2 分别表示两个给定 KG G 1 G_1 G1 和 G 2 G_2 G2 的三元组集。 W R ∈ R d ~ × 2 d ~ W_R∈R^{\widetilde d×2\widetilde d} WR∈Rd ×2d 表示从潜在关系空间到潜在实体空间的变换矩阵,这是要学习的模型参数。
3.1.3 目标函数
其中 λ 是一个权衡系数,用于平衡实体对齐的损失和考虑到关系嵌入的正则化损失。 我们的目标是在实体嵌入的预训练之后最小化上面的函数。 此外,我们利用 Adam进行目标优化。
3.2 关系感知邻域匹配
GCN 旨在聚合来自相邻节点的信息,但也可能带来来自邻居的一些额外噪声。 为了减少这些噪声的影响,我们提出了一种关系感知邻域匹配模型来比较实体对。 我们假设如果来自不同知识图谱的两个实体已经对齐,那么具有相同意义的关系,可以根据关系的映射属性推断出两个指向尾部实体的对齐概率。例如,1-to-1 关系可以提供精确对齐,而 1-to-N 关系只能显示 1/N 的概率。
对于每个候选实体对 ( e i , e j ′ ) (e_i, e'_j) (ei,ej′) ,其中 e i ∈ G 1 e_i ∈ G_1 ei∈G1 和 e j ′ ∈ G 2 e'_j ∈ G_2 ej′∈G2,除了成对比较它们的单跳邻居实体外,我们还考虑连接关系之间的比较。 具体地,设 N e i N_{e_i} Nei 为 e i e_i ei在 G 1 G_1 G1中的一步邻居实体集合, N e j N_{e_j} Nej为 e j ′ e'_j ej′在 G 2 G_2 G2中的一步邻居实体集合。对于关于 e i e_i ei 和 e j ′ e'_j ej′ 的邻域匹配,我们比较 C i j e = ( n 1 , n 2 ) , ( r 1 , r 2 ) ∣ n 1 ∈ N e i , n 2 ∈ N e j ′ , ( e i , r 1 , ( e i , r 1 , n 1 ) ∈ T 1 , ( e j ′ , r 2 , n 2 ) ∈ T 2 C^e_{ij} = {(n_1, n_2),(r_1, r_2)|n_1 ∈Ne_i, n_2 ∈ Ne'_j,(e_i, r_1,(e_i, r_1, n_1) ∈ T_1,(e'_j, r_2, n_2) ∈ T_2} Cije=(n1,n2),(r1,r2)∣n1∈Nei,n2∈Nej′,(ei,r1,(ei,r1,n1)∈T1,(ej′,r2,n2)∈T2 ,其中 T 1 T_1 T1 和 T 2 T_2 T2 分别是两个知识图谱的三元组集合。之后,我们关注具有匹配关系的匹配邻居,这对于实体对齐至关重要。 因此,匹配集 M i j e M^e_{ij} Mije 定义为 C i j e C^e_{ij} Cije 的子集,其中元素满足 ( n 1 , n 2 ) ∈ L e (n_1, n_2) ∈ L_e (n1,n2)∈Le 和 ( r 1 , r 2 ) ∈ L r (r_1, r_2) ∈ L_r (r1,r2)∈Lr,其中 L e L_e Le 表示实体的对齐集, L r L_r Lr 表示对齐集 的关系。
此外,连接关系的映射属性对于实体对齐也很重要。 因此,对于 M i j e M^e_{ij} Mije 中的每个匹配案例,我们将计算基于 r1, r2 和 n1, n2 的对齐概率,可以写成如下形式:

P(r1, n1) 和 P(r2, n2) 分别表示对应关系和邻居实体的映射概率。 因此,我们可以如下更新两个实体之间的距离:

其中 λ e λ_e λe 是控制嵌入距离和匹配分数之间权衡的超参数。匹配分数越大表示候选实体对对齐的概率越高。
3.3 实体感知关系匹配
对于来自不同知识图谱的两个关系,我们假设头实体和尾实体在其关联的三元组中同时对齐的次数越多,这两个关系越有可能具有相同的含义。 对于关系 r,我们将 S r = ( h , t ) ∣ ( h , r , t ) ∈ T S_r = {(h, t)|(h, r, t) ∈ T} Sr=(h,t)∣(h,r,t)∈T 定义为其相关实体对的集合,其中 T 表示给定 KG 中的三元组集合。因此,给定候选关系对 ( r i , r j ′ ) (r_i, r'_j) (ri,rj′),其中 r i r_i ri 来自 G1, r j ′ r'_j rj′ 来自 G2,我们首先形成相应的实体对集 S r i S_{r_i} Sri 和 S r ′ j S_{{r'}_j} Sr′j。 然后,我们比较 C i j r = ( h 1 , h 2 ) , ( t 1 , t 2 ) ∣ ( h 1 , t 1 ) ∈ S r i , ( h 2 , t 2 ) ∈ S r j ′ C^r_{ij} = {(h_1, h_2),(t_1, t_2)|(h_1, t_1) ∈ S_{r_i},(h_2, t_2) ∈S_{r'_j}} Cijr=(h1,h2),(t1,t2)∣(h1,t1)∈Sri,(h2,t2)∈Srj′ 中的所有实体对,并将匹配集 M i j r M^r_{ij} Mijr 定义为 C i j r C^r_{ij} Cijr的子集,其中元素满足 ( h 1 , h 2 ) ∈ L e (h_1, h_2) ∈ L_e (h1,h2)∈Le 和 ( t 1 , t 2 ) ∈ L e (t_1, t_2) ∈ L_e (t1,t2)∈Le 的条件。 因此,关系对 ( r i , r j ′ ) (r_i, r'_j) (ri,rj′) 之间的距离可以更新如下:

其中 λ r λ_r λr 是权衡系数。 与实体对的距离度量类似,我们同时考虑了关系对的嵌入距离和匹配分数。
3.4 迭代策略和实施细节
为了利用实体对齐任务和关系对齐任务之间的正向交互,我们设计了一个半监督框架,其中实体对齐和关系对齐可以迭代地相互增强。令 D e ∈ R ∣ E 1 ∣ × ∣ E 2 ∣ D^e ∈ R^{|E_1|×|E_2|} De∈R∣E1∣×∣E2∣ 表示实体对从 KG1 到 KG2 的距离矩阵, D r ∈ R ∣ R 1 ∣ × ∣ R 2 ∣ D^r ∈ R^{|R_1|×|R_2|} Dr∈R∣R1∣×∣R2∣ 表示从 KG1 到 KG2 的关系对的距离矩阵。 算法 1 给出了 RNM 的迭代策略:

D e D^e De 的初始化定义如下,其中包含学习到的实体嵌入:

D r D^r Dr 的初始化可以用学习到的关系嵌入写成如下:
![]()
D e D^e De 和 D r D^r Dr 可用于对齐排序或对齐集生成。 生成或更新对齐集的方法如算法 2 所示:

此外,我们引入反向关系来丰富知识图谱。 例如,对于事实 (Tokyo, CapitalOf, Japan),我们还将构建另一个三元组 ( J a p a n , C a p i t a l O f − 1 , T o k y o ) (Japan, CapitalOf^{-1} , Tokyo) (Japan,CapitalOf−1,Tokyo)。 因此,给定 KG 的关系集和三元组集将相应地扩大。
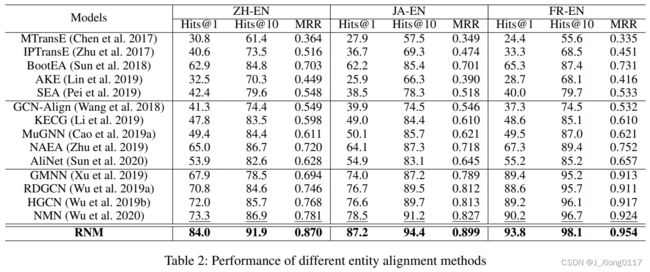
3.5 实验结果
四.总结
本文提出了一种名为RNM的新型关系感知邻域匹配模型,用于实体对齐。 模型共同学习实体和关系的嵌入。 此外,利用关系的语义信息和映射属性来实现更好的实体对齐并且以半监督相互加强的方式迭代地实现实体对齐和关系对齐。在三个跨语言KG数据集上评估了模型,结果证明了RNM的有效性。
五.附录
论文链接:https://arxiv.org/pdf/2012.08128.pdf
代码链接:https://github.com/Peter7Yao/RNM