深度学习笔记（MNIST手写识别）

先看了点花书，后来觉得有点枯燥去看了b站up主六二大人的pytorch深度学习实践的课，对深度学习的理解更深刻一点，顺便做点笔记，记录一些我认为重要的东西，便于以后查阅。

一、 机器学习基础

学习的定义：

对于某类任务T核性能度量P，一个程序被认为可以从经验E中学习是指，通过E改进后，在任务T上由P衡量的性能有所提升。

常见学习任务

一、分类
二、输入缺失分类
三、回归
四、转录

无监督学习和监督学习

1）无监督学习设计观察随机向量x的好几个样本，试图显示或隐式地学习出概率分布p(x),在无监督学习中，算法必须在没有指导的情况下理解数据。

2）监督学习包含观察随机向量x及其相关联的值或向量y，然后从x预测y，即存在“老师”，提供目标y给机器学习系统，指导其应该做什么。

传统上回归、分类、结构化输出问题称为监督学习

线性回归

线性回归解决回归问题，我们的目标是建立一个系统，将向量 $x\in R^n$作为输入，预测标量$y\in R$ 作为输出。$\hat{y}$表示模型预测y应该取得值，定义
$$\hat{y}={\omega }^{\top }x$$
$\omega \in R^n$是参数向量
$\omega$是一组权重，决定每个特征如何影响预测的权重。

测试集

我们有m个输入样本组成的设计矩阵，不用它来训练模型，而是用来评估模型性能如何。同样有每个样本对应的正确值y组成的回归目标向量。此为test set，将输入 的设计矩阵记作${\mathbf{X}}^{(test)}$,回归目标向量记作${\mathbf{y}}^{(test)}$。而度量模型性能的一种方法是计算模型在测试集上的均方误差(mean squared error) ，${\hat{\mathbf{y}}}^{(test)}$代表模型在测试集上的预测值，则MSE表示为
$$MS{E}_{test}=\frac{1}{m}\sum _i({\hat{\mathbf{y}}}^{(test)}-{\mathbf{y}}^{(test)}{)}_i^2$$当预测值和目标值之间的欧几里得距离增加时，误差也增加。
为构建算法，需设计一个算法通过观察${\mathbf{X}}^{(train)}$和${\mathbf{y}}^{(train)}$获得经验，减少$MS{E}_{test}$以改进权重$\omega$
线性回归会附加额外参数截距项b，此映射仍为线性函数。b通常被称为仿射变换的bias参数。
$$\hat{y}={\omega }^{\top }x+b$$

容量、过拟合、欠拟合

我们的算法必须在先前未观测到的新输入上表现良好，这种能力称为泛化(generalization)

梯度下降

用整个数据集效率低，使用随机梯度下降，效率高，但相应的时间复杂度高，因此采取折中使用batch，mini-batch，小批量的进行随机梯度下降。
$$w=w-\alpha \frac{\partial (cost)}{\partial w}$$

反向传播

首先关于激活函数的由来，因为$\hat{y}=W_2(W_{1}X+b_1)+b2$可化简为$\hat{y}=W_2{W}_{1}X+W_2{b}_1+b_2=WX+b$即使层数多，最后依然线性模型，并不能增加复杂程度，因此需要在每个结果后增加一个Nonlinear Function激活函数$\sigma$

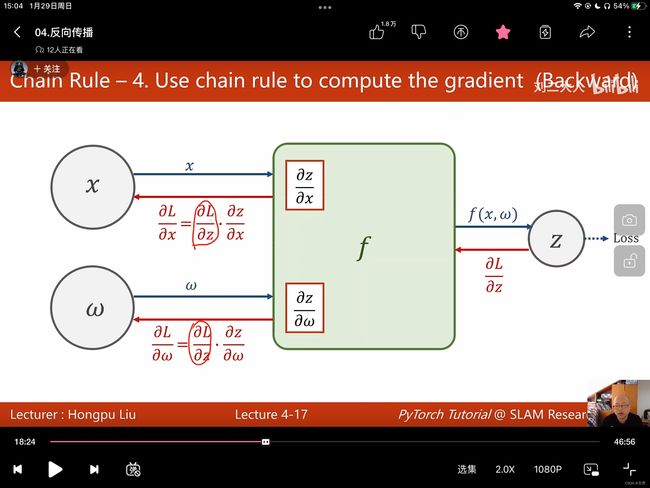
反向传播：我们要得到$\frac{\partial Loss}{\partial w}$，需要利用链式法则，下图清晰的描述了反向传播的过程。


在pytorch中，需要用到tensor，tensor保存了data和grad，代表了权重本身的值，以及损失对于此权重的梯度，即导数。

最后附此视频本章作业答案。b站刘二大人 第四讲

import torch
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w1 = torch.Tensor([1.0])
w1.requires_grad = True

w2 = torch.Tensor([1.0])
w2.requires_grad = True

b = torch.Tensor([1.0])
b.requires_grad = True

def forward(x):
    return w1 * x **2 + w2 * x + b

def loss(x, y):
    y_pred = forward(x)
    return (y_pred-y) ** 2

print("predict (before training)", 4, forward(4).item())  #item() 是为了取得标量

mse_list=[]
for epoch in range(1000):
    for x, y in zip(x_data, y_data):
        l = loss(x,y)
        l.backward()
        print('\tgrad:',x, y, w1.grad.item(),w2.grad.item(),b.grad.item())
        w1.data = w1.data - 0.01 * w1.grad.data   #更新权重时，不能使用张量， 而要使用data
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data
        w1.grad.data.zero_()    #将w的梯度清零
        w2.grad.data.zero_()
        b.grad.data.zero_()
    print("progress:",epoch, l.item())
    mse_list.append(l.item())
print("predict (after training)",4,forward(4).item())
plt.plot(range(1000), mse_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

第五讲 用Pytorch实现线性回归

线性回归就是只有一个神经元的神经网络

步骤
1、prepare dateset 准备数据集
2、design model using Class 设计模型（计算$\hat{y}$)
3、construct loss and optimizer 构建损失函数以及优化
4、training cycle 训练周期（前馈、反馈、更新）

一个$z=wx+b$代表一个Linear Unit即线性单元

代码：

import torch

x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])

class LinearModel(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = torch.nn. Linear(1, 1)

    def forward(self, x):
        y_pred = self.linear(x)
        return y_pred

model = LinearModel()  #模型

criterion = torch.nn.MSELoss(size_average= False) #求损失，传入yhat和y

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)    #优化器

for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    optimizer.zero_grad()    #梯度清零
    loss.backward()			 #反向传播
    optimizer.step()

print('w=', model.linear.weight.item())
print('b=', model.linear.bias.item())

x_test = torch.tensor([[4.0]])
y_test = model(x_test)

print('y_pred', y_test.data.item())

明显感觉，很多步骤pytorch都替我们弄好了，只需要调用函数即可，很方便。

第六讲 logistic regression （分类问题）

分类问题输出的是一个概率，对于数字0-9本身抽象类型不构成大小比较，满足分布。

tochvision 还提供了 CIFAR-10 dataset ，是一些图片比如车、飞机等

import torchvision
train_set = torchvision.datasets.MNIST(root='../dataset/mnist', train= True, download= True)
test_set = torchvision.datasets.MNIST(root='../dataset/mnist', train= False, download= True)

将mnist改为CIFA10即可

在分类中 输出的是$p(\hat{y})$即此结果的概率。

sigmoid 函数：满足0-1且饱和函数
最出名的就是logistic function：$\sigma (x)=\frac{1}{1+e^{-x}}$

线性单元：$\hat{y}={\omega }^{\top }x+b$
logistic function 单元就是用sigma去作用即：$\hat{y}=\sigma ({\omega }^{\top }x+b)$

同样的损失函数也不再是一个差，而是一个分布
$$loss=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$$binary cross entropy
BCE损失函数，
KL散度、交叉熵（一堆概率论的知识点、还没学）

同样是四步

第七讲 处理多维特征的输入

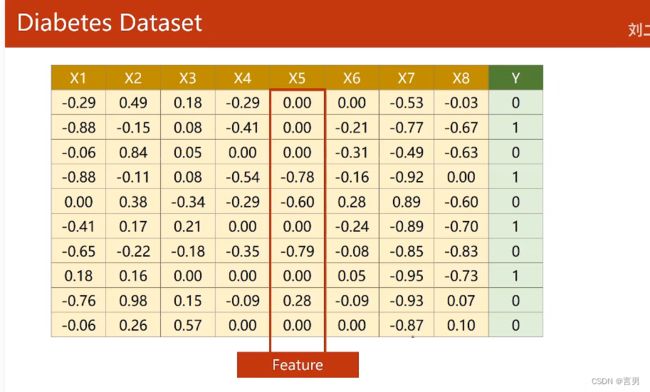
这样的一些样本，每一行是一个record，每一列每个x是一个feature即特征。

没想到anaconda下还有数据库啊

D:\anaconda3\Lib\site-packages\sklearn\datasets\data

对于多维的，比如上面的一行一个记录
需要的模型则变成
$${\hat{y}}^{(i)}=\sigma (\sum _{n=1}^8{x}_n^i\cdot {\omega }_n+b)=\sigma (z_i)$$

当有N个样本时，参数w则可写为N×8的矩阵，b也需要写成8×1的矩阵。

代码只需将Linear(1,1) 改为Linear(8,1),即输入为8维，一个样本的纬度值，输出为1维

class Model(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = torch.nn.Linear(8,1)
        self.sigmoid = torch.nn.Sigmoid()
        
    def forward(self, x):
        x = self.sigmoid(self.linear(x))
        return x

model = Model()

将多个unit首位相连即可构造神经网络，本质就是进行矩阵的乘法运算。找到一个n维到1维的非线性空间变化，利用多层的运算来模拟非线性。

课中的例子用的的diabetes的数据集进行3个神经元的训练，整体的代码如下

import torch
import numpy as np
import matplotlib.pyplot as plt
xy = np.loadtxt('diabetes.csv.gz',delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1])  #取出除了最后一列的数据
y_data = torch.from_numpy(xy[:, [-1]]) #只拿最后一列，且以矩阵的形式

class Model(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x)) #一般最后一个使用sigmoid 其他可relu
        return x

model = Model()
criterion = torch.nn.BCELoss(size_average = False)  #交叉熵
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(100): #训练基本不变
    #forward
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    #backward
    optimizer.zero_grad()
    loss.backward()

    #Update
    optimizer.step()

将epoch和loss作为x、y绘图后得，这里循环了5000次

第八讲 加载数据集

在梯度下降时，一种称为batch，需要用到全部的样本，另一种称为随机梯度下降，只用一个样本，随机性较好，可克服鞍点问题，batch的优点是利用向量计算的优势，提高计算的速度。
综合考虑，使用mini-batch

概念：Epoch、Batch-size、Iteations

#Training cycle
for epoch in range(training_epochs): //外层是训练周期
	#loop over all batches
	for i in range(total_batch):  //内层是batch的迭代

Epoch：所有的样本都参与了一次前馈传播和反馈传播
Batch-size：一次前馈和反馈的训练样本的数量
Iteration：内层的迭代次数 number of pass
举例，epoch10000次， batch-size大小为1000， 则iteration为10

DataLoader：batch_size=2 shuffle=True

将Dataset打乱后进行分组打包成batch

第九讲 多分类问题

最后一层归一化 softmax layer，目的是为了满足概率分布
softmax function：
$$P(y=i)=\frac{e^{z_i}}{{\sum }_{j=0}^{K-1}{e}^{z_j}}$$
其中$z_i$是最后一层的输出，此时保证了结果输出和为1.保证了概率分布的条件

对于损失函数loss：$-Ylog\hat{Y}$

import torch
y = torch.LongTensor([0])
z = torch.Tensor([[0.2, 0.1, -0.1]])
criterion = torch.nn.CossEntropyLoss()  #从softmax到求对数输出合起来写了个交叉熵函数
loss = criterion(z,y)
print(loss)

处理MNIST
图片以Pillow的格式存储，我们首先利用transform将PIL 图像转为Image
$${\mathbb{Z}}^{28\times 28},pixel\in \{0,...,255\}$$变成$${\mathbb{R}}^{1\times 28\times 28},pixel\in [0,1]$$
其中1为通道，本数据集为单通道图片，彩色RGB则为3通道。28x28是图片高和宽

构建模型时，输入的是一个(N,1,28,28）的四阶张量，但因为神经网络中输入样本为矩阵，每个样本占一行，则首先将其变为1阶向量。即变成(N,784) x=x.view(-1,784)此处填-1可以自动算出N的值。

实现MNIST手写识别完整代码如下

import torch
from torchvision import datasets
from torchvision import transforms
import torch.optim as optim
batch_size = 64
from torch.utils.data import DataLoader

transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307, ), (0.3081, ))])
#nomalize均一化，后面两个参数是均值和标准差，此处是前人已算好的
#处理图像张量，将数值压在0-1之间
#利用ToTensor将PIL Image 变成 Tensor

train_dataset = datasets.MNIST(root='../dataset/mnist', train=True, transform=transform, download=True) #训练集
test_dataset = datasets.MNIST(root='../dataset/mnist', train=False, transform=transform, download=True) #测试集

train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)

class Net(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.l1 = torch.nn.Linear(784, 512)  
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)
        self.Relu = torch.nn.ReLU()   #激活函数采用relu
    def forward(self,x):
        x = x.view(-1, 784)
        x = self.Relu(self.l1(x))
        x = self.Relu(self.l2(x))
        x = self.Relu(self.l3(x))
        x = self.Relu(self.l4(x))
        return self.l5(x)  #最后一层输出不需要激活

model = Net()

criterion = torch.nn.CrossEntropyLoss()  #交叉熵损失
optimizer = optim.SGD(model.parameters(),lr=0.01, momentum=0.5)

def train(epoch):  # 封装训练函数
    running_loss = 0.0   # 累计的loss
    for batch_idx, data in enumerate(train_loader,0):
        inputs, target = data
        optimizer.zero_grad()   #清零

        #forward+backward+update
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx %300 ==299:    
            print('[%d, %5d] loss: %3f' % (epoch + 1, batch_idx + 1, running_loss/300))
            running_loss = 0.0


def test():   #封装测试函数
    correct = 0
    total = 0
    with torch.no_grad():  #不再计算梯度
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)
            total +=labels.size(0)
            correct += (predicted == labels).sum().item()
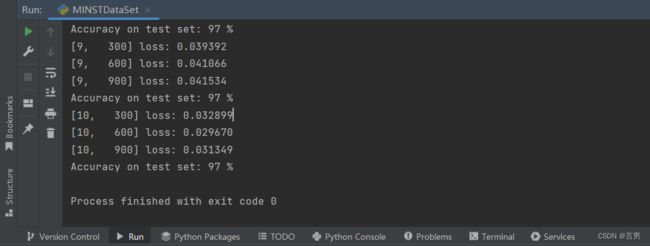
    print('Accuracy on test set: %d %%' % (100*correct / total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

最后结果如下：

剩下四讲为卷积神经网络和循环神经网络准备重开一篇。