何为非侵入式负荷分解-深度学习算法实现

1 前言

        做负荷分解的网络很多，本篇用contrib中的几个网络对AMPds数据集进行训练和测试。本篇内容较短。仅展示部分网络的代码和结果。        

2 数据集

        AMPds数据集所选电器见下表。电器选择原则如下：

        1）所选电器种类丰富，包括二态电器（如电视、冰箱）、多态电器（如洗衣机、洗碗机），这些电器具有代表性。

        2）数据集中其他分支，如卧室，厨房，电子工作台等不具有代表性。

        3）所选电器的功耗占据了家庭住户中绝大部分的电力功耗。

        电器描述

电器	描述
TVE	电视
HPE	热泵
FRE	强制空气炉:风扇和恒温器
FGE	冰箱
DWE	洗碗机
CWE	洗衣机
CDE	干衣机

2 深度学习网络代码

seq2seq

def seq2seq(window_length):

    model = Sequential()
    # 1D Conv
    model.add(Conv1D(30,10,activation="relu",input_shape=(window_length,1),strides=2))
    model.add(Conv1D(30, 8, activation='relu', strides=2))
    model.add(Conv1D(40, 6, activation='relu', strides=1))
    model.add(Conv1D(50, 5, activation='relu', strides=1))
    model.add(Dropout(.2))
    model.add(Conv1D(50, 5, activation='relu', strides=1))
    model.add(Dropout(.2))
    model.add(Flatten())
    model.add(Dense(1024, activation='relu'))
    model.add(Dropout(.2))
    model.add(Dense(window_length))
    model.compile(loss='mse', optimizer='adam')
    return model

seq2point

def seq2point(window_length):
    # Model architecture
    model = Sequential()
    model.add(Conv1D(30,10,activation="relu",input_shape=(window_length,1),strides=1))
    model.add(Conv1D(30, 8, activation='relu', strides=1))
    model.add(Conv1D(40, 6, activation='relu', strides=1))
    model.add(Conv1D(50, 5, activation='relu', strides=1))
    model.add(Dropout(.2))
    model.add(Conv1D(50, 5, activation='relu', strides=1))
    model.add(Dropout(.2))
    model.add(Flatten())
    model.add(Dense(1024, activation='relu'))
    model.add(Dropout(.2))
    model.add(Dense(1))
    model.compile(loss='mse', optimizer='adam')  # ,metrics=[self.mse])
    return model

dae

def dae(window_length):
    model = Sequential()
    model.add(Conv1D(8, 4, activation="linear", input_shape=(window_length, 1), padding="same", strides=1))
    model.add(Flatten())
    model.add(Dense((window_length)*8, activation='relu'))
    model.add(Dense(128, activation='relu'))
    model.add(Dense((window_length)*8, activation='relu'))
    model.add(Reshape(((window_length), 8)))
    model.add(Conv1D(1, 4, activation="linear", padding="same", strides=1))
    model.compile(loss='mse', optimizer='adam')
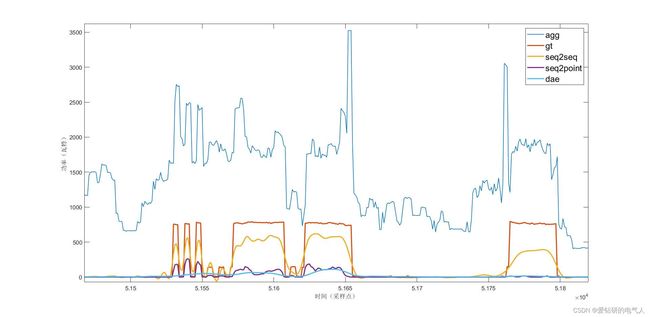
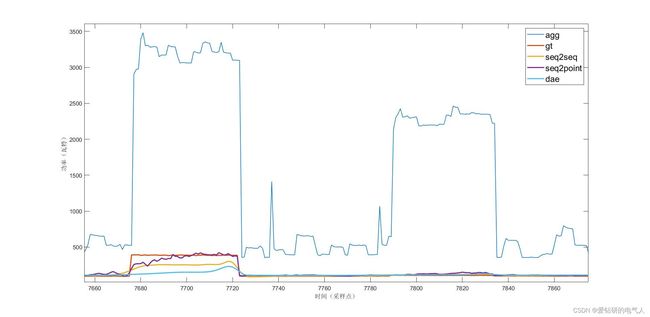
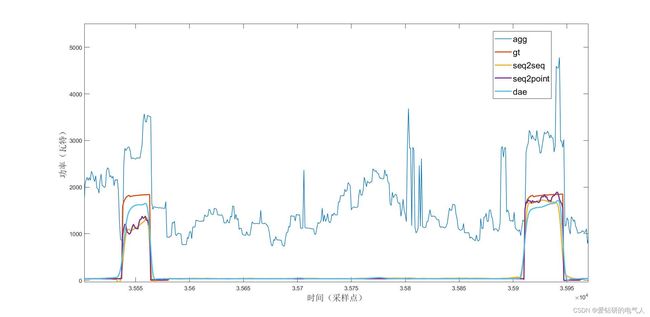
    return model

3 结果展示

        所有模型的窗口大小统一为256，256为随意选的。

CDE

DWE

FRE

HPE

TVE

        从分解结果可以看出seq2seq的效果更稳定。

 4 指标

		H=30
		TVE	HPE	FRE	FGE	DWE	CWE	CDE
seq2seq	mse	47.8891	182.0226	32.45976	59.5152	62.92132	24.73551	142.3779
	mae	19.41477	46.17111	17.49056	47.74608	11.3222	3.617367	14.72881
	sae	0.481338	0.216768	0.142687	1.038178	0.653079	1.044527	0.247477
	precision	0.894967	0.98622	1	0.949957	0.959572	0.424007	0.99147
	F_score	0.944573	0.993062	1	0.974337	0.979369	0.595512	0.995717
seq2point	mse	52.06977	163.0041	30.31967	64.2758	112.2182	27.99394	281.472
	mae	20.17212	37.0105	17.2002	51.04973	21.78895	4.655024	34.85449
	sae	0.500496	0.173588	0.140317	1.109909	1.255291	1.342523	0.584923
	precision	0.737554	0.982168	1	0.906464	0.349086	0.022703	0.928833
	F_score	0.848957	0.991004	1	0.950938	0.517515	0.044399	0.963103
DAE	mse	54.01654	198.6533	35.22556	67.77168	108.0763	27.73127	453.771
	mae	24.21881	56.29839	18.24221	61.01698	21.56635	5.229512	49.99487
	sae	0.600441	0.264314	0.148819	1.326737	1.243975	1.510039	0.840026
	precision	0.884315	0.998953	1	1	0.338748	0.063275	0.54253
	F_score	0.938606	0.999476	1	1	0.506067	0.119019	0.703429

		H=40
		TVE	HPE	FRE	FGE	DWE	CWE	CDE
seq2seq	mse	47.8891	182.0226	32.45976	59.5152	62.92132	24.73551	142.3779
	mae	19.41477	46.17111	17.49056	47.74608	11.3222	3.617367	14.72881
	sae	0.481338	0.216768	0.142687	1.038178	0.653079	1.044527	0.247477
	precision	0.817355	0.796572	1	0.865941	0.948671	0.325697	0.990495
	F_score	0.8995	0.886769	1	0.928155	0.973659	0.49136	0.995225
seq2point	mse	52.06977	163.0041	30.31967	64.2758	112.2182	27.99394	281.472
	mae	20.17212	37.0105	17.2002	51.04973	21.78895	4.655024	34.85449
	sae	0.500496	0.173588	0.140317	1.109909	1.255291	1.342523	0.584923
	precision	0.682134	0.681357	1	0.812462	0.309823	0.009509	0.917134
	F_score	0.811034	0.810485	1	0.896529	0.473076	0.01884	0.956776
DAE	mse	54.01654	198.6533	35.22556	67.77168	108.0763	27.73127	453.771
	mae	24.21881	56.29839	18.24221	61.01698	21.56635	5.229512	49.99487
	sae	0.600441	0.264314	0.148819	1.326737	1.243975	1.510039	0.840026
	precision	0.73546	0.692362	1	1	0.280281	0.034796	0.517183
	F_score	0.847568	0.81822	1	1	0.437843	0.067251	0.681767

        从指标上也可以看出seq2seq总体上效果最好。

 5 总结

        本篇的结果仅仅针对在Ampds下，窗口大小为256时，三种算法的对比。负荷分解就是不断在复现模型，修改模型的过程。效果好了，就能写论文了。欢迎大家讨论最新的网络，之后有时间也会更新对于一些新网络的复现。

6 建议

        很多入门的小白，在学习负荷分解时可以先根据一个模型把所有的流程都做一遍下来，熟悉了以后，接下来只需要对模型进行更换或者改进即可。一个完整的流程包括：数据处理、模型搭建、模型训练和测试、指标计算和结果可视化。当搭建了一个完整的流程后，以后看到别人的开源代码，你只需要提取其中的模型搭建部分的代码，然后放到自己的框架里面跑就行。这样你在对比各种算法时就更方便。毕竟没有人希望跑不同算法时，用不同的环境去跑，费时费力。