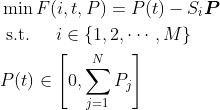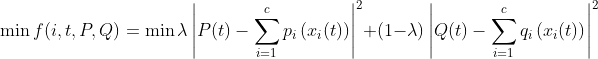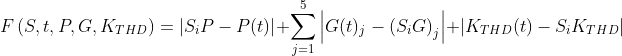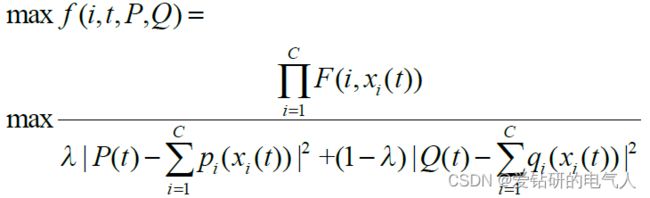何为非侵入式负荷监测之组合优化
1 前言
组合优化技术路线是不需要进行训练和测试，建立特征数据库后既可以直接对总负荷数据进行“分解”。组合优化的算法很多，所有能应用于整数规划的算法都是可以用的，常见的就是各种种群算法，以及他们的变体。也有听说要用神经网络做的，不过我还没见过，也没有研究，如果有这么干的同学，欢迎一起讨论。该技术路线核心在于2个部分：目标函数（适应度）和寻优算法。
2 目标函数
研究者们在目标函数这里下了不少功夫，目标函数的目的就是将总负荷的有功功率分解成已有电器运行的有功功率，其他的参数都是辅助算法得到更精确结果。
最常见的目标函数就是总负荷实时有功功率与电器组合后的有功功率差的绝对值[1]。
![P = \left [ P_{1},P_{2},P_{3},...,P_{n} \right ]](http://img.e-com-net.com/image/info8/29a472f6aff244279b50ecaadf1160fa.gif){kind=small}
其中，t是指总负荷的第t个点；
i是指第i个个体；
M是指中群中一共有M个个体；
P是特征数据库（特征向量）。
只用有功功率一个特征，算法的局限性大，因此有人提出使用有功和无功功率作为特征[2]。
是权重，通过可以调整对P和Q两种特征的占比。
也有研究者提出利用有功功率和谐波作为特征。
P(t)、G(t)、KD(t)分别为样本t时刻的总有功功率、谐波电流幅值、电流总谐波含量。
不同的特征组合下，就有不同的目标函数，这里不再赘述。
在确定了特征以后，仍要考虑的一点是寻优的效率。组合优化虽然不需要训练，但是测试时，每次只针对一个时刻的数据进行寻优，因此它的求解效率是比较低的。总负荷数据中，稳态的数据总是比暂态的数据多，也就是多，大部分相邻的点，他们组合优化的结果应该是一致，因此有人提出，从第二次寻优开始，将上一次寻优的结果作为初始化的值，这样可以有效的提高寻优的效率。也有研究者基于此，提出惩罚项，使用惩罚项的原理是鼓励寻优结果与前n次结果相同，如果发生变化则进行惩罚，这可以在一定程度上提高寻优的准确率[3]。
式中: F(i,xi(t))是状态概率因子,在认为各负荷的状态相互独立的情况下,F(i,x,(t))是t时刻点时各负荷的状态组合概率
总的来说，该技术路线在目标函数上的研究十分重要，有各种各样的改进都是为了提高寻优的效率或者效果。但是这类算法的硬伤就是他得保证总负荷就是由已知的电器组成的，而且由于特征数据库中的功率是固定值，所以运行波动大的电器会大大影响寻优的结果。同时这类方法针对的是总负荷的稳态数据，暂态是无法进行分解，因此需要事件检测辅助。
3 寻优算法
寻优算法太多了，我这里不一一列出，同时也不讲原理。常见的算法只需要百度就有相应的博客。
遗传算法——matlab实现_WFForstar的博客-CSDN博客_matlab遗传算法遗传算法https://blog.csdn.net/skyllerone/article/details/125080391
遗传算法-python版(计算机智能算法)_两只蜡笔的小新的博客-CSDN博客_python 遗传算法前言：遗传算法的原理及python实现一、原理二、整体步骤三、算法实例四、编程实现https://blog.csdn.net/weixin_44503976/article/details/120502554 粒子群算法(matlab实现)_jjb-coder的博客-CSDN博客_粒子群算法matlab目录基本原理算法概括式子说明程序设计基本流程代码部分总结基本原理算法概括粒子群算法(PSO),在PSO中,每个优化问题的潜在解都是搜索空间的一只鸟，被称为粒子，所有的粒子都有一个由适应度函数决定的适值，每个粒子还有一个速度决定它们“”飞行“”的方向和距离，然后粒子们就追随当前的最优粒子在解空间中搜索,整个过程大致为,PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代的过程中，粒子通过跟踪两个极值来更新自己:第一个就是粒子本身所找到的最优解,这个解称为个体极值;另一个极值是整个种https://blog.csdn.net/jiuzhongxian_/article/details/108286863
Python之粒子群算法（含代码实例）_偶做前堂客的博客-CSDN博客_粒子群算法pythonPython粒子群算法(含代码实例)https://blog.csdn.net/m0_60307882/article/details/123864693
print(pg)
print(pgfit)以粒子群为例，把个体的值和适应度打印出来，如下图所示。
4 总结
这个技术路线容易在寻优算法都很成熟了，改进的少，又或者改进的也容易写。寻优算法都是具有不确定性的，因此难在如何通过目标函数和新的判据让其稳定。另外，如何建立特征数据库也需要研究，现在常见的是通过聚类得到每类电器的特征值。
[1]崔灿. 面向智能用电的非侵入式居民负荷监测关键技术研究[D].华北电力大学(北京),2017.
[2]李如意,黄明山,周东国,等、基于粒子群算法搜索的非侵入式电力负荷分解方法[J].电力系统保护与控制, 2016, 44(08): 30-36.
[3]崔亮节. 基于多目标优化的非侵入式负荷分解方法研究[D].华北电力大学(北京),2020.DOI:10.27140/d.cnki.ghbbu.2020.000614.