2019_ICML_Domain Agnostic Learning with Disentangled Representations

论文地址：https://arxiv.org/pdf/1904.12347.pdf
代码地址：https://github.com/VisionLearningGroup/DAL

1 研究动机与研究思路

研究动机：之前的研究都有一个强假设，目标数据从同一分布均匀采样。本文提出Domain-Agnostic Learning (DAL)问题，即如何把有标注的源域信息迁移到无标注的任意目标域数据上。这个问题存在两个难点：1)目标数据来自混合的目标域，所以目前主流的特征对齐方法不太适用，2）类无关信息会导致负迁移，特别是当目标域高度异构的时候。
研究思路：一种深层对抗解耦自编码器( Deep Adversarial Disentangled Autoencoder，DADA )，能够将特定领域中分离出特定类的特征。

2 主要工作

本文的主要贡献在于：

• 提出了领域不可知学习的新范式；
• 提出了一个端到端的深层对抗解耦自动编码器( DADA )，更好的学习特征解耦表示；
• 提出用类解耦来去除类无关特征，并最小化互信息来增强解耦。

3 DADA

3.1 符号定义

定义领域无关学习任务如下：给定一个具有 $n_s$个标注样本的源域 ${\mathcal{D}}_s={\left\{\left({\mathbf{x}}_i^s,y_i^s\right)\right\}}_{i=1}^{n_s}$ ，目标是在没有域标注的情况下最小化$N$个目标域 ${\mathcal{D}}_t=\left\{{\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_N\right\}$ 上的风险。我们将有 $n_t$个未标注样本的目标域记为${\mathcal{D}}_t={\left\{{\mathrm{x}}_j^t\right\}}_{j=1}^{n_t}$。最小化目标风险${ϵ}_t(\theta )={\mathrm{Pr}}_{(\mathbf{x},y)\sim {\mathcal{D}}_t}[\theta (\mathrm{x})\ne y]$，其中$\theta (\mathrm{x})$为分类器。

3.2 DADA总框架

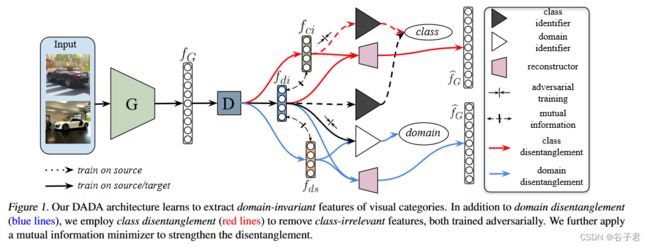
DADA方法学习提取视觉类别的领域不变特征。除了领域解耦(蓝线)，还使用类别解耦(红线)来去除类别无关的特征（在有标签的源域上训练一个类标识符，解耦器生成特征来欺骗类标识符），两者都是对抗训练的，进一步应用互信息最小化器来加强解耦。
图1展示了所提出的模型, 特征生成器 $G$ 将输入图片映射到特征向量 $f_G$, 这个 $f_G$ 是一个高度耦合的特征, 所以后面编码器 $D$ 的目的是将这个特征解耦为域不变特征 $f_{di}$, 域特定特征 $f_{ds}$ 和类无关特征 $f_{ci}$ 。特征重建器 $R$ 的目的是接受 $\left(f_{di},f_{ci}\right)$ 或 ( $f_{di},f_{ds}$ ) 作为输入, 然后重建出 $f_G$ 。 $D$ 和 $R$ 使用变分自编码器（VAE）中的编码器与解码器实现。为了增强解耦, 在 $\left(f_{di},f_{ci}\right)$ 以及 ( $f_{di}$, $f_{ds}$ ) 上进行互信息最小化约束。在域判别器支路（白三角) 通讨对抗训练学习出域不变特征 $f_{di}$ 。类判别器 $C$ (黒三 角) 通过在有标注的源域数据上预测类分布 $f_C$ 训练得到, 类无关特征 $f_{ci}$ 是通过结合 $C$ 以对抗的方式提取到的。

3.3 具体实现

3.3.1 变分自编码器

VAEs ( Kingma &韦林, 2013)是一类同时训练概率编码器和解码器的深度生成模型。编码器会生成符合高斯分布的隐藏向量。通过使用VAE来获得每个部分的解耦表示，损失函数设计如下：
L vae  = ∥ f ^ G − f G ∥ F 2 + K L ( q ( z ∣ f G ) ∥ p ( z ) ) \mathcal{L}_{\text {vae }}=\left\|\widehat{f}_G-f_G\right\|_F^2+K L\left(q\left(z \mid f_G\right) \| p(z)\right) Lvae ​= ​f ​G​−fG​ ​F2​+KL(q(z∣fG​)∥p(z))

这个式子前一项的目的是重建$G$提取的原始特征，后面一项计算Kullback - Leibler散度，惩罚隐藏特征分布与先验分布 $p\left(z_c\right)$(as $z\sim$ $\mathcal{N}(0,I)$ )的偏差。这个约束仅仅是将隐藏特征映射到一个标准分布（将潜在特征对齐到正态分布），并没有保证特征解耦。

3.3.2 类别解耦

通过对抗的方式实现类别信息解耦来移除一些类别无关的特征，比如背景等。首先通过源域数据进行有监督训练得到class identifier$C$（（图中黑色的三角））：
首先，在交叉熵损失的监督下，训练解耦器$D$和$K$ - way class identifier$C$来正确预测标签：

$${\mathcal{L}}_{ce}=-{\mathbb{E}}_{\left(x_s,y_s\right)\sim {\mathcal{D}}_s}\sum _{k=1}^{K}1\left[k=y_s\right]\log \left(C\left(f_D\right)\right)$$
其中 $f_D\in \left\{f_{di},f_{ci}\right\}$.固定住类判别器$C$来训练解耦器$D$来生成类无关特征$f_{ci}$来欺骗$C$。这可以通过最小化预测类分布的负交叉熵来实现：

$${\mathcal{L}}_{\text{ent }}=-\frac{1}{n_s}\sum _{j=1}^{n_s}\log C\left(f_{ci}^j\right)-\frac{1}{n_t}\sum _{j=1}^{n_t}\log C\left(f_{ci}^j\right)$$
第一项与第二项分别指的是在源域上和目标域上的交叉熵最小。上述对抗训练过程迫使相应的解缠器提取与类别无关的特征。

3.3.3 域解耦

为了实现源域与目标对齐，将学习到的特征分解为领域特定的和领域不变的特征，从而在领域不变的潜在空间中将源和目标领域对齐。这通过在得到的隐空间里进行对抗性域判别得到。具体来说，我们利用一个域标识符$DI$，它以解缠后的特征($(f_{di}$ or $f_{ds})$)作为输入，输出域标签$l_f$(源或目标)。领域标识符的目标函数为：
$${\mathcal{L}}_{DI}=-\mathbb{E}\left[l_f\log P\left(l_f\right)\right]+\mathbb{E}\left(1-l_f\right)\left[\log P\left(1-l_f\right)\right]$$
之后就训练解耦器$D$来欺骗域判别器$DI$来提取域不变特征。

3.3.4 互信息最小化

为了更好地分离特征，最小化领域不变和特定领域特征($\left(f_{di},f_{ds}\right)$)，以及领域不变和类别无关特征( $(f_{di}$, $f_{ci})$ )之间的互信息：
$$I\left({\mathcal{D}}_x;{\mathcal{D}}_{f_{di}}\right)={\int }_{\mathbb{X}\times \mathcal{Z}}\log \frac{d{\mathbb{P}}_{XZ}}{d{\mathbb{P}}_X\otimes {\mathbb{P}}_Z}d{\mathbb{P}}_{XZ},$$
其中， $x\in \left\{f_{ds},f_{ci}\right\},{\mathbb{P}}_{XZ}$的联合概率分布，$\left({\mathcal{D}}_x,{\mathcal{D}}_{f_{di}}\right)$, ${\mathbb{P}}_X={\int }_{\mathcal{Z}}d{\mathbb{P}}_{XZ}$ and ${\mathbb{P}}_Z=$ ${\int }_{\mathcal{X}}d{\mathbb{P}}_{XZ}$ 为边缘分布。尽管互信息是跨领域的关键度量，但它只适用于离散变量或有限的概率分布未知的问题。计算复杂度为$O\left(n^2\right)$，不适合深层的CNN。因此这篇文章采用的是互信息神经估计器(MINE):
$$I(X;Z{)}_n=\underset{\theta \in \Theta }{\sup }{\mathbb{E}}_{{\mathbb{P}}_{XZ}^{(n)}}\left[T_{\theta }\right]-\log \left({\mathbb{E}}_{{\mathbb{P}}_X^{(n)}\otimes {\mathbb{P}}_Z^{(n)}}\left[e^{T_{\theta }}\right]\right)$$
其中， $(x,z)$从联合分布中采样，$z^{\prime }$ 从边缘分布中采样。使用神经网络来执行方程7中定义的蒙特卡罗积分。

3.3.5 Ring-style Normalization

通过减去批均值除以批标准差来减少内部协变量偏移。尽管在领域自适应方面取得了很好的效果，但仅靠批量归一化并不足以保证嵌入的特征在异构领域场景中得到很好的归一化。目标数据从多个域中采样，其嵌入特征在隐空间中不规则分散。Zheng等人（2018）提出了ring-style norm constraint用于保证多类别的角分类边界（angular classification margins）间的均衡性，其目的如下：
$${\mathcal{L}}_{\text{ring }}=\frac{1}{2n}\sum _{i=1}^n{\left({\Vert T\left(x_i\right)\Vert }_2-R\right)}^2$$
式中：R为学习到的范数值。然而，Ring-style并不鲁棒，如果学习到的R较小，可能会导致模式崩溃。取而代之的是，Geman-McClure模型，最小化如下损失函数：
$${\mathcal{L}}_{\text{ring }}^{GM}=\frac{{\sum }_{i=1}^n{\left({\Vert T\left(x_i\right)\Vert }_2-R\right)}^2}{2n\beta +{\sum }_{i=1}^n{\left({\Vert T\left(x_i\right)\Vert }_2-R\right)}^2}$$
其中$\beta$是Geman -麦克卢尔模型的尺度因子。

以端到端的方式进行训练优化模型。使用Stochasitc Gradient Descent ( Kiefer等, 1952)或Adam ( Kingma & Ba , 2014)优化器迭代训练类和域解耦部分、MINE和重建部分。使用流行的神经网络( e.g. Le Net、Alex Net或Res Net)作为特征生成器G。详细的训练过程在算法1中给出。