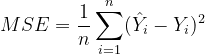动手学PaddlePaddle（1）：线性回归

你将学会：

• 机器学习的基本概念：假设函数、损失函数、优化算法
• 数据怎么进行归一化处理
• paddlepaddle深度学习框架的一些基本知识
• 如何用paddlepaddle深度学习框架搭建全连接神经网络

参考资料：https://www.paddlepaddle.org.cn/documentation/docs/zh/1.0/beginners_guide/quick_start/fit_a_line/README.cn.html

---

目录

1 - 线性回归的基本概念

2 - 训练阶段

2.1 - 引用库

2.2 - 数据

2.3 - 配置网络结构和设置参数

2.4 - 定义损失函数

2.5 - 优化方法

2.6 - 设置训练场所+创建执行器+参数初始化

2.7 - 开始训练

3 - 预测阶段

---

1 - 线性回归的基本概念

在线性回归中有几个基本的概念需要掌握：

• 假设函数（Hypothesis Function）
• 损失函数（Loss Function）
• 优化算法（Optimization Algorithm）

假设函数：

假设函数是指，用数学的方法描述自变量和因变量之间的关系，它们之间可以是一个线性函数或非线性函数。 在本次线性回顾模型中，假设函数为 ，其中，表示模型的预测结果（预测房价），用来和真实的Y区分。模型要学习的参数即：a,b。

损失函数：

损失函数是指，用数学的方法衡量假设函数预测结果与真实值之间的误差。这个差距越小预测越准确，而算法的任务就是使这个差距越来越小。立模型后，我们需要给模型一个优化目标，使得学到的参数能够让预测值尽可能地接近真实值Y。输入任意一个数据样本的目标值和模型给出的预测值,损失函数输出一个非负的实值。这个实值通常用来反映模型误差的大小。对于线性模型来讲，最常用的损失函数就是均方误差（Mean Squared Error， MSE）。

                                                                    

优化算法：

在模型训练中优化算法也是至关重要的，它决定了一个模型的精度和运算速度。本章的线性回归实例中主要使用了梯度下降法进行优化。

---

2 - 训练阶段

2.1 - 引用库

首先载入需要用到的库，它们分别是：

paddle.fluid：引入PaddlePaddle深度学习框架的fluid版本库；

numpy：NumPy是Python语言的一个扩展程序库。支持高端大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。NumPy的核心功能是"ndarray"(即n-dimensional array，多维数组)数据结构。

os: python的模块，可使用该模块对操作系统、目录、文件等进行操作。

matplotlib.pyplot：用于生成图，在验证模型准确率和展示成本变化趋势时会使用到。

import paddle
import paddle.fluid as fluid
import numpy as np
import os
import matplotlib.pyplot as plt

2.2 - 数据

BUF_SIZE=500
BATCH_SIZE=20

#用于训练的数据提供器，每次从缓存中随机读取批次大小的数据
train_reader = paddle.batch(
    paddle.reader.shuffle(paddle.dataset.uci_housing.train(), buf_size=BUF_SIZE), batch_size=BATCH_SIZE)   


#用于测试的数据提供器，每次从缓存中随机读取批次大小的数据
test_reader = paddle.batch(
    paddle.reader.shuffle(paddle.dataset.uci_housing.test(),buf_size=BUF_SIZE),batch_size=BATCH_SIZE)  

2.3 - 配置网络结构和设置参数

配置网络结构:

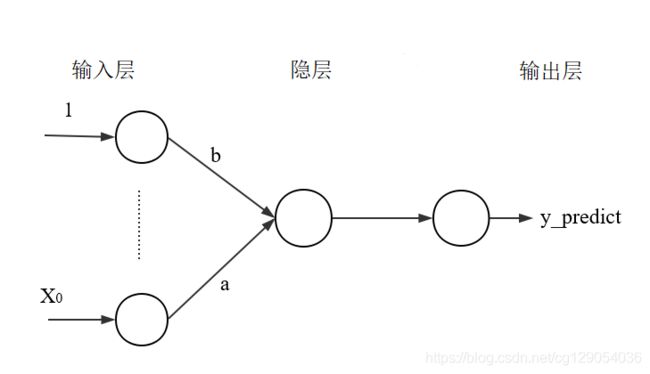
线性回归的模型其实就是一个采用线性激活函数（linear activation）的全连接层（fully-connected layer，fc_layer），因此在Paddlepaddle中利用全连接层模型构造线性回归，这样一个全连接层就可以看做是一个简单的神经网络，只包含输入层和输出层即可。本次的模型由于只有一个影响参数，因此输入只含一个。

输入层:
用 x = fluid.layers.data(name='x', shape=[13], dtype='float32')来表示数据的一个输入层，其中name属性的名称为"x"，数据的shape为13维向量，本次所用的房价数据集的每条数据有13个属性，所以shape=13。

输出层:
用y_predict = fluid.layers.fc(input=x, size=1, act=None)来表示输出层：其中paddle.layer.fc表示全连接层，input=x表示该层输入数据为x，size=1表示该层有一个神经元，在Fluid版本中使用的激活函数不再是调用一个函数了，而是传入一个字符串就可以，比如：act='relu'就表示使用relu激活函数。act=None表示激活函数为线性激活函数。

标签层:

用y = fluid.layers.data(name='y', shape=[1], dtype='float32')来表示标签数据，名称为y，有时我们名称不用y而用label。数据类型为一维向量。

#定义张量变量x，表示13维的特征值
x = fluid.layers.data(name='x', shape=[13], dtype='float32')
#定义张量y,表示目标值
y = fluid.layers.data(name='y', shape=[1], dtype='float32')
#定义一个简单的线性网络,连接输入和输出的全连接层
#input:输入tensor;
#size:该层输出单元的数目
#act:激活函数
y_predict=fluid.layers.fc(input=x,size=1,act=None)

2.4 - 定义损失函数

PaddlePaddle提供了很多的损失函数的接口，比如交叉熵损失函数(cross_entropy)。本项目是一个线性回归任务，所以使用的是均方差损失函数。可以调用fluid.layers.square_error_cost(input= ,laybel= )实现方差计算。因为fluid.layers.square_error_cost(input= ,laybel= )求的是一个Batch的损失值，所以还要通过调用fluid.layers.mean(loss)对方差求平均。

将输入定义为 房价预测值，label定义为 标签数据。进而计算损失值。

cost = fluid.layers.square_error_cost(input=y_predict, label=y) #求一个batch的损失值
avg_cost = fluid.layers.mean(cost)                              #对损失值求平均值

2.5 - 优化方法

损失函数定义确定后，需要定义参数优化方法。为了改善模型的训练速度以及效果，学术界先后提出了很多优化算法，包括： Momentum、RMSProp、Adam 等，已经被封装在fluid内部，读者可直接调用。本次可以用 fluid.optimizer.SGD(learning_rate= ) 使用随机梯度下降的方法优化，其中learning_rate表示学习率，大家可以自己尝试修改。

optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001)
opts = optimizer.minimize(avg_cost)

fluid有两个program，一个是default_main_program，一个是default_startup_program;

fluid.default_main_program()用于获取默认或全局main program(主程序)。该主程序用于训练和测试模型。fluid.layers 中的所有layer函数可以向 default_main_program 中添加算子和变量。

参数初始化操作会被写入fluid.default_startup_program();

使用fluid.default_main_program().clone(for_test=True)语句，我们可以克隆一个default_main_program，以备将来测试时使用。

2.6 - 设置训练场所+创建执行器+参数初始化

设置训练场所：
首先进行设置训练使用的设备。也就是选择是在CPU上进行训练，还是在GPU上进行训练。在复杂量较低的时候使用 CPU 就可以完成任务，但是对于大规模计算就需要使用 GPU 训练。目前 GPU 训练都是基于 CUDA 工具之上的。

代码实现也很简单，我们使用两行代码就可以实现，如下面所示：

• use_cuda=False 表示不使用 GPU 进行训练

创建执行器：
为了能够运行开发者定义的网络拓扑结构和优化器，需要定义执行器。由执行器来真正的执行参数的初始化和网络的训练过程。fulid使用了一个C++类Executor用于运行一个程序，Executor类似一个解释器，Fluid将会使用这样一个解析器来训练和测试模型。

之后run一下，初始化执行器； 配置完模型后，参数初始化操作会被写入到 fluid.default_startup_program() 中。 使用 fluid.Executor() 运行 这一程序，即可在全局中随机初始化参数。

#使用CPU训练
use_cuda = False
place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace() 

exe = fluid.Executor(place)              #创建一个Executor实例exe
exe.run(fluid.default_startup_program()) #Executor的run()方法执行startup_program(),进行参数初始化

接下来定义映射

输入网络的数据要与网络本身应该接受的数据相匹配。在paddle的 fluid 中使用 feed_list 的概念来保证输入的数据与网络接受的数据的顺序是一致的。本示例中使用 feed_list = [x,y] 来告知网络，输入的数据是分为两部分，第一部分是 x 值，第二部分是 label 值。

映射完之后，创建 DataFeeder 对象，在训练的时候，用户可调用其 feeder.feed(iterable) 方法将用户传入的iterable 数据转换为 LoDTensor。

# 定义feeder 
feeder = fluid.DataFeeder(place=place, feed_list=[x, y])#feed_list:向模型输入的变量名

2.7 - 开始训练

iter=0;
iters=[]
train_costs=[]

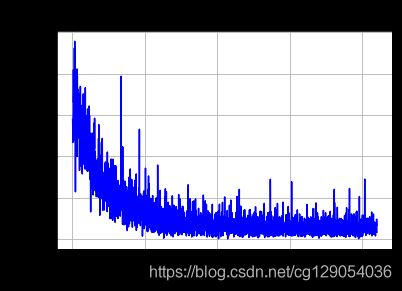
def plot_train_cost(iters,train_costs):
    title="training cost"
    plt.title(title, fontsize=24)
    plt.xlabel("iter", fontsize=14)
    plt.ylabel("cost", fontsize=14)
    plt.plot(iters, train_costs,color='blue',label='training cost') 
    plt.grid()
    plt.show()


EPOCH_NUM=100
model_save_dir = "/home/aistudio/data/model_save_dir/inference.model"

for pass_id in range(EPOCH_NUM):                                  #训练EPOCH_NUM轮
    # 开始训练并输出最后一个batch的损失值
    train_cost = 0
    for batch_id, data in enumerate(train_reader()):              #遍历train_reader迭代器
        train_cost = exe.run(program=fluid.default_main_program(),#运行主程序
                             feed=feeder.feed(data),              #喂入一个batch的训练数据，根据feed_list和data提供的信息，将输入数据转成一种特殊的数据结构
                             fetch_list=[avg_cost])     
        #print("Pass:%d, Cost:%0.5f" % (pass_id, train_cost[0][0]))    #打印最后一个batch的损失值
        iter=iter+BATCH_SIZE
        iters.append(iter)
        train_costs.append(train_cost[0][0])

   
    # 开始测试并输出最后一个batch的损失值
    test_cost = 0
    for batch_id, data in enumerate(test_reader()):               #遍历test_reader迭代器
        test_cost= exe.run(program=test_program, #运行测试cheng
                            feed=feeder.feed(data),               #喂入一个batch的测试数据
                            fetch_list=[avg_cost])                #fetch均方误差
    print('Test:%d, Cost:%0.5f' % (pass_id, test_cost[0][0]))     #打印最后一个batch的损失值
    
    #保存模型
    # 如果保存路径不存在就创建
    if not os.path.exists(model_save_dir):
        os.makedirs(model_save_dir)
    print ('save models to %s' % (model_save_dir))
    #保存训练参数到指定路径中，构建一个专门用预测的program
    fluid.io.save_inference_model(model_save_dir,   #保存推理model的路径
                                  ['x'],            #推理（inference）需要 feed 的数据
                                  [y_predict],      #保存推理（inference）结果的 Variables
                                  exe)              #exe 保存 inference model
plot_train_cost(iters,train_costs)

---

3 - 预测阶段

定义一个画图的函数，把预测结果展示出来

#先定两个list，用来存放预测结果、真实值；
infer_results=[]
groud_truths=[]

#绘制真实值和预测值对比图
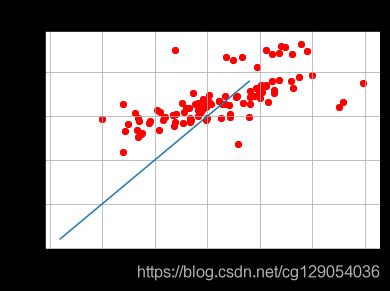
def plot_infer_result(groud_truths,infer_results):
    title='Boston'
    plt.title(title, fontsize=24)
    x = np.arange(1,20) 
    y = x
    plt.plot(x, y)
    plt.xlabel('ground truth', fontsize=14)
    plt.ylabel('infer result', fontsize=14)
    plt.scatter(groud_truths, infer_results,color='red',label='training cost') 
    plt.grid()
    plt.show()

#预测之前，我们需要创建预测用的Executor
infer_exe = fluid.Executor(place)    #创建推测用的executor
inference_scope = fluid.core.Scope() #Scope指定作用域

with fluid.scope_guard(inference_scope):#修改全局/默认作用域（scope）, 运行时的所有变量都将分配给新的scope。
    #从指定目录中加载 预测用的model(inference model)
    [inference_program,                             #推理的program
     feed_target_names,                             #需要在推理program中提供数据的变量名称
     fetch_targets] = fluid.io.load_inference_model(#fetch_targets: 推断结果
                                    model_save_dir, #model_save_dir:模型训练路径 
                                    infer_exe)      #infer_exe: 预测用executor
    #获取预测数据
    infer_reader = paddle.batch(paddle.dataset.uci_housing.test(),  #获取uci_housing的测试数据
                          batch_size=200)                           #从测试数据中读取一个大小为10的batch数据
    #从test_reader中分割x和label
    test_data = next(infer_reader())
    test_x = np.array([data[0] for data in test_data]).astype("float32") # 提取测试集中的x
    test_y= np.array([data[1] for data in test_data]).astype("float32")  # 提取测试集中的label
    results = infer_exe.run(inference_program,                              #预测模型
                            feed={feed_target_names[0]: np.array(test_x)},  #喂入要预测的x值
                            fetch_list=fetch_targets)                       #得到推测结果 
                            
    print("infer results: (House Price)")
    for idx, val in enumerate(results[0]):
        print("%d: %.2f" % (idx, val))
        infer_results.append(val)
    print("ground truth:")
    for idx, val in enumerate(test_y):
        print("%d: %.2f" % (idx, val))
        groud_truths.append(val)
    plot_infer_result(groud_truths,infer_results)