【数学建模笔记】【第七讲】多元线性回归分析(二):虚拟变量的设置以及交互项的解释,以及基于Stata的普通回归与标准化回归分析实例
温馨提示:
本文共有9683字,阅读并理解全文需要半小时左右
一、回归系数的解释
书接上文,上文谈到内生性的解决之后,我们对回归问题的探究还没有完。
比如下面这个问题:
我们说线性回归他的表达式可以是广义的,可以含有二次项,可以含有对数项,那么含有对数项的模型中的β怎么解释他的具体意义呢?
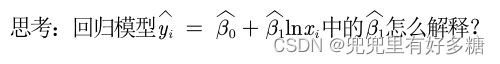
弄清楚这个问题之前,我们首先要明白什么情况下我们会偏向于对自变量进行取对数的处理:
伍德里奇的《计量经济学导论,现代观点》里,第六章176-177页有详细的论述;
取对数意味着原被解释变量对解释变量的弹性,即百分比的变化而不是数值的变化;
目前,对于什么时候取对数还没有固定的规则,但是有一些经验法则:
- 与市场价值相关的,例如,价格、销售额、工资等都可以取对数;
- 以年度量的变量,如受教育年限、工作经历等通常不取对数;
- 比例变量,如失业率、参与率等,两者均可;
- 变量取值必须是非负数,如果包含0,则可以对y取对数ln(1+y);
取对数的好处:
- 减弱数据的异方差性
- 如果变量本身不符合正态分布,取 了对数后可能渐近服从正态分布
- 模型形式的需要,让模型具有经济学意义。
以下是一些取对数情况的回归系数的解释:
一元线性回归: = + + ,x每增加1个单位,y平均变化b个单位:

半对数模型:=a+blnx+μ,x每增加1%,y平均变化b/100个单位:

半对数模型:=a+bx+μ,x每增加1个单位,y平均变化(100b)%:

对于多元回归模型,我们就加一句“在控制其他变量不变的情况下”,然后逐一的套用上面的话即可。
二、虚拟变量X
如果自变量中有定性变量,例如性别、地域等,在
回归中要怎么处理呢?
例如:我们要研究性别对于工资的影响(性别歧视)
方法就是将这个变量定义为一个虚拟变量,比如说定义female这个变量表示性别,然后取1表示女性,取0表示男性。

那么如何解释虚拟变量前面的那个回归系数呢?
方法如下图:
求y对female的期望之后,构造出这个回归变量,即可看出他的意义是:
在其他自变量给定的情况下,女性的平均工资与男性的平均工资的差异。

三、回归实例
现有某电商平台846条关于婴幼儿奶粉的销售信息,每条信息由11个指
标组成。其中,评价量可以从一个侧面反映顾客对产品的关注度。
请对所给数据进行以下方面的分析,要求最终的分析将不仅仅有益于
商家,更有益于宝妈们为宝贝选择适合自己的奶粉。
- 以评价量为因变量,分析其它变量和评价量之间的关系;
- 以评价量为因变量,研究影响评价量的重要因素
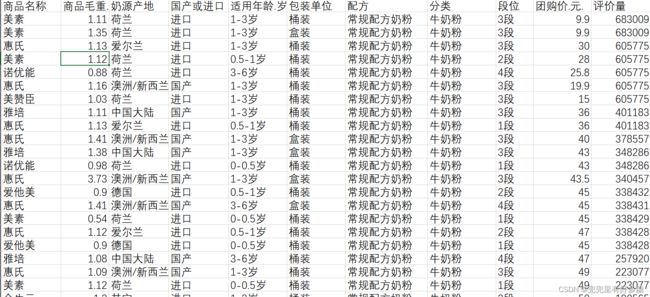
一般使用Stata这个软件进行回归分析比较方便。
关于Stata这个软件的安装有时间我会再写一篇指导安装的文章。
详情请看这篇文章:
【番外】Stata软件安装教程
下面我们直接应用:
首先我们导入需要的数据;
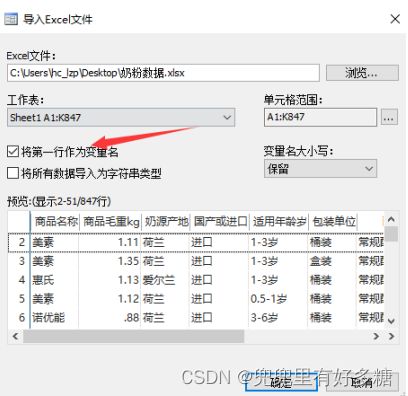
点击“确定”后软件会产生一行代码,我们只需把这行代码复制到控制台运行即可完成导入。
导入成功的标志就是右边的变量存储区会有变量显示出来:
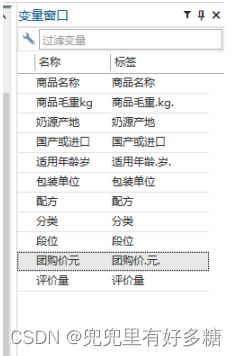
由于下面的控制台只负责运行代码,而不会保存代码。所以如果想将代码保存(就像Matlab的m文件一样),那么可以照如下操作:
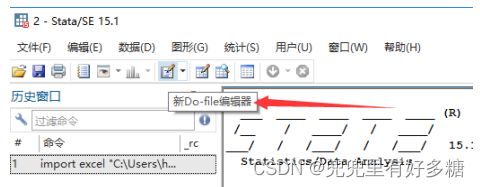
新建一个do文件,在新建的文件中粘贴刚才的代码,然后保存到你常用的路径中即可:
下次直接打开该do文件点击运行即可。
那么回到正题,我们将数据导入之后做什么呢?
Stata提供了丰富的函数供我们对数据进行处理:
Stata数据的描述性统计
1.定量数据
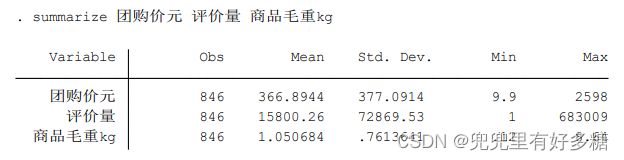
summarize 变量1 变量2 … 变量n
- 这后面的变量可以手写,也可以直接双击右侧变量区的变量直接添加
- summarize可以简写作sum,后面加变量名,也可以达到一样的效果
- 该函数只适用于对定量数据,即数值数据进行统计描述,一定不能把定性数据的变量放进去。
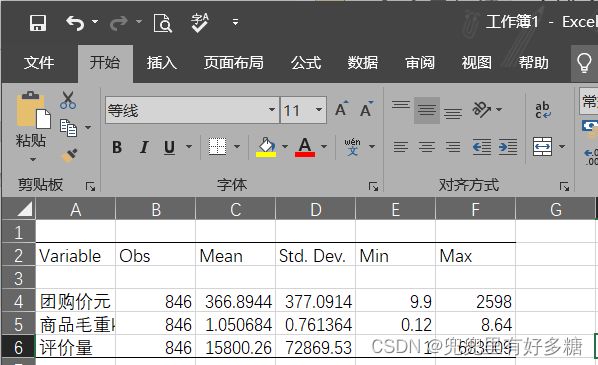
- 不要把结果直接截图放到论文中。因为在论文中会因为分辨率问题变得模糊,很影响论文观感。正确的做法是全选中这里给提供的表格,鼠标右击,点击”复制表格“,复制到Excel中美化一下,然后再复制到论文中。

2.定性数据
tabulate 变量名,gen(A)
返回对应的这个变量的频率分布表,并生成对应的虚拟变量(以A开头)
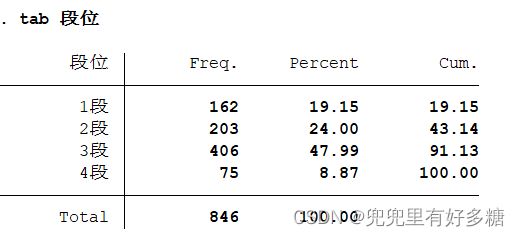
注:
- 后面的gen(A)可以加可以不加。
- 可以简写为tab
如果加上后面的gen(A)是什么效果呢?
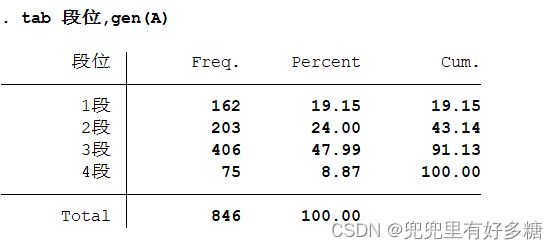
我们会发现统计描述部分并没有什么区别,但是再变量存储区部分,多了几个变量:

这些A1,A2等等就是刚刚产生的这些定性变量对应的虚拟变量。
我们可以浏览一下导入的数据来看到产生的变化:
点击下图所示的”数据浏览“按钮
进入到如下界面:
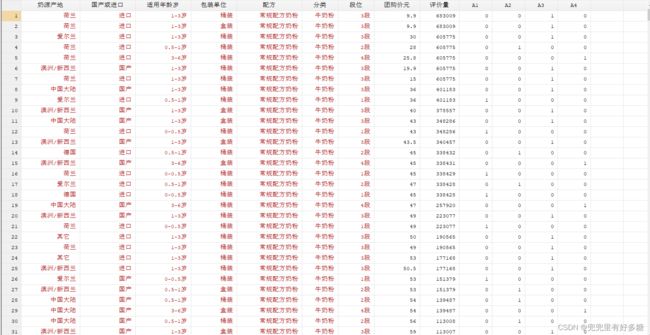
我们可以看到,除了我们的原始数据之外,又多了四列变量,分别是A1,A2,A3,A4。他们分别代表的是原先的定性变量”段位“的1段,2段,3段,4段。
何以见得?
比如下图:

这几个变量只在相应的段位后面显示1,其余都是0。代表了他们所显示的段位。结合我们讲过的虚拟变量的定义我们就能很清楚这个关系了。
3.Stata回归的语句
regress y x1 x2 … xk
(默认使用的OLS:普通最小二乘估计法)
(regress也可以简写为reg)
【例】
代码:regress 评价量 团购价元 商品毛重kg
结果:
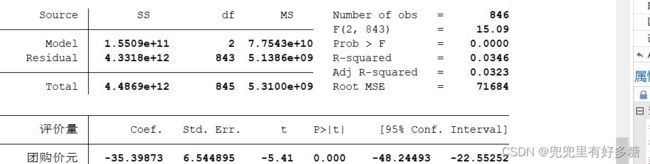
- Model:代表的是SSR:回归平方和
- Residual:代表SSE,误差平方和
- Total:SST
- df:自由度
- R-squared =1-SSR/SST
- MS=SS/df,是将SS按照自由度平均后的值,这个用的很少,一般不用考虑,一般用的是前面两项
样本的个数n是846个,那么SST的自由度就是n-1=845,SSR对应的自由度是等于k,SSE对应的自由度是n-k-1。
这个自由度是用来做什么的呢?是最后拟合调整拟合优度的。

这个F(2,843)是一个F统计量构造出来的。此F统计量他的第一个自由度是2,第二个自由度是843。实际上对应的就是SSR和SSE的两个自由度。其检验值等于15.09。
(你要看一个检验,首先一定要弄清楚这几个东西:原假设是什么,构造的统计量是什么:F统计量还是什么,还有就是对应的检验值的P值。)
那么此处的H0(原假设)是什么呢?
我们这里有K个自变量,这里的H0就是假设这K个自变量前面的回归系数全部都是0。
假如我们没有拒绝H0(也就是P值求出来比如说是0.3,他是大于0.05的),那就无法拒绝H0,那次是就要下结论:无法拒绝原假设,也就是认为K个变量的回归系数都是0,那此时就认为我们的回归没有多大意义。因为回归出来所有的系数都是0,所以这个模型就没有任何意义。
而此时我们看我们生成的数据:P值是0.0000,是明显小于0.05的,所以此时我们的回归是有意义的,回归系数不全为0。
还有就是这里既有R-squared,也有Adj R-squared,上面已经说了R-squared是如何计算的,这个参数叫做拟合优度,在有些情况下我们需要调整这个拟合优度,算出来的改进值就是Adj R-squared。
关于拟合优度:
- 回归分为解释型回归和预测型回归。 预测型回归一般才会更看重 R 2 R^2 R2。
解释型回归更多的关注模型整体显著性以及自变量的统计显著性和经济意义显著性即可。 - 对于预测型回归,如果 R 2 R^2 R2实在太低,可以对模型进行调整,例如对数据取对数或者平方后再进行回归。
- 数据中可能有存在异常值或者数据的分布极度不均匀也会导致 R 2 R^2 R2过小
- 补充:关于拟合优度和调整后的拟合优度: 我们引入的自变量越多,拟合优度会变大。但我们倾向于使用调整后的拟合优度,如果新引入的自变量对SSE的减少程度特别少,那么调整后的拟合优度反而会减小
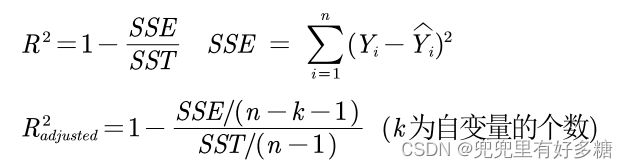
什么是预测型回归呢?就是你要建立一个模型比如:
y = β ^ 0 + β ^ 1 x 1 + β ^ 1 x 2 + … … + β ^ k x k \begin{align} y=\hat{\beta}_0+\hat{\beta}_1x_1+\hat{\beta}_1x_2+……+\hat{\beta}_kx_k \end{align} y=β^0+β^1x1+β^1x2+……+β^kxk
然后我们需要的是你通过模型去预测每一个y的具体值。这就是预测型回归,而解释型回归则是要求我们解释与每个自变量的关系,就像我们正在处理的这一题一样。
预测型回归更看重 R 2 R^2 R2,如果 R 2 R^2 R2太小,说明这个模型预测的y和实际的y相差很大。
而解释型回归更看中的是这个拟合模型中变量的显著性问题。
所以一般在论文中我们一般只用Adj R-squared就可以了。
后面的Root-MSE是均方误差,这个没有必要看。
对于下面这张表格:

由于我们的拟合模型是:
y = β ^ 0 + β ^ 1 x 1 + β ^ 1 x 2 \begin{align} y=\hat{\beta}_0+\hat{\beta}_1x_1+\hat{\beta}_1x_2 \end{align} y=β^0+β^1x1+β^1x2
Coef这一列就是回归系数。那么这个表格中的_cons表示的就是 β ^ 0 \hat{\beta}_0 β^0。
而 β ^ 1 \hat{\beta}_1 β^1表示的是团购价这个变量的回归系数,就是-35.39873这个值。而商品毛重的回归系数就是 β ^ 2 \hat{\beta}_2 β^2,就是2410.303了。第二列是回归系数对应的标准误差。这个标准误差的作用是构造第三列的t统计量的。t统计量就是回归系数除以标准误差构造出来的。具体为什么用t检验统计量,以及这个标准误差是怎么求的,我之后会单写一篇文章,这里不做说明。
这里我们只需要知道我们是用t检验统计量来检验回归系数的就可以了。而后面这一列是t统计量对应的P值。
这个值怎么看呢?现在我们有了回归系数,一般要对这个回归系数进行显著性检验:
原假设是H0:假定 β 1 \beta_1 β1等于0。(注意,此处我们假定的是 β 1 \beta_1 β1,而不是 β ^ 1 \hat{\beta}_1 β^1,因为 β ^ 1 \hat{\beta}_1 β^1是已知量,就是-35.39873,而 β 1 \beta_1 β1才是我们要通过 β ^ 1 \hat{\beta}_1 β^1去估计的量。所以假设的一定是未知量 β 1 \beta_1 β1)
然后构造出t这个统计量。发现P值是0.000,显然小于0.05,所以拒绝原假设,代表在95%置信水平下,该回归系数显著的异于0。
对于 β 2 \beta_2 β2来说,原假设也是假定其等于0,而 算出的P值为0.457,显著的大于0.05,所以我们无法拒绝原假设,也就是说 β 2 \beta_2 β2是等于0的。所以我们的 β ^ 2 \hat{\beta}_2 β^2即使等于2411.303这么大也无济于事,因为假设出来说明他不显著,分析他也没有多大的意义。这就是显著性分析带给我们的信息,即:把那些不显著的变量不予考虑。那么照这样的说法我们可以看出_cons这个变量无疑还是显著的。
最后这一列是置信区间,我们一般不太关注这里的数值。一般只用前面的回归系数即可。
那么上述这些都是对定量数据的回归分析,如何对定量数据作定性分析呢?
那么我们可以输入如下这段带有定性变量的代码:regress 评价量 配方,但是发现无法运行,显示没有可用的变量:
这是因为“配方”是定性变量,他的变量都是文字类型,无法识别。所以就用到我们刚才讲的tabulate函数,将定性变量转化成虚拟变量。然后再用虚拟变量进行回归分析即可。
(小技巧:生成虚拟变量后,在变量窗口中按住Shift不放,可同时选中一列,然后再直接拖动到输入区域)
我们输入如下代码: regress 评价量 G1 G2 G3 G4,然后可看到结果就出来了。
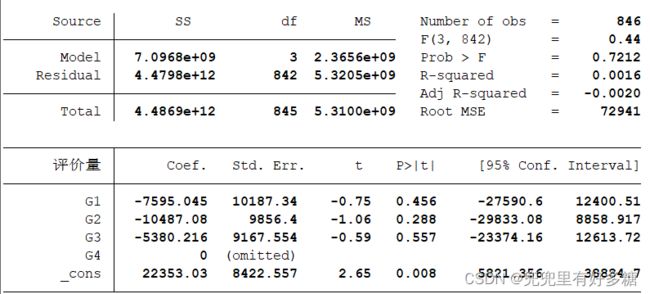
但是有一行提示:
note: G4 omitted because of collinearity
并且我们看到表中的G4这一项的回归系数是0,这是为什么呢?
因为定性变量这种多变量问题,会存在多重共线性问题,在回归的时候应该挑选变量数目n-1个变量进行回归分析,而不是把n个全部拿来分析。所以势必有一个变量就变成了供其他变量进行对照的变量。在这里,Stata随机选择了G4作为其他变量的对照变量进行回归分析。也就是Stata会自动检测数据的完全多重共线性问题并帮我们解决。
那么这个表中的数据应该怎么看呢?
其实很简单,每一个变量的回归系数已经不是绝对的数值了,而是相对于G4的0来比较的。比如:G1的 -7595.045 其实是G1-G4的值,除了这个值的来源有变化,其他都和上面所讲的是一样的。
接下来我们就将所有的变量放入回归分析中:
regress 团购价元 评价量 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5
> E1 E2 E3 E4 F1 F2 G1 G2 G3 G4
首先看上半部分是对回归模型整体的分析,上半部分的右边那张表是对回归模型进行显著性检验。
我们看到F统计量的P值是0.0000,明显小于0.05。所以说明该统计模型是有意义的。
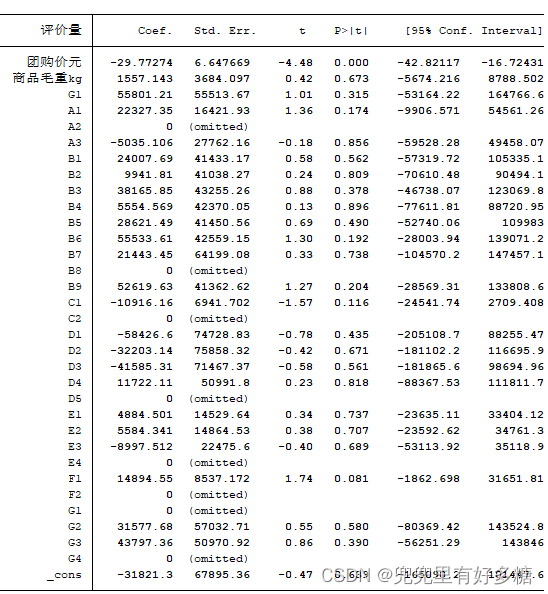
接下来关注回归系数,可以先找一下下面那张表中有哪些回归系数是显著的。
我们可以发现如下图框起来的这两个变量对应的回归系数的P值较小,团购价这一项的P值小于0.05,那么他是在95%的置信水平之下是显著的,而F1这一项要求放宽一点,因为他比0.05稍大一点,基本上满足在90%的置信水平之下是显著的。

那么接下来对这些显著的变量进行解释,不显著的变量就不用解释了。
比如“团购价”代表:在其他变量不变的情况下,当团购价每增加一元,会导致评价量平均减少29.77274条。
比如F1代表:由于F1是“分类”里面的“牛奶粉
“的虚拟变量,并且F2是那个因多重共线性忽略的基准变量,是0。所以F1代表在其他变量不变的情况下,分类为牛奶粉的评价量要比分类为羊奶粉的评价量多14894.55条。
![]()
这就是我们这一道题的第一问。
关于第一问还有一些问题要讨论:
我们如何把这些生成的回归参数的表格放入论文中呢?如果直接放的话可以放在附录里边,因为比较冗长。但是实际上这个表格中很多信息我们是不需要的。此时就可以用Stata自带的一种函数生成另一个表格:
由于这个功能其实是一个插件,所以使用之前需要先安装。
所以先运行以下这行代码安装这个功能:
ssc install reg2docx, all replace
如果出现这样的报错:
cannot write in directory C:\Users\����\ado
用下面的方式可以解决,亲测有效:1.找到你安装的软件的文件夹,里面有ado、docs等文件夹。
2.检查ado文件夹里面有没有puls子文件夹,没有的话建立一个。
3.打开stata,创建一个do文档,输入下面的命令。
sysdir set PLUS " plus文件夹的路径 " // 外部命令的存放位置 并将该do文档保存到安装软件的文件夹里面(与ado、docs等文件夹并列),命名为profile.do
4.创新打开stata,下载命令。
安装好之后运行如下代码:
//下面这一行就是回归的语句,如果之前运行过,此处可以不重复运行
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4
//下面这行语句是把上面回归产生的结果保存到名为m2的文件中
est store m2
//下面这行语句是把m2文件中的内容用我们刚刚安装的那个插件reg2docx 来重新处理生成一张我们想要的表格
reg2docx m2 using m2.docx, replace
代码运行完之后如图所示:

我们点击红色框中部分打开生成的表格:

打开后全选,先点击宋体,然后点击”New Time Romans“,这样就可以把所有的汉字变为宋体,所有的英文变为New Time Romans,然后我们在表格的结尾加这么一句话:*** p<0.01 ** p<0.05 * p<0.1

来有效的展现出显著性水平的区分。
这张表比刚才那张表要简洁许多,我们可以直接放在附录中。
OK,到此为止我们开始讨论第二问:

看题目要求就是要确定这些变量之间谁最重要。那就需要运用到另一种回归:就是标准化回归。
什么是标准化回归?
简单来说就是去量纲后的回归(因为你要比较不同变量之间的显著性的大小,那么带着量纲怎么比,所以先把量纲去掉,然后再比较)
官话:为了更为精准的研究影响评价量的重要因素(去除量纲的影响),我们可考虑使用标准化回归系数。
那么如何进行标准化回归呢?
对数据进行标准化,就是将原始数据减去它的均数后,再除以该变量的标准差,计算得到新的变量值,新变量构成的回归方程称为标准化回归方程,回归后相应可得到标准化回归系数。 标准化系数的绝对值越大,说明对因变量的影响就越大(只关注显著的回归系数哦,不显著的我们没必要进行比较)
那如何在Stata中实现标准化回归呢?
Stata标准化回归命令
regress y x1 x2 … xk,beta
(1)为什么常数项没有标准化回归系数?
常数的均值是其本身,其标准差是0,求不出来标准化的数。
(2)为啥和之前的回归结果完全相同,除了多了最后那一列标准化回归系数?
对数据进行标准化处理不会影响回归系数的标准误,也不会影响显著性.
那么我们在原来的回归代码基础上演示一遍标准化回归:
写入代码:
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4,beta
得到如下的表格:

可以发现后边多了一行Beta值,其余的和之前的表格没有任何差别。
我们只需要看显著的自变量即可(此处只有两个变量是显著的,就是“团购价格”和“F1”)
团购价格对应的Beta系数的绝对值是0.15,而F1对应的Beta的绝对值是0.06。
因为0.06<0.15,所以可以看出“团购价”是影响更显著的那个变量。
最终全部代码如下:
// 按键盘上的PageUp可以使用上一次输入的代码(Matleb中是上箭头)
// 清除所有变量
clear
// 清屏 和 matlab的clc类似
cls
// 导入数据(其实是我们直接在界面上粘贴过来的,我们用鼠标点界面导入更方便 本条请删除后再复制到论文中,如果评委老师看到了就知道这不是你写的了)
// import excel "C:\Users\hc_lzp\Desktop\数学建模\第7讲.多元回归分析\代码和例题数据\课堂中讲解的奶粉数据.xlsx", sheet("Sheet1") firstrow
import excel "课堂中讲解的奶粉数据.xlsx", sheet("Sheet1") firstrow
// 定量变量的描述性统计
summarize 团购价元 评价量 商品毛重kg
// 定性变量的频数分布,并得到相应字母开头的虚拟变量
tabulate 配方,gen(A)
tabulate 奶源产地 ,gen(B)
tabulate 国产或进口 ,gen(C)
tabulate 适用年龄岁 ,gen(D)
tabulate 包装单位 ,gen(E)
tabulate 分类 ,gen(F)
tabulate 段位 ,gen(G)
// 下面进行回归
regress 评价量 团购价元 商品毛重kg
// 下面的语句可帮助我们把回归结果保存在Word文档中
// 在使用之前需要运行下面这个代码来安装下这个功能包(运行一次之后就可以注释掉了)
// ssc install reg2docx, all replace
// 如果安装出现connection timed out的错误,可以尝试换成手机热点联网,如果手机热点也不能下载,就不用这个命令吧,可以自己做一个回归结果表,如果觉得麻烦就直接把回归结果截图。
est store m1
reg2docx m1 using m1.docx, replace
// *** p<0.01 ** p<0.05 * p<0.1
// Stata会自动剔除多重共线性的变量
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4
est store m2
reg2docx m2 using m2.docx, replace
// 得到标准化回归系数
regress 评价量 团购价元 商品毛重kg, b
// 画出残差图
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4
rvfplot
// 残差与拟合值的散点图
graph export a1.png ,replace
// 残差与自变量团购价的散点图
rvpplot 团购价元
graph export a2.png ,replace
// 为什么评价量的拟合值会出现负数?
// 描述性统计并给出分位数对应的数值
summarize 评价量,d
// 作评价量的概率密度估计图
kdensity 评价量
graph export a3.png ,replace
// 异方差BP检验
estat hettest ,rhs iid
// 异方差怀特检验
estat imtest,white
// 使用OLS + 稳健的标准误
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4, r
est store m3
reg2docx m3 using m3.docx, replace
// 计算VIF
estat vif
// 逐步回归(一定要注意完全多重共线性的影响)
// 向前逐步回归(后面的r表示稳健的标准误)
stepwise reg 评价量 团购价元 商品毛重kg A1 A3 B1 B2 B3 B4 B5 B6 B7 B9 C1 D1 D2 D3 D4 E1 E2 E3 F1 G1 G2 G3, r pe(0.05)
// 向后逐步回归(后面的r表示稳健的标准误)
stepwise reg 评价量 团购价元 商品毛重kg A1 A3 B1 B2 B3 B4 B5 B6 B7 B9 C1 D1 D2 D3 D4 E1 E2 E3 F1 G1 G2 G3, r pr(0.05)
// 向后逐步回归的同时使用标准化回归系数(在r后面跟上一个b即可)
stepwise reg 评价量 团购价元 商品毛重kg A1 A3 B1 B2 B3 B4 B5 B6 B7 B9 C1 D1 D2 D3 D4 E1 E2 E3 F1 G1 G2 G3, r b pr(0.05)
// 补充语法 (大家不需要具体的去学Stata软件,掌握我课堂上教给大家的一些命令应对数学建模比赛就可以啦)
// 事实上大家学好Excel,学好后应对90%的数据预处理问题都能解决
// (1) 用已知变量生成新的变量
generate lny = log(评价量)
generate price_square = 团购价元 ^2
generate interaction_term = 团购价元*商品毛重kg
// (2) 修改变量名称,因为用中文命名变量名称有时候可能容易出现未知Bug
rename 团购价元 price
// 注意:代码文件仅供参考,一定不要直接用于自己的数模论文中
// 国赛对于论文的查重要求非常严格,代码雷同也算作抄袭
在运行以下几步时又延伸出一个问题:
// 定量变量的描述性统计
summarize 团购价元 评价量 商品毛重kg
// 定性变量的频数分布,并得到相应字母开头的虚拟变量
tabulate 配方,gen(A)
tabulate 奶源产地 ,gen(B)
tabulate 国产或进口 ,gen(C)
tabulate 适用年龄岁 ,gen(D)
tabulate 包装单位 ,gen(E)
tabulate 分类 ,gen(F)
tabulate 段位 ,gen(G)
运行完这段之后我们就把需要分析的所有定性变量,定量变量都描述分析完了,并且生成了对应的虚拟变量。


如何把这些数据放入论文中呢?如果把他们都复制到论文中,显得太过冗余(因为真的很多),一种办法是放在附录中,还有一种办法是用Excel进行画图,用这种简练的方式把所有的数据呈现出来,既美观又显得丰富。
这个我会在另一篇文章里介绍怎么用Excel画数据透视图。
【番外】利用Excel表格绘制数据透视图
这一期就到这里啦!!!
下一期再演示一个例题!!!