【图学习】GNN GCN图学习技术概述

此篇博客是对中科院计算所沈华伟博士的图学习报告笔记。B站上有上传的视频：https://www.bilibili.com/video/av667610549/

参考：https://blog.csdn.net/Frank_LJiang/article/details/94888011?utm_medium=distribute.pc_relevant.none-task-blog-OPENSEARCH-3.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-3.control

目录

一、图学习基础

1.1拉普拉斯矩阵

1.2拉普拉斯算子

1.3 卷积

二、谱方法

2.1 spectral CNN

2.2 ChebyNet

2.3 沈华伟团队Graph Wavelet Neural Network

三、空间方法

3.1 By analogy

3.2 GraphSAGE 

3.3 GCN: Graph Convolution Network

3.4 GAT: Graph Attention Network

3.5 MoNet: A general framework for spatial methods

四、其他内容

4.1谱方法和空间方法区别与联系

4.2 图信号处理（滤波）

4.3 图池化Graph Pooling

五、开放讨论

5.1 图的结构特性真的发挥了实质性的作用了吗：

5.2 CNN究竟是做的什么工作。是一个上下文表示学习？

5.3 未来的应用

---

一、图学习基础

1.1 拉普拉斯矩阵

是图的度矩阵，是图的邻接矩阵。图的拉普拉斯矩阵矩阵表示了图的导数，刻画了信号在图上的平滑程度。
普通形式的拉普拉斯矩阵：

矩阵元素为：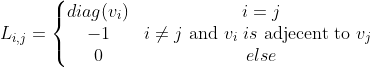

对称归一化的拉普拉斯矩阵（Symmetric normalized Laplacian）（最常用）：

矩阵元素为：

随机游走归一化拉普拉斯矩阵（Random walk normalized Laplacian）：

矩阵元素为：

无向图的拉普拉斯矩阵性质
（1）拉普拉斯矩阵是半正定矩阵。（最小特征值大于等于0）
（2）特征值中0出现的次数就是图连通区域的个数。
（3）最小特征值是0，因为拉普拉斯矩阵（普通形式： ）每一行的和均为0，并且最小特征值对应的特征向量是每个值全为1的 向量；;
（4）最小非零特征值是图的代数连通度。

拉普拉斯矩阵特征分解：，
是列向量为拉普拉斯矩阵单位特征向量的矩阵。

1.2 拉普拉斯算子

拉普拉斯算子(Laplacian operator) 的物理意义是空间二阶导，准确定义是：标量梯度场中的散度，一般可用于描述物理量的流入流出。 比如说在二维空间中的温度传播规律，一般可以用拉普拉斯算子来描述。拉普拉斯矩阵也叫做离散的拉普拉斯算子。拉普拉斯算子是n维欧几里德空间中的一个二阶微分算子，定义为梯度∆f的散度∇ ⋅ ∇f 。因此如果f是二阶可微的实函数，则f的拉普拉斯算子∆定义为：。f的拉普拉斯算子也是笛卡尔坐标系所有非混合二阶偏导数：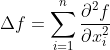

函数f的拉普拉斯算子也是该函数的海塞矩阵(是一个多元函数的二阶偏导数构成的方阵)的迹：

1.3 卷积

CNN等神经网络的成功原因之一就是能够学习到一些局部化的网络结构，在通过堆叠变成结构化的模式。这也得益于卷积的平移不变性。所以，图卷积神经网络就是把欧式空间拓展到非欧空间。在图上定义卷积，由于复杂网络的节点度的分布是重尾分布，节点的分布结构有很大的不同。所以早期的图神经网络的研究主要集中在如何定义图上的卷积和图上的池化操作上。卷积就是图上的信号处理。一维连续函数卷积运算：


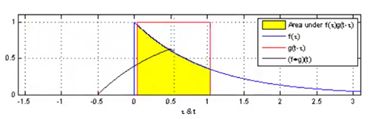
离散卷积：

二、谱方法

GCN从开始就存在两种定义方法：谱方法和空间方法。谱方法是空间方法的一种子集，是一种特殊的空间方法。谱方法试图在谱域定义卷积而不是原始的节点域。传统欧式空间里的CNN在图像上定义卷积，是在图像的空间域上定义子模板。因此直观考虑的话，也是想在Graph的节点域中定义子模版。但是由于节点域上的卷积不满足平移不变性，所以无法直接在节点域中定义卷积操作。为此，便考虑将节点域变换到谱域，在谱域上实现卷积的操作，然后从谱域转换到节点域。

空间方法就是坚持在空间域上定义卷积。空间方法面临的问题就是每个节点的邻居节点数量是不同的，就难以定义一个固定大小的邻域实现参数共享。但是其卷积的基本思想还是存在的：即每个节点在其邻域中节点的加权平均。其主要问题就是如何解决参数共享，GCN、GAT等方法就是解决参数共享的问题，跟谱方法不是一个思路。下面先从谱方法开始梳理。

2.1 spectral CNN

图卷积神经网络的输入：，是节点集合，是边的集合，是加权的邻接矩阵。是节点个数。每个节点有个特征，个节点就有个特征，是节点的特征矩阵。的每一列（此向量有n个元素）就是定义在图上的节点的一个信号。图上的信号的定义：假设一个图有个节点，每个节点有一个取值，那么一个信号就是一个维向量。我们把这个维向量信号变换到谱域去就需要一组基。这个基就是拉普拉斯矩阵特的n个正交的特征向量。卷积就是把一个信号投影到这个基上，就是和做内积把投影到上。是拉普拉斯矩阵特的特征向量为列向量组成的矩阵。所以信号在谱域上的表达就是（图傅里叶变换）。在谱域的表达转换为原始的节点域的表达就是（图傅里叶逆变换）。

谱域的卷积定义是基于卷积定理的：即两个信号的卷积，可以看成两者傅里叶变换后的点积。所以对于一个信号先进行傅里叶变换投影到谱空间去，然后把卷积核信号也投影到谱域，在谱域内做点积。在点积后做傅里叶逆变换回过来，这样的一个过程就实现了谱域的卷积定义。而在实际的操作上，整体被看作谱域的卷积核（或者卷积滤波器convolution filter），最原始的spectral CNN里的是参数为的对角阵。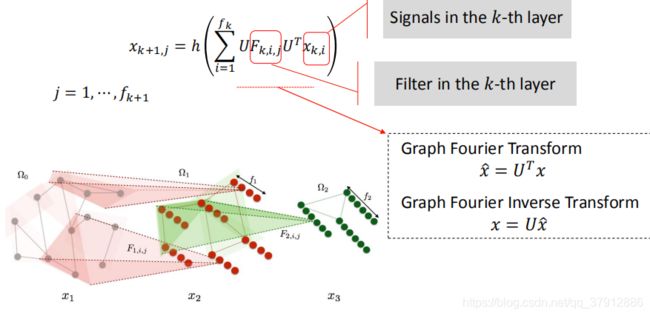

因此，谱域上的卷积定义可以分为三步：第一步把信号进行傅里叶变换，第二步就是进行卷积运算（在谱域进行卷积），第三步就是傅里叶逆变换。（下图中是点积运算）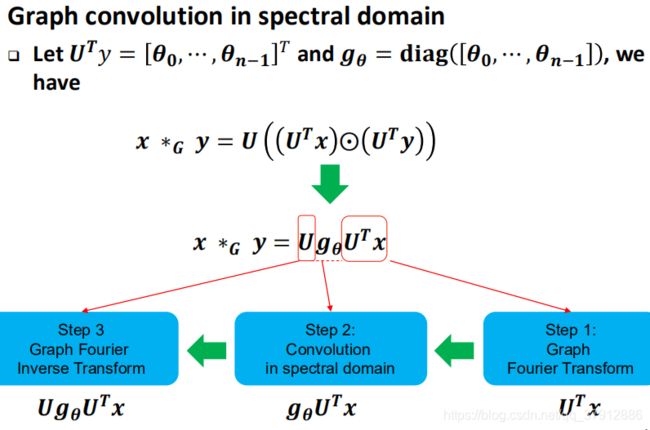

这个谱方法的定义就到此结束了。但是这种方法存在三个比较大的问题：
1、依赖于拉普拉斯矩阵特的特征矩阵的分解，计算困难
2、对信号进行傅里叶变换的时候，是一个稠密的矩阵成以一个向量，计算困难
3、没有做到localized，即影响某一个信号的其它节点是来自于其他的所有信号而不是这个信号的邻域

对上述三个问题的解决就是谱方法的发展方向

2.2 ChebyNet

2016年提出的ChebyNet就是把谱域上的卷积核进行了参数化: 把有个自由参数的对角阵转换为有个参数的对角阵

 

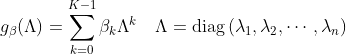
因此ChebyNet的卷积操作就变成了：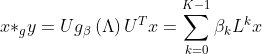

相比于最原始的图卷积方法改善点如下：减少了自由参数的数量；不需要特征分解了，L是稀疏的；是localized的，只受到K跳邻居的影响。有了这种方法以后，GCN才开始使用。

2.3 沈华伟团队Graph Wavelet Neural Network

B. Xu, H. Shen, Q. Cao, Y. Qiu, X. Cheng. Graph wavelet neural network. ICLR 2019.

接下来介绍沈华伟团队做的工作：图小波神经网络。

第一个变化：由于式子中的会带来很多问题比如稠密，而且不具备localization的特性，所以把傅里叶变换的基换成小波基。傅里叶变换的基在时域上是正弦函数，在图上也是周期性的函数。小波基是只在局部有信号，其他地方都是0的波。所以小波变换的天生优势有：本身稀疏，本身localized，计算代价低。小波的基实际上是一个局部的信号，刻画目标节点距离其他节点的远近程度。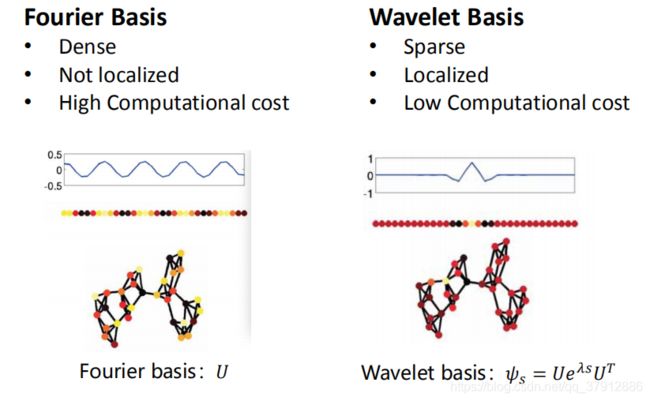

原始的图神经网络的傅里叶基换成小波基：

 

图小波神经网络：（下式的为激活函数）


参数的复杂度为：，是节点的个数,  是输入信号维度，是输出信号的维度。

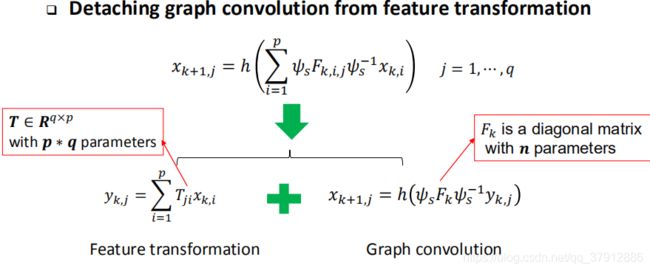
第二个变化：把图的卷积和特征变换拆成两步进行。参数的复杂度从变为了：

三、空间方法

3.1 By analogy

M. Niepert, M. Ahmed, K. Kutzkov. Learning Convolutional Neural Networks for Graphs. ICML, 2016.
采用类比的方法把CNN从图像上迁移到Graph上。

卷积的三步操作中，只有第一步是需要平移不变性的支持，后面两个步骤是不需要的。所以，对于每一个节点，根据节点距离的度量选择固定个数的节点作为中心节点的邻居，然后进行排序（比如按照距离的远近程度）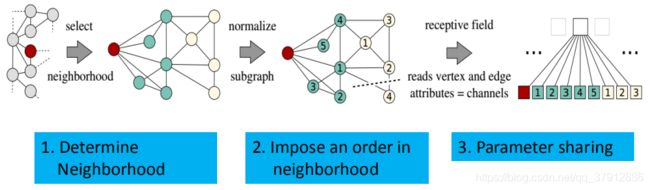

3.2 GraphSAGE 

W. L. Hamilton, R. Ying, J. Leskovec. Inductive Representation Learning on Large Graphs. NeuraIPS 2017

GraphSAGE以目标节点为中心，随机游走的方式来选择固定个数的邻居节点（选择自己周围的节点的概率较大）。然后进行聚合、拼接，从而实现卷积。至此，卷积的概念就变成了aggregate & combine的过程。

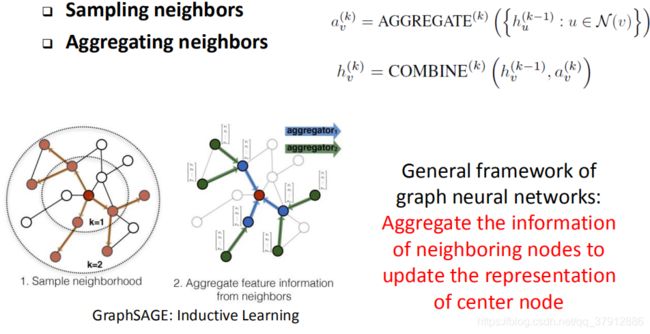
3.3 GCN: Graph Convolution Network

T. N. Kipf, and M. Welling. Semi-supervised classification with graph convolutional networks. ICLR 2017

 

可以看作谱方法的一个特例也是空间方法的起点。把自己的一阶邻居的特征变换一下拿过来聚合一下就完了，实际上并没有卷积的操作。权重没有参数，而是拉普拉斯矩阵特直接定义的。类似于图上的平滑、或者图上的半监督学习。

 

3.4 GAT: Graph Attention Network

P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio, Y. Bengio. Graph Attention Networks. NeuraIPS 2018

GAT认为GCN没有卷积过程，只是在做特征变换的时候使用了参数共享，参数传递使用的是拉普拉斯矩阵。所以矩阵只用来做了特征变换。所以GAT在两个部分都进行了参数共享：1、特征变换参数 2、加入了注意力attention参数，即收到周围节点信息的时候共享出去的时候的参数。GAT认为卷积核的参数就是这个参数。如右下的图，把自身节点做完Feature Transformation然后把邻居节点也做Feature Transformation，再把两者combine，过一个attention机制活得自身的权重。这个权重是卷积得到的，而不是使用拉普拉斯矩阵直接编码得到的。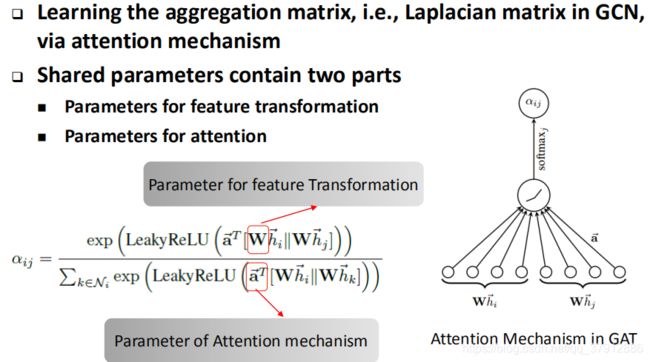

3.5 MoNet: A general framework for spatial methods

F. Monti, D. Boscaini, J. Masci, E. Rodola, J. Svoboda, M. M. Bronstein. Geometric deep learning on graphs

and manifolds using mixture model CNNs. CVPR 2017.

MoNet定义了多个用来度量目标节点和其他节点相似度的核函数，卷积核的每个参数就是对应的核函数的权重。

四、其他内容

4.1谱方法和空间方法区别与联系

空间方法就是需要一个空间上的核函数，每一个核函数就是度量了节点之间相似度。所谓的卷积就是对这些不同相似度定义方式的加权平均。所以核函数才是需要定义的基础。核函数在谱方法里就是谱变换的基，在空间方法里就是要选择的哪些邻居节点。卷积核是这些核函数的权重。这是空间方法一般性的思想。

谱方法和空间方法的异同：
 

联系：谱方法是空间方法的特例，是有显示变换空间的空间方法。

区别：
谱方法需要显式地定义卷积核，空间方法不需要显式的定义。在定义谱方法的时候，我们需要明确知道要把节点投影到哪个空间内。比如使用傅里叶变换，就是把节点投影到拉普拉斯矩阵特征向量定义的空间，如果使用小波变换，就是投影到小波空间。但是使用空间方法的时候不需要知道投影到的空间是什么空间，只需要知道卷积核矩阵是什么。

如下图所示，Spectral CNN的卷积核矩阵（Kernel）就是，卷积核的参数就是。

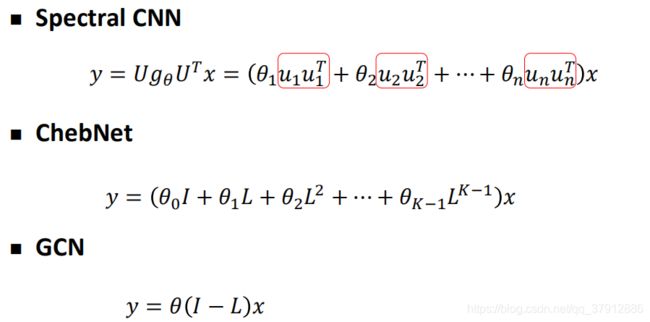
GCN比较特殊，虽然只有一个参数，但实际表现比Spectral CNN和ChebNet好。

 

4.2 图信号处理（滤波）

对于节点分类等任务需要特别关注图上信号的平滑问题。信号是图上各个节点的取值，关于这个图的平滑度可以用下试表达：

把上式里的换成特征向量，就是特征值。所以特征值就表示了对应的特征向量关于这个图的平滑程度。拉普拉斯矩阵有一个对应特征值为0的，特征向量元素为1的特征向量，这个特征向量标志着一个平滑信号，即每个节点的取值都一样，所以它的平滑程度是最好的。所以把基本滤波器定义为，对于一个信号，基本滤波器只让中的频率成分为的分量通过：

所以，图上的每个卷积操作就是一系列基础滤波器的组合，这就决定了什么组成频率的信号能够通过这个卷积。因此，卷积又被称为过滤器、滤波器filter，在数学上就是一个信号处理的过程。

标准的Spectral CNN是基础滤波器的线性组合：

ChebNet的方法可以看成这组线性组合使用了特殊的系数。ChebNet认为，信号的频率越高，其赋予的信号的权重就越大，所以ChebNet对高频信号有增强特性（高通特性），抑制了低频信号，这对节点的分类并没有帮助作用，所以ChebNet效果不如GCN。GCN相比只考虑了的两种情况，避免了对基础滤波器的非线性增益情况。

因此，沈华伟等人，直接设计低通滤波器，对高频信号实现一个指数衰减效果，从而实现图的平滑性的刻画，从而更好的过滤和检测信号。

B. Xu, H. Shen, Q. Cao, K. Cen, X. Cheng. Graph Convolutional Networks using Heat Kernel for Semi-supervised Learning,

IJCAI 2019

|
下图展示了谱方法的特性：Spectral CNN是一个均匀滤波器，ChebNet是高通滤波器，GCN是对ChebNet的低阶近似（0阶和1阶）。沈华伟等人提出的Graphheat则是直接构造了低通滤波器。

邻居节点选择的问题是空间方法的根本问题。邻居节点的选择依赖于邻居节点相似度的度量方法。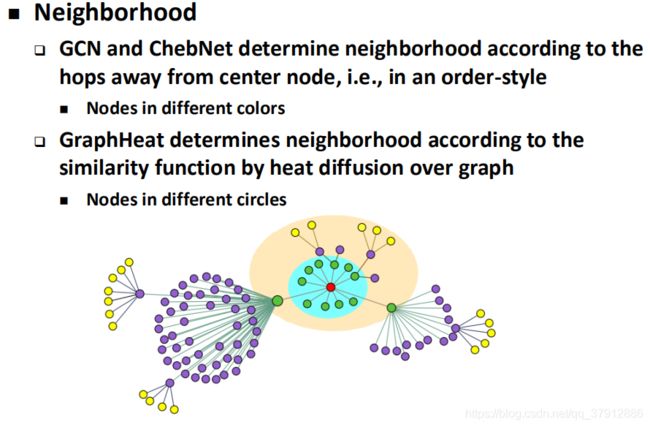

4.3 图池化Graph Pooling

图卷积定义完毕后，GCN网络定义的就比较完备了。由于早期图上的任务都是节点级别的，例如链路预测和节点分类，只需要卷积不需要池化，所以Pooling没有得到重视。如果需要处理图级别的任务，比如图分类问题，或者信号分类，那就需要Pooling。ChebNet在提出的时候尝试给过池化的方法。图的池化可以大概分为两类：

图粗化Graph coarsening（即下采样down sampling）：先把节点进行聚类，然后把每一类作为一个超级节点super node，最后一个图可以变成一个节点。节点的merge可以实现做好，或者在GCN训练的过程中学习，例如DiffPooling。
Ying, R., You, J., Morris, C., Ren, X., Hamilton, W. L., and Leskovec, J. Hierarchical graph representation learning with differentiable pooling, NeuraIPS 2018

节点选择（Node selection）：做完一层卷积之后，根据节点的重要性选择一些具有代表性的节点来代表整层的网络。所以Node selection需要事先预设或者在训练中学习一种节点重要性矩阵。这个重要性选择的思想其实在前面基于类比的空间方法里就有了。
J. Lee, I. Lee, J. Kang. Self-attention Graph Pooling, ICML 2019.

所以，无论是粗化还是节点选择都需要assignment matrix。这个矩阵表示的是某个节点属于某个类别的可能系有多大。assignment matrix可以是硬性的网络划分，也可以是软聚类。这个矩阵设置好或者学好，那么池化的工作就基本完成了。目前对Pooling的研究处于探索阶段，下采样变化的空间也比较小。下采样方法的争议也比较大，到底是依赖于图的结构还是信号特征也没统一的定义。

五、开放讨论

5.1 图的结构特性真的发挥了实质性的作用了吗：

GCN学习到的是网络节点上信号的Pattern，而不是图结构本身的pattern。CNN尽管在图像上有很好的效果，但并不意味着在图数据上用到了图本身的结构。因此无论是GCN还是GNN，图的结构只是起到了平滑和聚合的作用，真正起到作用的还是节点上的特征。或者是节点临近性或者节点结构相似性的体现。谱方法和结构方法虽然做了尝试，但是实际上都没有显式地抽出结构特征。

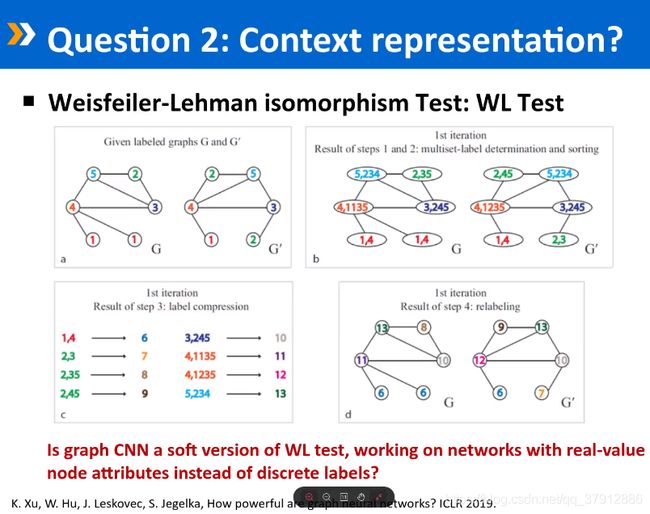
5.2 CNN究竟是做的什么工作。是一个上下文表示学习？

K. Xu, W. Hu, J. Leskovec, S. Jegelka, How powerful are graph neural networks? ICLR 2019.

5.3 未来的应用

Node-level现在用的很多了；
Graph-level现在用还是很少，典型场景有根据蛋白质节点结构进行分类；
Signal-level是CNN原始的应用场景，比如图像的分类和检测问题。在Graph领域上，是指的图的结构不变，节点信号变化。典型的应用有路网交通流量预测。

图上的频谱分析是图信号处理里重要的一块内容。所需要的频率和任务密切相关。如果是节点分类任务，利用网络的平滑性。使用的是低频信号。如果做异常检测，使用的往往是高频信号（比如用来fake image检测，机器生成的图往往在高频部分有较大瑕疵）。

现在很多使用GAN对抗生成网络用来生成图。

以后的发展：如何把GCN做的更大，层数更多。