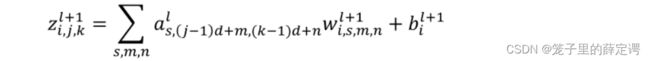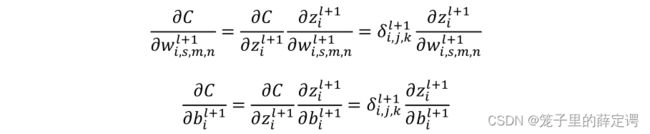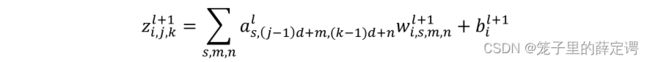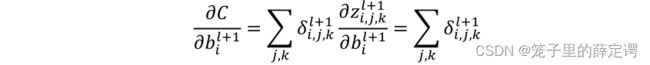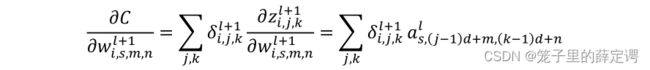NNDL 作业7：第五章课后题（1×1 卷积核 | CNN BP）

目录

第五章课后题（1×1 卷积核 | CNN BP）

 习题5-2 证明宽卷积具有交换性，即公式(5.13)

习题5-3 分析卷积神经网络中使用1×1卷积核作用

习题5-4 对于一个输入为100×100×256的特征映射组,使用3×3的卷积核,输出为100×100×256的特征映射组的卷积层,求其时间和空间复杂度.如果引入一个1×1卷积核,先得到100 × 100×64的特征映射,再进行3×3的卷积,得到100 ×100×256的特征映射组,求其时间和空间复杂度.

习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系

CNN反向传播（数学推导+numpy手撸）

 总结

---

第五章课后题（1×1 卷积核 | CNN BP）

 习题5-2 证明宽卷积具有交换性，即公式(5.13)

背景知识：

 

推导过程：

 

 参考老师PPT(就是把老师的PPT数字换成了一堆字母)：

习题5-3 分析卷积神经网络中使用1×1卷积核作用

In Convolutional Nets, there is no such thing as “fully-connected layers”. There are only convolution layers with 1x1 convolution kernels and a full connection table. – Yann LeCun

根据吴恩达老师和网上博客讲的，总结一下作用：

1.升维/降维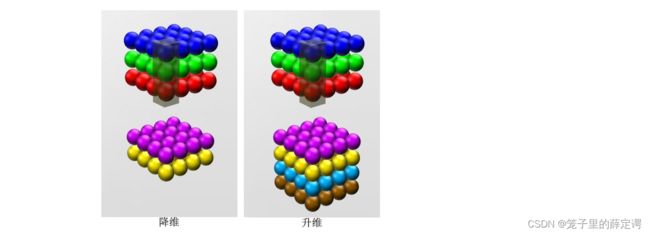
​
  可以想象到的是1×1的卷积对于单通道输入是没有意义的，因为1×1卷积并不会修改输入的高和宽，只会修改通道数或者保持通道数不变的同时增加网络的深度，添加非线性。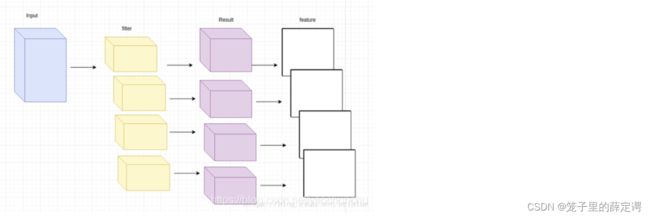
​

我们可以直观地感受到卷积过程中：卷积后的的 featuremap 通道数是与卷积核的个数相同的.

所以，如果输入图片通道是 3，卷积核的数量是 6 ，那么生成的 feature map 通道就是 6，这就是升维，如果卷积核的数量是 1，那么生成的 feature map 只有 1 个通道，这就是降维度。
注：所有尺寸的卷积核都可以达到这样的目的。

2.减少网络参数和计算量
Inception模块举例：
在Inception网络中图像输入进来后，通常可以选择直接使用像素信息(1x1卷积)传递到下一层，可以选择3x3卷积，可以选择5x5卷积，还可以选择max pooling的方式downsample刚被卷积后的feature maps。 但在实际的网络设计中，究竟该如何选择需要大量的实验和经验的。 Inception就不用我们来选择，而是将4个选项给神经网络，让网络自己去选择最合适的解决方案。但是这些卷积滤波器的设计也会在计算上造成很大的消耗，由于3*3卷积或者5*5卷积在几百个filter的卷积层上做卷积操作时相当耗时，所以1*1卷积在3*3卷积或者5*5卷积计算之前先降低维度。
Inception模块结构图如下：
​
Incption模块图像输入、输出以及卷积核参数量：

输入feature map	卷积核大小(卷积核参数)	通道数	个数	卷积操作所生成的通道数	输出feature map
28*28*192	1*1	192	64	64	28*28*64
28*28*192	3*3	192	128	128	26*26*128
28*28*192	5*1	192	32	32	24*24*32

所以Inception模块左侧的输入参数量为：(1×1×192×64) + (3×3×192×128) + (5×5×192×32) = 153600，提取的特征图维度为：64+128+32+192 = 416
Inception模块右侧的输入参数量为:(1×1×192×64)+(1×1×192×96+3×3×96×128)+(1×1×192×16+5×5×16×32)+(1x1x32)=15904，提取的特征图维度为：64+128+32+32=256
由此可得，Inception模块加入1*1卷积降低维度的同时大幅减少了参数量

下面是吴恩达老师的计算量对比：

​

 ​
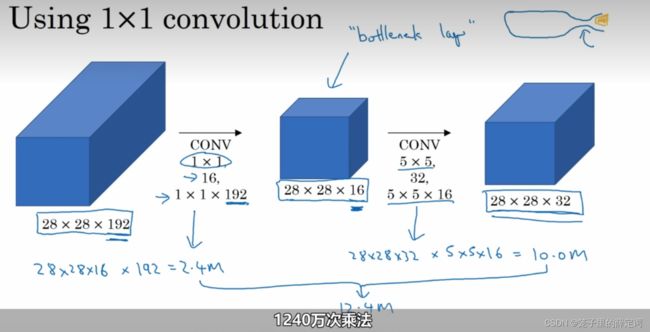
可以看到在Inception模块加入1*1卷积层大约降低了1/10的计算量。

3.增加网络的深度，添加非线性

增加网络的深度：直观上来讲，加 1 层1*1卷积，网络深度自然会增加。但问题的关键是增加网络的深度有什么好处？为什么非要用 1x1 来增加深度呢，难道其他形状卷积核不合适吗？
    这涉及到感受野的问题，卷积核越大，卷积提取的特征图 上单个节点的感受野就越大，随着网络深度的增加，越靠后的特征图上的节点感受野也越大。因此特征也越来越形象，也就是更能看清这个特征是个什么东西。层数越浅，就越不知道这个提取的特征到底是个什么东西。

添加非线性：想在不增加感受野的情况下，让网络加深，为的就是引入更多的非线性。而 1x1 卷积核，恰巧可以办到。卷积后生成图片的尺寸受卷积核的大小和卷积核个数影响，但如果卷积核是 1x1 ，个数也是 1，那么生成后的图像长宽不变，通道数为1。但通常一个卷积层是包含激活和池化的。也就是多了激活函数，比如 Sigmoid 和 Relu。

所以，在输入不发生尺寸的变化下，加入卷积层的同时引入了更多的非线性，这将增强神经网络的表达能力。

参考链接：16 - 2.5网络中的网络及1x1卷积_哔哩哔哩_bilibili
17 - 2.6初始网络动机_哔哩哔哩_bilibili
卷积神经网络CNN中1×1卷积作用理解_青衫憶笙的博客-CSDN博客_在cnn中使用1*1卷积时
卷积神经网络中1*1卷积的作用_m0_61899108的博客-CSDN博客
1*1卷积核的作用_nefetaria的博客-CSDN博客_1*1卷积核的作用
https://arxiv.org/pdf/1409.4842.pdf

习题5-4 对于一个输入为100×100×256的特征映射组,使用3×3的卷积核,输出为100×100×256的特征映射组的卷积层,求其时间和空间复杂度.如果引入一个1×1卷积核,先得到100 × 100×64的特征映射,再进行3×3的卷积,得到100 ×100×256的特征映射组,求其时间和空间复杂度.

1.时间复杂度：​

空间复杂度：100*100*256=2，560，000

2.时间复杂度：​
空间复杂度：64*100*100+256*100*100=3，200，000

从这一题也可以验证上一题的结论，加入1*1的卷积核会大大减少计算量(时间复杂度)，但是从计算结果也可以看出空间复杂度变大了，有点空间换时间的意思。

参考链接：邱锡鹏《神经网络与深度学习》—— 部分习题答案整理_小笠凹的博客-CSDN博客_神经网络与深度学习课后习题
《神经网络与深度学习-邱锡鹏》习题解答 - 知乎
 

习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系

​
参考链接：
(2条消息) 卷积神经网络前向及反向传播过程数学解析_恩泽君的博客-CSDN博客_卷积神经网络原理前向传播
卷积神经网络中卷积运算的前向传播与反向传播推导 - 腾讯云开发者社区-腾讯云 (tencent.com)
神经网络与深度学习[邱锡鹏] 第五章习题解析 - whyaza - 博客园 (cnblogs.com)
 

CNN反向传播（数学推导+numpy手撸）
 

误差传播：
参数更新规则：梯度下降法，公式如下：

定义误差项δ，如下：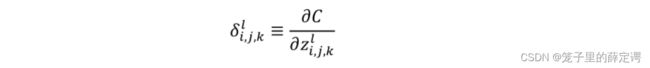

其中

l代表卷积神经网络第l层， j、k表示其特征向量第j行，第k列。w表示权重，i对应下一层神经元特征向量个数，s代表上一层特征向量个数，m、n表示一个卷积核第(m,n)个的值，b为偏置，z为该层神经元输入，a为该层神经元输出。
由链式求导法则，得误差传播过程为：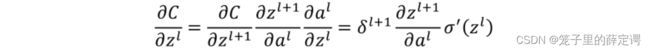

 这里主要是求第二项的值，但是这里又跟全连接网络不一样，不是简单的权重的转置。为了观察运算规律，刘建平老师给了一个很容易理解的例子：

结合上面公式，得误差传递公式：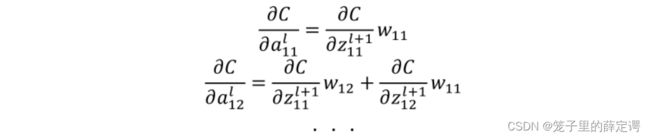


总结得出运算规律：a11在左上角,只参与了卷积运算1次，赋值给了z11；a12参与了两次卷积运算分别赋值给了z11和z12等；。那么求z11对a11的偏导我们就只需要求z11处误差对其的偏导；求对a12的偏导我们需要求对z11和z12处误差对其的偏导和，也就是要对其两个做运算，以此类推。
为了符合上面的运算规律，需要对误差第l+1层误差矩阵做补零操作，即将其周围添加宽度为n-1的0：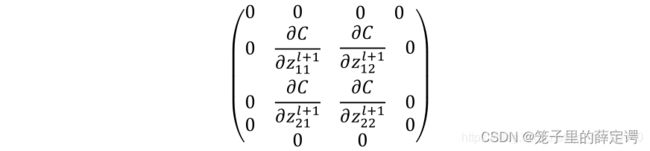

但是如果直接拿其与卷积核参数相乘，会发现移位现象，即z11项误差相乘的是w22而不是上面得w11，所以这时候就需要用到180°旋转变换，即：

 得到误差传播方程为：

继续总结运算规律：先要将对于上一层z的误差矩阵周围用0扩展,扩展尺寸为卷积核的大小n减去1，然后将卷积核旋转180°，最后就是跟卷积层前向传播一样的卷积操作。
即反向传播公式为：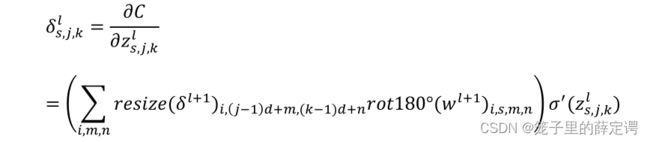

写成矩阵形式，得：

 参数更新：

根据链式求导法则和误差传播过程，得：

结合上面得前向传播公式：

不难得出：

 我在这里只进行了卷积层和卷积层之间的误差传播和参数更新过程，其实还有全连接层和卷积层层、池化层和卷积层的误差传播和参数更新(因为卷积网络不止有卷积层和卷积层的连接，池化层不用说肯定涉及到，在网络结构的最后也可能会涉及到全连接层和卷积层的连接)，我没有进行推导。
但是，全连接层和卷积层的误差传播和参数更新过程就是前馈神经网络的反向传播过程，在前面的学习都推烂了，池化层和卷积层的误差传播和参数更新过程刘建平老师讲的很好，链接如下：
卷积神经网络(CNN)反向传播算法 - 刘建平Pinard - 博客园
如果想有一个完整的反向传播过程，可以把全连接层和卷积层 以及 池化层和卷积层的误差传播和参数更新加到反向传播过程的前面，也不难。

numpy手撸：
这一部分是吴恩达老师DeepLearning.ai的课程作业，参考的优秀作业的写法：

import numpy as np
def padding(X, pad):
    X_pad = np.pad(X, (
        (0, 0),
        (pad, pad),
        (pad, pad),
        (0, 0)),
         mode='constant', constant_values=(0, 0))
    return X_pad
def conv_single_step(a_slice_prev, W, b):
    s = np.multiply(a_slice_prev, W)
    Z = np.sum(s)
    Z = Z + float(b)
    return Z
def conv_forward(A_prev, W, b, hparameters):
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    (f, f, n_C_prev, n_C) = W.shape
    stride = hparameters['stride']
    pad = hparameters['pad']
    n_H = int((n_H_prev + 2 * pad - f) / stride) + 1
    n_W = int((n_W_prev + 2 * pad - f) / stride) + 1
    Z = np.zeros((m, n_H, n_W, n_C))
    A_prev_pad = padding(A_prev, pad)

    for i in range(m):  # 依次遍历每个样本
        a_prev_pad = A_prev_pad[i]  # 获取当前样本
        for h in range(n_H):  # 在输出结果的垂直方向上循环
            for w in range(n_W):  # 在输出结果的水平方向上循环
                # 确定分片边界
                vert_start = h * stride
                vert_end = vert_start + f
                horiz_start = w * stride
                horiz_end = horiz_start + f

                for c in range(n_C):
                    a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
                    weights = W[:, :, :, c]
                    biases = b[:, :, :, c]
                    Z[i, h, w, c] = conv_single_step(a_slice_prev, weights, biases)

    assert (Z.shape == (m, n_H, n_W, n_C))
    mask = (A_prev, W, b, hparameters)

    return Z, mask

def backward(theta, mask):
    (A_prev, W, b, hparameters) = mask
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    (f, f, n_C_prev, n_C) = W.shape
    stride = hparameters['stride']
    pad = hparameters['pad']
    (m, n_H, n_W, n_C) = theta.shape
    dA_prev = np.zeros_like(A_prev)
    dW = np.zeros_like(W)
    db = np.zeros_like(b)
    A_prev_pad = padding(A_prev, pad)
    dA_prev_pad = padding(dA_prev, pad)
    for i in range(m):
        a_prev_pad = A_prev_pad[i]
        da_prev_pad = dA_prev_pad[i]
        for h in range(n_H):
            for w in range(n_W):
                for c in range(n_C):
                    vert_start = h * stride
                    vert_end = vert_start + f
                    horiz_start = w * stride
                    horiz_end = horiz_start + f
                    a_slice = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
                    da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:, :, :, c] * theta[i, h, w, c]
                    dW[:, :, :, c] += a_slice * theta[i, h, w, c]
                    db[:, :, :, c] += theta[i, h, w, c]
        dA_prev[i, :, :, :] = da_prev_pad[pad:-pad, pad:-pad, :]
    assert (dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
    return dA_prev, dW, db

A_prev = np.random.randn(10, 4, 4, 3)
W = np.random.randn(2, 2, 3, 8)
b = np.random.randn(1, 1, 1, 8)
hparameters = {"pad": 2,
               "stride": 2}
Z, mask_conv = conv_forward(A_prev, W, b, hparameters)
dA, dW, db = backward(Z, mask_conv)
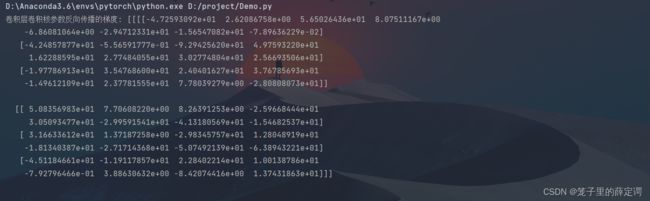
print("卷积层卷积核参数反向传播的梯度:", dW)
print("卷积层偏置项反向传播的梯度:", db)

 运行结果:

import numpy as np
def mask1(x):
    mask = (x == np.max(x))
    return mask
def distribute_value(dz, shape):
    (n_H, n_W) = shape
    average = dz / (n_H * n_W)
    a = np.ones(shape) * average
    return a
def pool_forward(A_prev, hparameters, mode="max"):
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    f = hparameters["f"]
    stride = hparameters["stride"]
    # 计算输出数据的维度
    n_H = int(1 + (n_H_prev - f) / stride)
    n_W = int(1 + (n_W_prev - f) / stride)
    n_C = n_C_prev
    # 定义输出结果
    A = np.zeros((m, n_H, n_W, n_C))
    # 逐个计算，对A的元素进行赋值
    for i in range(m):  # 遍历样本
        for h in range(n_H):  # 遍历n_H维度
            # 确定分片垂直方向上的位置
            vert_start = h * stride
            vert_end = vert_start + f

            for w in range(n_W):  # 遍历n_W维度
                # 确定分片水平方向上的位置
                horiz_start = w * stride
                horiz_end = horiz_start + f

                for c in range(n_C):  # 遍历通道
                    # 确定当前样本上的分片
                    a_prev_slice = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c]
                    # 根据池化方式，计算当前分片上的池化结果
                    if mode == "max":  # 最大池化
                        A[i, h, w, c] = np.max(a_prev_slice)
                    elif mode == "average":  # 平均池化
                        A[i, h, w, c] = np.mean(a_prev_slice)

    # 将池化层的输入和超参数缓存
    cache = (A_prev, hparameters)

    # 确保输出结果维度正确
    assert (A.shape == (m, n_H, n_W, n_C))

    return A, cache


def pool_backward(dA, cache, mode="max"):
    (A_prev, hparameters) = cache

    stride = hparameters['stride']
    f = hparameters['f']

    m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape
    m, n_H, n_W, n_C = dA.shape

    # 对输出结果进行初始化
    dA_prev = np.zeros_like(A_prev)

    for i in range(m):  # 遍历m个样本
        a_prev = A_prev[i]

        for h in range(n_H):  # 在垂直方向量遍历
            for w in range(n_W):  # 在水平方向上循环
                for c in range(n_C):  # 在通道上循环
                    # 找到输入的分片的边界
                    vert_start = h * stride
                    vert_end = vert_start + f
                    horiz_start = w * stride
                    horiz_end = horiz_start + f

                    # 根据池化方式选择不同的计算过程
                    if mode == "max":
                        # 确定输入数据的切片
                        a_prev_slice = a_prev[vert_start:vert_end, horiz_start:horiz_end, c]
                        # 创建掩码
                        mask = mask1(a_prev_slice)
                        # 计算dA_prev
                        dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += np.multiply(mask, dA[i, h, w, c])

                    elif mode == "average":
                        # 获取da值， 一个实数
                        da = dA[i, h, w, c]
                        shape = (f, f)
                        # 反向传播
                        dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += distribute_value(da, shape)

    assert (dA_prev.shape == A_prev.shape)

    return dA_prev


np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache =pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)

dA_prev = pool_backward(dA, cache, mode = "max")
print("============最大池化========")
print('反向传播梯度 ', dA)
dA_prev = pool_backward(dA, cache, mode = "average")
print("===========平均池化========")
print('反向传播梯度', dA)

 运行结果:

 总结

手推了关于卷积神经网络的理论知识并且参考吴恩达老师DeepLearning.ai课程优秀作业，使用numpy手撸了卷积神经网络前向传播和反向传播过程，收获很大。

总结了关于使用1×1卷积核的优点，之前在ResNet网络结构和Inception模块中见过这个尺寸的卷积核并且也知道它的部分优点，但从来没有认真研究过这个卷积核，这次查了很多资料，应该算对1×1这个尺寸的卷积核知根知底了。