（C语言）树的前中后序遍历-递归+非递归整理

目录

题目链接

参考

树的结构的定义

树的遍历思想

前序遍历

中序遍历

后序遍历

1.递归算法

1.1 前序遍历

1.2 中序遍历

1.3 后序遍历

2 迭代

2.1 C语言栈的创建

2.2 前序遍历

2.2.1 思想

2.2.2 代码

2.2 中序遍历

2.2.1 思想

2.2.2 代码

2.3 后序遍历

2.3.1 思想

2.3.2 代码

---

题目链接

力扣
力扣
力扣

参考

官方题解 
+
力扣

树的结构的定义

/**  
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 * 
 */

树的遍历思想

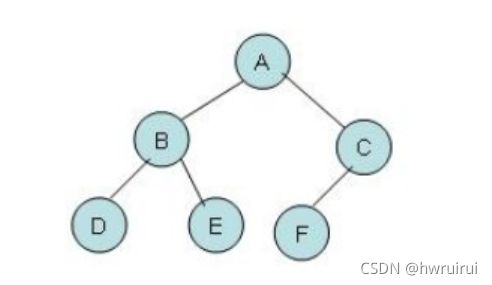
给这样一棵树：

前序遍历

        即从根节点出发，先遍历左子树，再遍历右子树。

        因此该树的前序遍历序列为：A B D E C F

中序遍历

        从树的根节点出发至最左的结点，然后以左子树->根节点->右子树的顺序遍历。

        因此该树的中序遍历序列为：D B E A F C

        规律：将树压扁至一个平面，（左子树一定在根节点左侧，右子树一定在根节点右侧）则刚好为中序遍历的序列，如果是二叉搜索树，中序遍历序列刚好是一个递增序列。

后序遍历

        以左子树->右子树->根节点的顺序遍历。

        因此该树的后序遍历序列为：D E B F C A

可以根据上面的算法引出递归的写法，思想非常简单，代码几乎相同，只不过遍历的顺序略有改变。

1.递归算法

1.1 前序遍历

void preorder(struct TreeNode* root, int* res, int* resSize) {
    if (!root) {
        return;
    }
    res[(*resSize)++] = root->val;
    preorder(root->left, res, resSize);
    preorder(root->right, res, resSize);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    int* res = malloc(sizeof(int) * 2000);
    *returnSize = 0;
    preorder(root, res, returnSize);
    return res;
}

1.2 中序遍历

void midorder(struct TreeNode* root, int* res, int* returnSize){
    if(!root)
        return;
    midorder(root->left, res, returnSize);
    res[(*returnSize)++] = root->val;
    midorder(root->right, res, returnSize);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    int * res = (int *)malloc(sizeof(int) * 2000);
    *returnSize = 0;
    midorder(root, res, returnSize);
    return res;
}

1.3 后序遍历

void backorder(struct TreeNode* root, int* res, int* returnSize) {
    if (!root) {
        return;
    }
    backorder(root->left, res, returnSize);
    backorder(root->right, res, returnSize);
    res[(*returnSize)++] = root->val;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    int* res = malloc(sizeof(int) * 2000);
    *returnSize = 0;
    backorder(root, res, returnSize);
    return res;
}

2 迭代

2.1 C语言栈的创建

        迭代的方法不可避免地需要使用到栈，所以定义一些栈的基础操作，后面方便使用，包括初始化、压栈、弹栈。

（其实可以不需要完整定义一个栈，对C语言来说，栈只是一个先进后出的思想，简便版可以看力扣官方题解，上面有链接~）

        先把代码放在这里

typedef struct{
    struct TreeNode* stk[2000];
    int top;
}Stack;
//定义一些栈的基础操作，后面方便使用，包括初始化、压栈、弹栈
Stack* create()
{
    Stack* S = (Stack*)malloc(sizeof(Stack));
    S->top = -1;
    return S;
}

void push(Stack* S, struct TreeNode* p)
{
    S->top++;
    S->stk[S->top] = p;
}

void pop(Stack* S)
{
    S->top--;
}

2.2 前序遍历

2.2.1 思想

        首先把根节点入栈。
        当栈不空的时候：
                1.弹栈顶元素node，并且输出该节点的值；
                2.如果node的右子树不为空，则压栈；
                3.如果node的左子树不为空，则压栈。
        压栈时先右后左的理由：
                前序遍历是根->左->右的顺序，所以左子树是后进先出。

2.2.2 代码

int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    *returnSize = 0;
    if(!root)
        return NULL;
    int * res = (int *)malloc(sizeof(int) * 100);   //遍历结果
    Stack* s = create();
    struct TreeNode* p;
    push(s, root); //把根节点入栈
    while(s->top > -1) //栈不空的时候
    {
        p = s->stk[s->top];
        res[(*returnSize)++] = p->val;
        pop(s);
        if(p->right)
        {
            push(s, p->right);
        }
        if(p->left)
        {
            push(s, p->left);
        }
    }
    return res;
}

2.2 中序遍历

2.2.1 思想

    首先将根节点入栈。
    将所有左孩子压栈。
    开始弹栈，每弹出一个栈顶元素node，如果它的右子树不为空，则重复上述操作

2.2.2 代码

int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if(!root)
        return NULL;
    int * res = (int *)malloc(sizeof(int) * 100);   //遍历结果
    Stack* s = create();
    struct TreeNode* p = root;
    while (p || s->top > -1)
    {
        while (p) 
        {
            push(s, p);
            p = p->left;
        }
        p = s->stk[s->top];
        res[(*returnSize)++] = p->val;
        pop(s);
        p = p->right;
    }
    return res;
}

2.3 后序遍历

2.3.1 思想

    与前序压栈顺序相同，只不过出栈顺序为：左->右->根
    每个节点需要记录是否被访问过
    如果flag = 0，说明未被访问过，改为1
    如果flag = 1，弹栈

2.3.2 代码

此处对栈做了一些小修改

首先是栈的定义

typedef struct{
    struct TreeNode* stk[2000];
    int flags[2000]; //加入了数组来对每个节点做标记
    int top;
}Stack;

在压栈时将flag都初始化为0

void push(Stack* S, struct TreeNode* p)
{
    S->top++;
    S->stk[S->top] = p;
    S->flags[S->top] = 0;
}

其他栈的操作代码不变

int *postorderTraversal(struct TreeNode *root, int *returnSize) {
    *returnSize = 0;
    if(!root)
        return NULL;
    int * res = (int *)malloc(sizeof(int) * 100);   //遍历结果
    Stack* s = create();
    struct TreeNode* p;
    push(s, root); //把根节点入栈
    while(s->top > -1) //栈不空的时候
    {
        p = s->stk[s->top];
        int flag = s->flags[s->top];
        if(flag)
        {
            res[(*returnSize)++] = p->val;
            pop(s);
        }
        else
        {
            s->flags[s->top] = 1;
            if(p->right)
                push(s, p->right);
            if(p->left)
                push(s, p->left);
        }
    }
    return res;
}