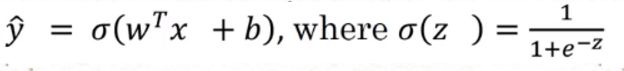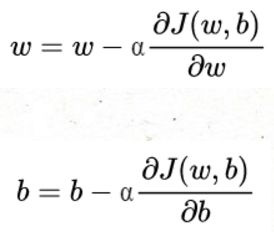吴恩达深度学习课程第一课 — 神经网络与深度学习
目录
1.神经网络(Neural Network)
1.1.神经网络
1.2.用神经网络进行监督学习(Supervised Learning with Neural Networks)
2.神经网络基础(Basics of Neural Network Programming)
2.1.逻辑回归(Logistic Regression)
2.2.损失函数(Loss Function)
2.3.梯度下降法(Gradient Descent)
2.4.计算流程图(Computation Graph)
2.5.逻辑回归中的梯度下降法(Logistic Regression Gradient descent)
2.6.向量化逻辑回归(Vectorizing Logistic Regression)
2.7.逻辑回归损失函数的解释(Explanation of logistic regression cost function)
3.1.神经网络表示(Neural Network Representation)
3.2.计算神经网络的输出(Computing a Neural Network's Output)
3.3.激活函数(Activation functions)
3.4.神经网络中的梯度下降算法(Gradient descent for Neural Networks)
3.5.随机初始化(Random Initialization)
4.深层神经网络(Deep Neural Networks)
4.1.深层神经网络(Deep Neural Networks)
4.2.为什么要用深层表示?(Why deep representations?)
4.3.前向和反向传播(Forward and backword functions)
4.4.参数及超参数(Parameters vs Hyperparameters)
4.5.这和大脑有什么关系?(Why does this have to do with the brain?)
1.神经网络(Neural Network)
1.1.神经网络
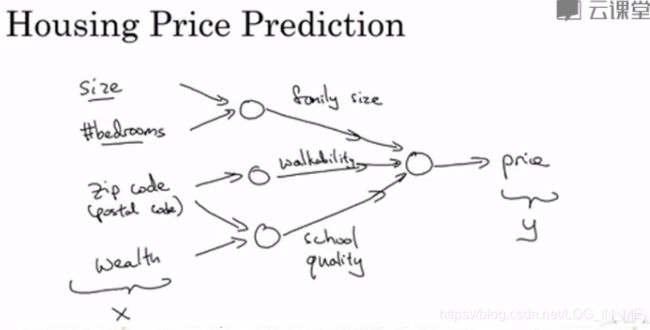
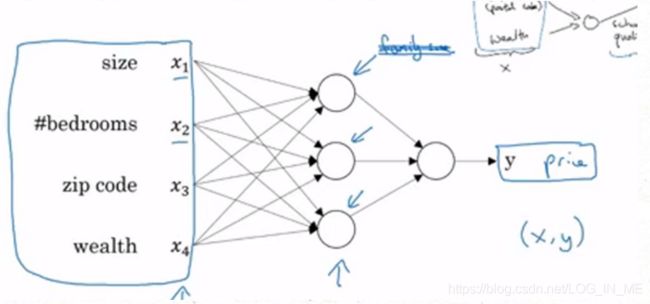
神经网络就是一些如下图所示的网络,输入一系列特征x,经过中间一系列小圆圈(函数)的计算,最终得到输出结果y。只要输入x,就能得到一个y。
对于中间的一些小圆圈,它们在神经网络中被称为隐藏单元(hidden units)。
1.2.用神经网络进行监督学习(Supervised Learning with Neural Networks)
对于一般的数据(房地产、广告产业),一般通常使用Standard NN(标椎的神经网络)
对于图像,经常使用CNN(卷积神经网络)
对于序列数据(音频、自然语言),经常使用RNN(循环神经网络)
对于更复杂的应用(无人驾驶),则需要更加Custom的混合神经网络
2.神经网络基础(Basics of Neural Network Programming)
2.1.逻辑回归(Logistic Regression)
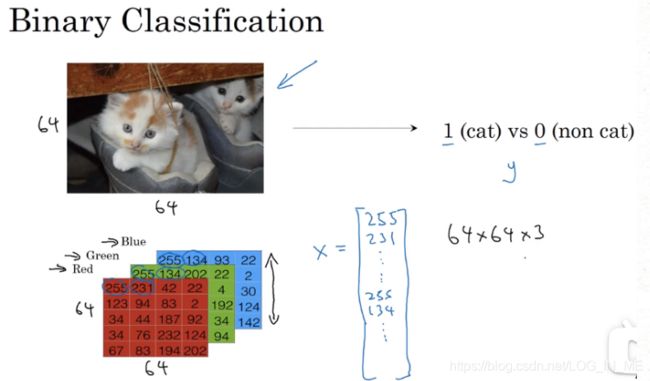
二分分类(Binary Classification):举个例子,如下图所示,给一个图像的特征向量x(RGB三通道每个像素值排列成一个向量),输出结果标签y=0或1,即表示图像中是否是一只猫。这样的结果为0或1的分类,叫二分分类。
logistic回归是一个用于二分分类的算法。logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求参数,其区别在于他们的因变量不同,多重线性回归直接将w‘x+b作为因变量,即y =w‘x+b,而logistic回归则通过函数L将w‘x+b对应一个概率p,p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。
已知输入一个n维特征向量x(可能是一张图),需要识别出这是不是一张猫图。你希望得出一个概率y^(处于0、1之间)。logistic回归参数w也是n维的,b是一个实数,所以已知输入x和参数w、b,根据y =w‘x+b计算出的结果范围并不在0、1之间,所以我们要对结果做进一步sigmoid处理,这样就使得结果处于0、1之间。sigmoid函数值∈(0,1)。
即:y^=sigmoid(wTx+b)
因为w,x均为向量,所以wTx结果为一个数,从而逻辑回归计算结果为一个数。
2.2.损失函数(Loss Function)
现在为了训练逻辑回归函数里的参数w和b,我们需要一个成本函数(cost function)。
我们通过损失函数/误差函数(Loss(error) function)来衡量预测输出值y^和y的实际值有多接近。
损失函数是在单个训练样本中定义的,它衡量了在单个训练样本上的表现。
成本函数衡量的是全体样本的表现,即衡量参数w和b的效果。
损失函数L越小,代表y^和y越接近,下图将成本函数J设置为各个样本损失函数值的平均值,因此成本函数越小,代表y^和y越接近。
2.3.梯度下降法(Gradient Descent)
逻辑回归的成本函数如下,我们想要找到使成本函数最小的参数w,b。首先我们要用某初始值初始化w和b,对于逻辑回归几乎所有初始值均可,由于成本函数是凸函数,所以无论从哪里开始初始化,成本函数都会下降到同一点或附近。
梯度下降法所做的就是从初始点开始朝最陡的下坡方向走一步(梯度是方向导数最大的方向,即最陡的方向),在梯度下降一步后,或许在那里停下,因为它整视图朝最快下降的方向往下走,这是梯度下降的一次迭代,通过数次迭代或许会到达最底端。
为了更好理解梯度下降,现先忽略b轴,我们将重复执行以下的更新操作:
其中α为学习率(learning rate),如下图所示,如果w初始在底端右侧,导数为正,w逐渐向左移动。同样的,如果w在左边,导数为负,w逐渐向右移动。所以不管w在何处,最终都能逐渐收敛到最底端。
同样的,放到二元函数J(w,b)中,参数w和b是交替梯度下降的:
2.4.计算流程图(Computation Graph)
可以说,一个神经网络的计算都是按照前向或反向传播过程来实现的,首先计算出神经网络的输出,紧接着进行一个反向传输操作,后者我们用来计算出对应的梯度或者导数。
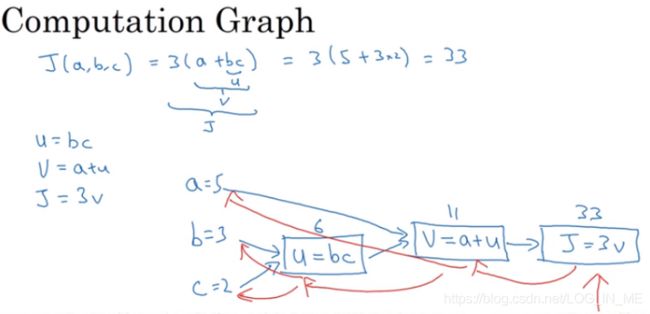 到我们利用反向传播计算结果J对各个变量的导数的时候,我们是这样计算导数的:
到我们利用反向传播计算结果J对各个变量的导数的时候,我们是这样计算导数的:
以第一个反向红箭头为例,取v为一个值,得J的值;然后改变v的值,J也相应改变,然后计算J的变量与v变化的量的倍数,即dJ/dv。剩下的变量的导数可以计算中间变量的导数并利用链式求导法则逐步计算出来。
2.5.逻辑回归中的梯度下降法(Logistic Regression Gradient descent)
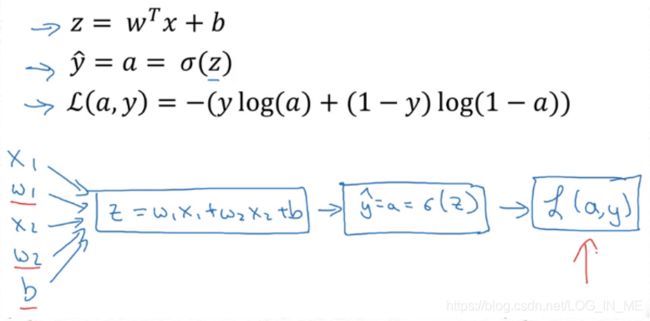 对于逻辑回归的计算流程图如上所示(假设该样本x=(x1,x2),w=(w1,w2),b=b),我们需要通过反向传导计算出最终的L对各参数的导数,来不断更新w1、w2、b的值,最终收敛至损失函数的最底端。
对于逻辑回归的计算流程图如上所示(假设该样本x=(x1,x2),w=(w1,w2),b=b),我们需要通过反向传导计算出最终的L对各参数的导数,来不断更新w1、w2、b的值,最终收敛至损失函数的最底端。
 现将单个样本扩大到m个样本,全局的成本函数对各参数的导数=m个样本的损失函数对参数的导数。所以利用梯度下降法最后更新参数时,是根据全局的成本函数对各参数的导数进行计算的。
现将单个样本扩大到m个样本,全局的成本函数对各参数的导数=m个样本的损失函数对参数的导数。所以利用梯度下降法最后更新参数时,是根据全局的成本函数对各参数的导数进行计算的。
2.6.向量化逻辑回归(Vectorizing Logistic Regression)
在深度学习等领域,面对大数据集,如果显示地使用for循环遍历样本,将会花费大量的时间,效率很低,所以需要将数据向量化以实现同时处理整个训练集,来实现梯度下降法的一步迭代。
2.7.逻辑回归损失函数的解释(Explanation of logistic regression cost function)
y^为在现有样本训练下的y=1的概率,则现有样本训练条件下的y=0的概率为1-y^。综合起来,p(y|x)如下图红框所示的0-1概率分布,进一步将p(y|x) log起来,由于p(y|x)介于0-1之间,所以logp(y|x)为负。此时logp(y|x)为损失函数的相反数,由于y^越接近y,损失函数越小,所以前面要添个负号。
接下来我们将上述各个样本的logp求平均值即为成本函数,我们利用最大似然估计(最大似然估计即求出一组参数,使这个式子取得最大值)求出使该式最小的一组参数(负号里面为最大值)。
3.浅层神经网络(One hidden layer Neural Network)
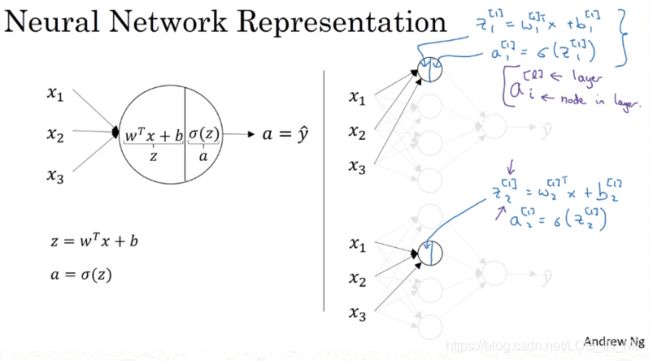
3.1.神经网络表示(Neural Network Representation)
如上图所示:
- 从左到右分别为输入层(第0层,产生的值用a[0]表示)、隐藏层(第1层,产生的值用a[1]表示)、输出层(第2层,产生的值用a[2]表示)。上标[i]表示第i层产生的值。
- 第2层几个神经元产生的值可以分别用a[2]_1、a[2]_2……表示。(上图右下角所示)
- 输入层(第0层)不算一层,所以上图神经网络为双层神经网络。
- 由于神经网络的训练只需要给输入层和输出层的数据,中间的层计算过程是看不到的,所以叫做隐藏层。
3.2.计算神经网络的输出(Computing a Neural Network's Output)
每个神经元的内部构造如上图所示,向量化的计算方法如下图所示。
上图第1层的w[1]和b[1]的维度分别是3x1、4x1,下图第2层输出层w[2]和b[2]的维度分别为4x1(未转置)、1x1。在实际编程过程中,只需要计算下述四个式子即可完成该神经网络的计算。
上述只是单个样本的计算,扩大到m个样本的训练,即将向量扩大为矩阵,这样第1层计算出来的结果矩阵A(如下图右下角所示)列标代表了样本序号,行标代表了隐藏神经元的序号。
3.3.激活函数(Activation functions)
在构建一个神经网络时,可以选择的是在隐藏层和输出层中用哪一个激活函数。之前我们一直使用的是sigmoid函数,在实际过程中我们可以选择其他不同的激活函数(可以是非线性的函数)。
【tanh函数】双曲正切函数,其效果几乎比sigmoid函数还要好。介于-1、1之间。
tanh函数在几乎任何场合效果逗比sigmoid函数好,但是对于二分分类的输出层,由于要求预测值在0-1之间,需要使用sigmoid函数。所以可以隐藏层用tanh函数,输出层用sigmoid函数。
tanh函数和sigmoid函数都有一个缺点:当z很大或很小时,函数的斜率非常小,接近于0,这样会拖慢梯度下降的速度。
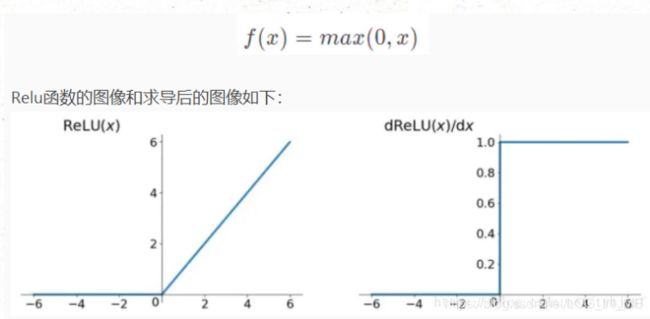
【ReLU函数】修正线性单元,遇事不决,ReLU函数。
ReLU函数有个缺点:当自变量为负时,斜率为0。
对此有个带泄漏的ReLU函数(Leaky ReLU),在自变量z小于0时,a=0.01z,是个较缓的斜坡。(如下图右下角所示)
3.4.神经网络中的梯度下降算法(Gradient descent for Neural Networks)
首先随机初始化参数值,然后进行正向传播,根据正向传播的数据计算成本函数J对各参数的导数,以此更新各参数值。循环往复直到参数收敛。
3.5.随机初始化(Random Initialization)
如果将神经网络的各参数数组全部初始化为0,再使用梯度下降算法,那会完全无效。因为如此以来,每个神经元的函数就会完全一样,在做完全一样的计算,通过多次迭代之后依然在计算完全一样的函数没有进展。
只要w随机初始化,b可以全为0。因为只要w不同,每个隐藏神经元计算的函数就不同。
通常我们把权重矩阵w初始化为很小的随机值,因为如果使用sigmoid函数或tanh函数,如果权重w太大,在计算激活函数值时,g(z)的z会变得很大或很小,这样激活函数的斜率会变得很小,意味梯度下降法会变得很慢,学习的很慢。一般会在随机初始化的random()函数前乘以0.01。
4.深层神经网络(Deep Neural Networks)
4.1.深层神经网络(Deep Neural Networks)
4.2.为什么要用深层表示?(Why deep representations?)
其实不一定要有多大的隐藏层,但是深度得够深。
深度神经网络究竟在计算什么?
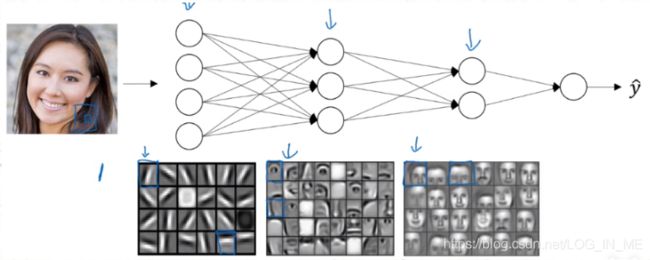
当在人脸识别的时候,深度神经网络所做的事情就是:当你输入一张脸部的照片,然后你可以把深度神经网络的第一层当成一个特征探测器或者边缘检测器(例如下图中第1层每个小格子对应一个隐藏单元),第一层用来找图片中的各种边缘。
我们可以把照片里组成边缘的像素们放在一起看,然后它可以把被检测的边缘组合成面的不同部分,例如一个神经元可能在找眼镜的部分,另一个神经元在找鼻子的部分。然后把这许多的边缘结合在一起,就可以开始检测人脸的不同部分。
最后再把这些部分(比如眼睛鼻子下巴)放在一起,就可以识别人脸了。
通常边缘探测器会检测图片很小的一部分,而面部检测器会检测更大的部分。像这样先检测低层特征,然后由小部分组成整体,由简单到复杂的思想可以运用到深度学习的其他应用上。通常前面的层用来识别简单的低层特征,到后面的层就能做更多复杂的事情了。如对音频进行检测时,可以先收集较低的波形特征,再将这些波形组合在一起,先识别一个个声音单元,再组合成整体的单词。
另一个说明深层网络为什么有效的理论来源于电路理论:如果用浅层的神经网络来计算同样的函数,也就是不用很多的隐藏层时,你会需要指数增长的单元数量才能达到同样的效果。
4.3.前向和反向传播(Forward and backword functions)
如上图所示,神经网络的每一层都有一个正向传播和反向传播的过程,正向传播通过该层的输入a[l-1]和该层的参数w[l]、b[i]计算出a[l],并将中间结果z[l]缓存。再进行一次反向传播,利用微分(增量)da[l]和dz[l]
4.4.参数及超参数(Parameters vs Hyperparameters)
要想深度神经网络起到很好的效果,规划好参数及超参数很重要。
以逻辑回归为例:
参数:w,b
超参数:除了w,b以外要用到的参数,如学习率α、梯度下降循环的数量、隐层数……
因为这些参数的设置最终会影响到w和b,所以叫做超参数。
4.5.这和大脑有什么关系?(Why does this have to do with the brain?)
实际上关联不大。
将神经元的工作方式等类比于深度学习的工作方式其实是过度简化了神经元的工作方式,因为这种形容很简洁,也很容易让人普遍接受。实际上神经元的具体工作方式就连生物科学家也没有研究清楚。