pytorch backward使用解析

前言

torch版本为v1.13。

backward函数官方文档

torch.Tensor.backward：计算当前tensor相对于图的叶子的梯度。

叶子可以理解为自己创建的变量。使用链式法则，图是可微的。如果张量不是标量，并且需要梯度，该函数还需要指定gradient。它应该是匹配类型和位置的tensor，包含微分函数相对于self的梯度(???)。

这个函数在叶子中累计梯度，在调用它之前，可能需要将.grad属性归零或将它们设置为 None 。

参数：

• gradient (Tensor or None) – 关于tensor的梯度。如果它是一个tensor，会自动转为不需要grad的Tensor，除非create_graph为True。None值可以指定为标量Tensor或不需要grad的Tensor。如果None值是可接受的，那么该参数是可选参数。
• retain_graph (bool, optional) – 如果为False，用于计算grads的graph将被释放。注意，在几乎所有情况下，都不需要将此选项设置为 True，而且通常可以以更有效的方式解决。 默认为 create_graph 的值。
• create_graph (bool, optional) – 默认为False。如果为True，导数的图将会被构建，允许计算更高阶的导数衍生品（derivative products）。
• inputs (sequence of Tensor) – 将梯度累积到inputs 的 .grad 中。其他的Tensors将会被忽略。如果未提供，则梯度将累积到用于计算 attr::tensors 的所有叶张量中。

backward理解

Jacobian矩阵

参考：wolfram-Jacobian
设 $\mathbf{x}=(x_1,x_2,\cdots ,x_n{)}^T$，$\mathbf{y}=f(\mathbf{x})$，则有：
y = [ y 1 y 2 ⋮ y m ] = [ f 1 ( x ) f 2 ( x ) ⋮ f m ( x ) ] = [ f 1 ( x 1 , x 2 , ⋯   , x n ) f 2 ( x 1 , x 2 , ⋯   , x n ) ⋮ f m ( x 1 , x 2 , ⋯   , x n ) ] \bold{y}= \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \\ \end{bmatrix}= \begin{bmatrix} f_1(\bold{x}) \\ f_2(\bold{x}) \\ \vdots \\ f_m(\bold{x}) \\ \end{bmatrix}= \begin{bmatrix} f_1(x_1,x_2,\cdots,x_n) \\ f_2(x_1,x_2,\cdots,x_n) \\ \vdots \\ f_m(x_1,x_2,\cdots,x_n) \\ \end{bmatrix} y= ​y1​y2​⋮ym​​ ​= ​f1​(x)f2​(x)⋮fm​(x)​ ​= ​f1​(x1​,x2​,⋯,xn​)f2​(x1​,x2​,⋯,xn​)⋮fm​(x1​,x2​,⋯,xn​)​ ​，则 $\mathbf{y}$ 关于 $\mathbf{x}$ 的梯度是一个雅可比矩阵：
J ( x 1 , x 2 , ⋯   , x n ) = ∂ ( y 1 , ⋯   , y m ) ∂ ( x 1 , ⋯   , x n ) = [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ⋯ ∂ y 1 ∂ x n ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ⋯ ∂ y 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ y m ∂ x 1 ∂ y m ∂ x 2 ⋯ ∂ y m ∂ x n ] J(x_1,x_2,\cdots,x_n) = {\frac {\partial(y_1,\cdots,y_m)} {\partial(x_1,\cdots,x_n)}}= \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} & \cdots &\frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}}& \frac{\partial y_{2}}{\partial x_{2}} & \cdots & \frac{\partial y_{2}}{\partial x_{n}}\\ \vdots &\vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}}& \frac{\partial y_{m}}{\partial x_{2}} &\cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{bmatrix} J(x1​,x2​,⋯,xn​)=∂(x1​,⋯,xn​)∂(y1​,⋯,ym​)​= ​∂x1​∂y1​​∂x1​∂y2​​⋮∂x1​∂ym​​​∂x2​∂y1​​∂x2​∂y2​​⋮∂x2​∂ym​​​⋯⋯⋱⋯​∂xn​∂y1​​∂xn​∂y2​​⋮∂xn​∂ym​​​ ​

vector-Jacobian product的计算

参考：
The “gradient” argument in Pytorch’s “backward” function
详解Pytorch 自动微分里的(vector-Jacobian product)-知乎

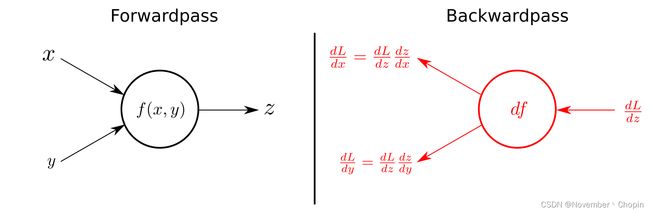
backward（torch.autograd.backward或Tensor.backward）实现的是vector-Jacobian product，即矢量-雅可比积，Jacobian容易理解，这里的vector（设为$v$）就是backward的gradient参数，有很多种理解：

• $y_i$ 对 $x_i$ 的偏导数沿$v$上的投影，$v$的默认方向为 $v=(1,1,\cdots ,1)$；
• 各个分量函数关于$x_i$偏好的权重

值得注意的是，$v$ 的维度与输出保持一致，可正可负。

所以，vector-Jacobian product的形式为：
v ⋅ J = [ v 1 , v 2 , ⋯   , v m ] ⋅ [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ⋯ ∂ y 1 ∂ x n ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ⋯ ∂ y 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ y m ∂ x 1 ∂ y m ∂ x 2 ⋯ ∂ y m ∂ x n ] = [ ∑ i = 0 m ∂ y i ∂ x 1 v i ,     ∑ i = 0 m ∂ y i ∂ x 2 v i ,     ⋯   ,     ∑ i = 0 m ∂ y i ∂ x n v i ] \begin{aligned} \bold{v} \cdot J &= [v_1,v_2,\cdots,v_m]\cdot \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} & \cdots &\frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}}& \frac{\partial y_{2}}{\partial x_{2}} & \cdots & \frac{\partial y_{2}}{\partial x_{n}}\\ \vdots &\vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}}& \frac{\partial y_{m}}{\partial x_{2}} &\cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{bmatrix}\\ &= \begin{bmatrix} \sum_{i=0}^{m}{\frac {\partial y_i} {\partial x_1}v_i},\,\,\, \sum_{i=0}^{m}{\frac {\partial y_i} {\partial x_2}v_i},\,\,\, \cdots,\,\,\, \sum_{i=0}^{m}{\frac {\partial y_i} {\partial x_n}v_i} \end{bmatrix} \end{aligned} v⋅J​=[v1​,v2​,⋯,vm​]⋅ ​∂x1​∂y1​​∂x1​∂y2​​⋮∂x1​∂ym​​​∂x2​∂y1​​∂x2​∂y2​​⋮∂x2​∂ym​​​⋯⋯⋱⋯​∂xn​∂y1​​∂xn​∂y2​​⋮∂xn​∂ym​​​ ​=[∑i=0m​∂x1​∂yi​​vi​,∑i=0m​∂x2​∂yi​​vi​,⋯,∑i=0m​∂xn​∂yi​​vi​​]​

这就是输出进行backward之后，叶子张量的.grad值。

vector-Jacobian product的例子理解

以$y=x^2$为例进行解释：
代码1：

x = torch.tensor([1,2,3.], requires_grad=True)
y = x**2
y.backward(gradient=torch.tensor([1,1,1.]))
print(x.grad)
"""
输出:
tensor([2., 4., 6.])
"""

代码2：

x = torch.tensor([1,2,3.], requires_grad=True)
y = x**2
y.backward(gradient=torch.tensor([10,-10,20.]))
print(x.grad)
"""
输出:
tensor([ 20., -40., 120.])
"""

可以发现，代码2相比于代码1，结果放大了gradient倍。设上述代码中的$\mathbf{x}=(x_1,x_2,x_3)$，则$\mathbf{y}=(y_1,y_2,y_3)=(x_1^2,x_2^2,x_3^2)$，gradient为$\mathbf{v}=(v_1,v_2,v_3)$。使用vector-Jacobian product公式可得：

v ⋅ J = [ v 1 , v 2 , v 3 ] [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 1 ∂ x n ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ∂ y 2 ∂ x n ∂ y 3 ∂ x 1 ∂ y 3 ∂ x 2 ∂ y 3 ∂ x n ] = [ ∑ i = 0 3 ∂ y i ∂ x 1 v i ,     ∑ i = 0 3 ∂ y i ∂ x 2 v i ,     ∑ i = 0 3 ∂ y i ∂ x 3 v i ] = [ 2 x 1 v 1 , 2 x 2 v 2 , 2 x 3 v 3 ] = [ 2 v 1 , 4 v 2 , 6 v 3 ] \begin{aligned} \bold{v} \cdot J &= [v_1,v_2,v_3] \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} &\frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}}& \frac{\partial y_{2}}{\partial x_{2}} & \frac{\partial y_{2}}{\partial x_{n}}\\ \frac{\partial y_{3}}{\partial x_{1}}& \frac{\partial y_{3}}{\partial x_{2}} & \frac{\partial y_{3}}{\partial x_{n}} \end{bmatrix}\\ &= \begin{bmatrix} \sum_{i=0}^{3}{\frac {\partial y_i} {\partial x_1}v_i},\,\,\, \sum_{i=0}^{3}{\frac {\partial y_i} {\partial x_2}v_i},\,\,\, \sum_{i=0}^{3}{\frac {\partial y_i} {\partial x_3}v_i} \end{bmatrix} \\ &=\begin{bmatrix}2x_1v_1,2x_2v_2,2x_3v_3\end{bmatrix} \\ &=\begin{bmatrix}2v_1,4v_2,6v_3\end{bmatrix} \end{aligned} v⋅J​=[v1​,v2​,v3​] ​∂x1​∂y1​​∂x1​∂y2​​∂x1​∂y3​​​∂x2​∂y1​​∂x2​∂y2​​∂x2​∂y3​​​∂xn​∂y1​​∂xn​∂y2​​∂xn​∂y3​​​ ​=[∑i=03​∂x1​∂yi​​vi​,∑i=03​∂x2​∂yi​​vi​,∑i=03​∂x3​∂yi​​vi​​]=[2x1​v1​,2x2​v2​,2x3​v3​​]=[2v1​,4v2​,6v3​​]​

分别将 $\mathbf{v}=(1,1,1.)$ 和 $\mathbf{v}=(10,-10,20.)$ 带入可得代码结果。

输入和输出为标量或向量时的计算

输入为标量，输出为标量

代码：

x = torch.tensor(2., requires_grad=True)
y = x**2+x
y.backward(gradient=torch.tensor(1.))
print(x.grad)
"""
输出:
tensor([5.])
"""

解释：
$\mathbf{x}=x_1$，则$\mathbf{y}=y_1=x_1^2+x_1$，gradient为$\mathbf{v}=v_1$，则：
$$\begin{array}{rl}\mathbf{v}\cdot J& =[v_1]\cdot [\frac{\partial y_1}{\partial x_1}]\\ & =[v_1]\cdot [2x_1+1]\\ & =[1]\cdot [2\times 2+1]\\ & =5\end{array}$$

输入为标量，输出为向量

代码：

x = torch.tensor(1., requires_grad=True)
y = torch.empty(2)
y[0] = x**2
y[1] = x**3
y.backward(gradient=torch.tensor([1,2.]))
print(x.grad)
"""
输出:
tensor(8.)
"""

解释：
$\mathbf{x}=x_1$，则$\mathbf{y}=[y_1,y_2]=[x_1^2,x_1^3]$，gradient为$\mathbf{v}=[v_1,v_2]$，则：
$$\begin{array}{rl}\mathbf{v}\cdot J& =[v_1,v_2]\cdot \left[\begin{array}{c}\frac{\partial y_1}{\partial x_1}\\ \frac{\partial y_2}{\partial x_1}\end{array}\right]\\ & =[v_1,v_2]\cdot \left[\begin{array}{c}2x_1\\ 3x_1^2\end{array}\right]\\ & =[1,2]\cdot \left[\begin{array}{c}2\\ 3\end{array}\right]\\ & =8\end{array}$$

输入为向量，输出为标量

代码：

x = torch.tensor([1.,2,3], requires_grad=True)
y = torch.sum(x**2)
y.backward()
print(x.grad)
"""
输出:
tensor([2., 4., 6.])
"""

解释：
$\mathbf{x}=[x_1,x_2,x_3]$，则$\mathbf{y}=y_1=x_1^2+x_2^2+x_3^2$，gradient为$\mathbf{v}=[v_1]$，则：
$$\begin{array}{rl}\mathbf{v}\cdot J& =[v_1]\cdot \left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \frac{\partial y_1}{\partial x_3}\end{array}\right]\\ & =[v_1]\cdot \left[\begin{array}{ccc}2x_1& 2x_2& 2x_3\end{array}\right]\\ & =[1]\cdot \left[\begin{array}{ccc}2& 4& 6\end{array}\right]\\ & =\left[\begin{array}{ccc}2& 4& 6\end{array}\right]\end{array}$$

输入为标量，输出为向量

参见上一节 vector-Jacobian product的例子理解。

额外例子：输出为标量，gradient为向量

在上一节的例子中，gradient的维度与输出维度保持一致，本节探索gradient的维度与输出维度不一致的情况。

输入为标量，输出为标量，gradient为向量

x = torch.tensor(2., requires_grad=True)
y = x**2+x
y.backward(gradient=torch.tensor([1.,10]))
print(x.grad)

结果：报错

RuntimeError: Mismatch in shape: grad_output[0] has a shape of torch.Size([4]) and output[0] has a shape of torch.Size([]).

输入为向量，输出为标量，gradient为向量

x = torch.tensor([1.,2,3], requires_grad=True)
y = torch.sum(x**2)
y.backward(gradient=torch.tensor([1,2.]))
print(x.grad)

结果：报错

RuntimeError: Mismatch in shape: grad_output[0] has a shape of torch.Size([2]) and output[0] has a shape of torch.Size([]).

总结

• gradient默认为1，其维度应与输出维度保持一致；
• gradient类似于在梯度前面乘以一个动量，类似于学习率，不过可正可负（个人理解）；

$■$