使用卡尔曼滤波器进行回声消除

回声消除的基本原理就是基于自适应滤波器来消除回声，而目前流行的方法基本上都是基于NLMS自适应滤波器算法优化而来，有收敛速度慢、回声消除能力不强、无法快速跟踪回声路径变化等问题。而基于卡尔曼滤波的回声消除，在各方面则要比NLMS算法强得多，能够极大提升回声消除的效果。因此这篇文章简单介绍下怎样使用卡尔曼滤波来进行回声消除。

lms filter

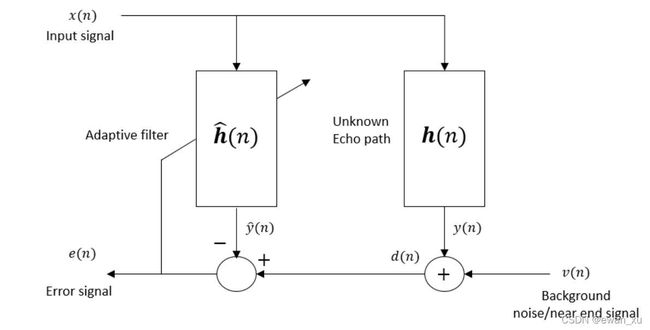
回声消除的原理就是通过远端参考信号与进行卷积得到估计的回声信号​，然后从近端麦克风信号中减去回声信号​得到回声消除后的信号，lms自适应滤波器就是通过随机梯度下降最小化误差信号的均方误差，来估计声学回声路径逼近真实回声路径

lms滤波器算法步骤如下：
假设真实的回声路径长度为

在n时刻输入的远端参考信号为：

估计的回声为：

估计的回声和近端信号间的误差为：

系数更新公式：

kalman filter

背景

卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。
简单来说就是系统利用前一时刻的状态，当前的输入值和可能的测量值来得到当前时刻下的状态的最优估计，因此卡尔曼滤波器和自适应滤波器一样都是递归算法。
他的广泛应用已经超过30年，包括机器人导航，控制，传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等等。近来更被应用于计算机图像处理，例如头脸识别，图像分割，图像边缘检测等等。

由于关于怎样使用卡尔曼滤波器做回声消除已经有前辈做出来了，所以为了可以更加容易的理解卡尔曼滤波器，只是应用形象的描述方法来讲解，然后简单介绍卡尔曼滤波器公式，推导就省略了。

最简单的例子

考虑你正在驾驶一辆直线行驶的小车，你通过油门深浅控制小车前进，车上有速度计可以测量你的车目前的速度，但是由于精度，传感器误差等影响，测量值并不精确，所以你需要解决的问题是：如何精确测量小车在某个时刻的真实速度。

我们定义：
是n时刻系统的输入，即小车的油门
​是n时刻系统的测量值，即小车的速度计的速度
是n时刻系统的状态，即小车的真实速度
我们将小车看作一个系统，示意图如下：

定义​是n时刻估计的系统的状态，那我们的目标就是精确估计​，让​和​之间的误差最小
首先建立输入与状态之间的模型，假设跟当前的油门输入和上一个时刻我们计算得到的小车速度​有关：

表示上个状态与当前状态的关系，表示当前输入与当前状态的关系，就是我们估计得到的n时刻小车速度，但很不幸，真实的场景下的小车速度肯定会受到比如风速、摩擦力等影响导致真实速度与估计速度出现偏差，所以我们的模型加上了噪声项​，称为过程噪声。
因为我们无法对噪声进行精确建模，所以我们的估计值是不考虑噪声的影响的：

这里是我们通过上一个状态以及模型估算出来的当前状态，我们叫它先验状态估计
很明显这个状态是不精确的，我们还需要利用到测量值，我们建立状态与测量值之间的模型，然后利用当前状态估计测量值，这样我们就能通过测量值知道我们的状态是否估计准确：

表示当前状态与当前测量值之间的关系，在这个例子测量值和状态都是小车的速度，所以这里表示测量速度和估计速度间的转换关系，但因为测量值也会有误差，所以我们的测量模型也加上了噪声项​，称为测量噪声。
通过这个模型，我们又有另一种方式去计算小车状态了：

好了，现在用了两种方式来估计小车状态，分别是​和​​，因为这两种方式估计都有误差，所以我们可以结合这两种方式来精确估计小车状态，那么卡尔曼滤波器就可以派上用场了，它结合这两条信息给出最优的状态估计，示意图如下：

接下来我们就可以对卡尔曼滤波器原理做一个概述了：
卡尔曼滤波器基于以下假设，然后不断的利用上一个状态迭代估计当前状态：
1、状态转移模型，控制模型和观测模型是线性的
2、过程噪声和观测噪声假设为零均值高斯噪声

我们怎么对两个状态的估计结果相结合呢，很自然的可以想到对两者的结果进行加权：

当K=0时，
当K=1时，

所以卡尔曼滤波器的目标就是寻找K，使和之间的误差最小，定义状态的误差为：

将误差也看做高斯分布，对应的协方差矩阵为：

为了使估计的状态最优，目标是最小化后验状态误差的协方差

推导步骤就省略不写了，对于我们使用卡尔曼滤波器的话只需要知道其思想原理以及怎么使用就可以了，最终我们得到卡尔曼滤波器的公式如下：

时间更新方程：
1、
2、
状态更新方程：
3、
4、
5、​

其中：
：是n时刻的先验状态估计值
​：n-1时刻的后验状态估计值
：n-1时刻状态到n时刻状态的转移矩阵
：n时刻的输入
：输入转换为状态的矩阵
：n时刻先验状态估计的误差协方差
：n-1时刻后验状态估计的误差协方差
：系统的过程噪声的协方差
：卡尔曼增益
：状态到测量的转换矩阵
：测量噪声​的的协方差
​：n时刻的后验状态估计值
​：观测值
​：n时刻后验状态估计的误差协方差
：单位矩阵

使用卡尔曼滤波器回声消除

很显然，在回声消除系统中，回声路径就是我们需要估计的系统状态，因此我们可以利用卡尔曼滤波器来对回声路径进行估计。
我们令n时刻参考信号为，近端录制信号为，n时刻的误差输出为，n时刻卡尔曼滤波器的状态为
一般我们认为回声路径是一个稳定的非常缓慢变化的过程，遵循一阶马尔可夫模型。因此，对比卡尔曼滤波器的状态更新方程，其中为单位矩阵，没有对回声路径的控制项，所以​可以忽略，这样状态更新方程可以定义为：

其中就是卡尔曼滤波器测量误差，即：

我们得到到卡尔曼滤波器回声消除的更新公式如下：

要使用卡尔曼滤波回声消除还需要估计两个噪声协方差矩阵 和，一般说来也都是根据输入输出参数以及滤波器参数来进行估计，这里就不展开讲了

总结

lms自适应滤波器是通过最小化近端信号与误差信号的均方误差，通过随机梯度下降来达到估计回声路径的目的，所以当近端有双讲时，会使滤波器迅速发散，步长设置小，误差较小，但收敛慢，步长设置大 ，收敛快，但误差大。
而kalman滤波器的目标是最小化状态误差的协方差，可以分析，在双讲时，意味着测量误差很大，这时候K就很小，状态的估计值更倾向于估计出来的结果，即滤波器系数不更新，因此双讲时滤波器不易发散，当测量误差小时，K很大，状态的估计值更倾向于测量值，所以很快就可以收敛。所以同时兼顾了快速跟踪以及双讲，要比基于lms的自适应滤波器的效果好很多

效果对比

在这里我对比3个自适应滤波器的回声消除效果，AEC3的自适应滤波器、滴滴开源的子带ipnlms滤波器、以及我自己实现的卡尔曼滤波器

1、线性回声的语料：

远端信号	近端信号

AEC3	滴滴	卡尔曼滤波

 2、在iphone上录制的真实语料：

远端信号	近端信号

AEC3	滴滴	卡尔曼滤波

在回声是线性的情况下，AEC3自适应滤波器约能消除15dB回声 ，滴滴IPNLMS约能消除21dB回声， 而卡尔曼滤波可以消除高达45dB，基本可以完全消除线性回声

在iphone真实录制的语料下，回声有非线性失真，因此相比线性回声，回声消除能力都有所下降，AEC3自适应滤波器仅能消除约4dB回声，滴滴IPNLMS约能消除8dB回声，而卡尔曼滤波还能消除高达21dB回声

 上述自适应滤波器对比测试语料放在：https://github.com/ewan-xu/AecSamples

kalman滤波器简单实现

在这里贴上使用python实现一个简单的时域卡尔曼自适应滤波，代码如下：

import numpy as np
import librosa

def kalman_filter(x, d, M = 64):
    length = min(len(x),len(d))
    beta = 0.9
    R = 1e-2
    Q = 1e-5
    H = np.zeros(M)
    P = np.full(M,Q)
    y = np.zeros(length-M)
    e = np.zeros(length-M)
    
    for n in range(length-M):
        x_n = x[n:n+M][::-1]
        d_n = d[n] 
        y_n = np.dot(H, x_n.T)
        e_n = d_n - y_n
        R = beta*R + (1-beta)*(e_n**2)
        Pn = P + Q
        K = Pn*x_n.T/(x_n*Pn*x_n.T + R)
        H = H + K*e_n
        P = (1.0 - K*x_n.T)*Pn
        y[n] = y_n
        e[n] = e_n
    return y, e
    
if __name__ == "__main__":
    x = librosa.core.load('ref.wav',sr=8000,mono=True)[0]
    d = librosa.core.load('rec.wav',sr=8000,mono=True)[0]

    M = 64
    y, e = kalman_filter(x,d,M)

    librosa.output.write_wav('estimate.wav',y,sr=8000)
    librosa.output.write_wav('error.wav',e,sr=8000)

还有基于频域的卡尔曼滤波，以及其他的自适应滤波器，感兴趣的同学可以去我的repository中查看： https://github.com/ewan-xu/pyaec

有任何疑问，欢迎加微信交流：xu19315519614