线性卷积、循环卷积与FFT之间的关系

线性卷积与循环卷积

在音频信号处理中，卷积是很常见的信号处理方式，例如fir滤波器，卷积的计算公式也非常简单，对于系统h和输入信号x，卷积的计算公式如下：

$y(t)=\sum _{m=0}^{N-1}x(t-m)h(m)$

这种普通的卷积也称为线性卷积，一个长为L的信号x和长为M的系统h进行卷积，相当于在x的前后做M-1个点的padding，然后再与h进行卷积运算，结果的长度为L+M+1

$y(t)=[\sum _{m=0}^{N-1}x(t-m)h(m)]R_N(t)$
而一个N点循环卷积相当于将x和h做周期为N的延拓后进行卷积，然后再取其主值区间，得到的结果长度为N
我们定义$x=[1,2,3,4]$和$h=[5,6,7,8]$，下面用一张示意图来表示线性卷积和圆周卷积的计算方式：

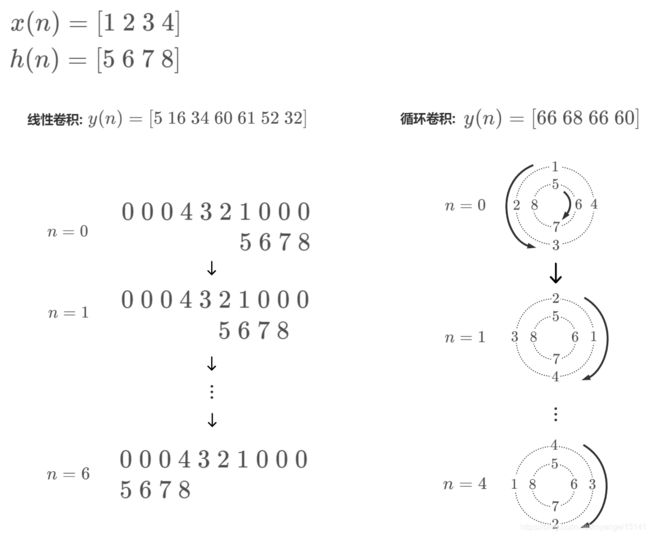
总结下来就是：
线性卷积：将x补零，反褶，然后滑动，与对应位置的h相乘求和
循环卷积：将x和h补零至N点，x逆时针平均分布在大圆上，h顺时针分布在小圆上，然后顺时针旋转大圆，与对应位置的h相乘求和
我们可以将卷积中每一步的滑动变换为矩阵乘法并行的进行卷积运算，对于循环卷积，将其变换为矩阵后是一个循环矩阵，我们利用python代码来求线性卷积和循环卷积：

import numpy as np
from scipy.linalg import toeplitz

def circular_convolve(x,h,N):
    c = np.pad(x,[0,N-len(x)],mode='constant')
    r = np.roll(c[::-1],1)
    x_c = toeplitz(c,r)
    h_c = np.pad(h,[0,N-len(h)],mode='constant')
    return np.dot(x_c,h_c)
    
def convolve(x,h):
    L = len(x)
    M = len(h)
    N = L+M-1
    x_p = np.pad(x,[M-1,M-1],mode='constant')
    index = np.arange(M)[::-1][None, :] + np.arange(N)[:, None]
    return np.dot(x_p[index],h)

x = [5,6,7,8]
h = [1,2,3,4]
L=4

print('线性卷积结果为:')
print(convolve(x,h))
print('循环卷积结果为:')
print(circular_convolve(x,h,L))

输出为：

线性卷积结果为:
[ 5 16 34 60 61 52 32]
循环卷积结果为:
[66 68 66 60]

卷积与FFT

虽然卷积的计算方法很简单，但是当x和h都很长的时候，卷积计算是非常耗费时间的。直接卷积运算的复杂度为$\mathcal{O}[N^2]$，因此有必要找到比直接计算卷积更快的办法。
相信大家都知道时域的卷积等于频域的乘积这个定理，因此要计算时域的卷积，可以将时域信号转换为频域信号，进行乘积运算之后再将结果转换为时域信号，实现快速卷积。
在我之前的文章使用python实现基-2FFT、基-4FFT快速傅里叶变换算法中分析到，经过优化的FFT其运算的复杂度为$\mathcal{O}[NlogN]$，显然通过FFT计算卷积要比直接计算快速得多。
不过由于FFT运算假设其所计算的信号为周期信号，因此通过FFT计算出的结果实际上是两个信号的循环卷积，而不是线性卷积。
使用numpy的fft来计算卷积：

import numpy as np

x = [5,6,7,8]
h = [1,2,3,4]

X = np.fft.rfft(x)
H = np.fft.rfft(h)
y = np.fft.irfft(X*H)

print('fft计算卷积结果为:')
print(y)

输出为：

fft计算卷积结果为:
[66. 68. 66. 60.]

可以看到，将x和h变换到频域相乘，然后变换回时域的结果与循环卷积的结果一致。
如果需要使用FFT计算线性卷积，就需要对信号进行补零扩展，使得其长度长于线性卷积结果的长度。
对x和h进行补零，然后再进行fft：

import numpy as np

x = [5,6,7,8]
h = [1,2,3,4]

X = np.fft.rfft(x,n=7)
H = np.fft.rfft(h,n=7)
y = np.fft.irfft(X*H,n=7)

print('fft计算卷积结果为:')
print(y)

输出为：

fft计算卷积结果为:
[ 5. 16. 34. 60. 61. 52. 32.]

可以看到，结果与线性卷积结果一致