python实现重叠保留法和重叠相加法分段计算卷积

概念

在音频信号处理中，卷积是很常见的信号处理方式，例如fir滤波器，卷积的计算公式也非常简单，对于输入信号$x(t)$和系统$h(t)$，卷积的计算公式如下：

$y(t)={\sum }_{m=0}^{M}x(t-m)h(m)$

很明显这种方式需要我们完全知道输入信号$x(t)$才能与$h(t)$计算卷积，实际应用中我们不可能预先获得整个信号，全部输入完之后才开始计算，因为这会造成输出有很大的延时，实际应用中我们往往都是按帧进行音频信号处理，例如每10ms一帧进行处理，然后实时返回处理后的信号，这时候我们就需要根据音频每帧信号，进行分段卷积。

分段卷积根据方式不同，有重叠相加法和重叠保留法两种，下面分别介绍两种方法

重叠相加法

重叠相加法基本思想是将长序列$x(t)$分为若干个子段$x_k(t)$，每个子段长为$L$,然后每个子段$x_k(t)$分别与长度为M的$h(t)$进行卷积得到每段的卷积结果$y_k(t)$，每段卷积的结果长度为$L+M-1$，其中后$M-1$为重叠部分，将重叠的部分相加一起合并起来便得到结果$y_k(t)$，示意图如下：

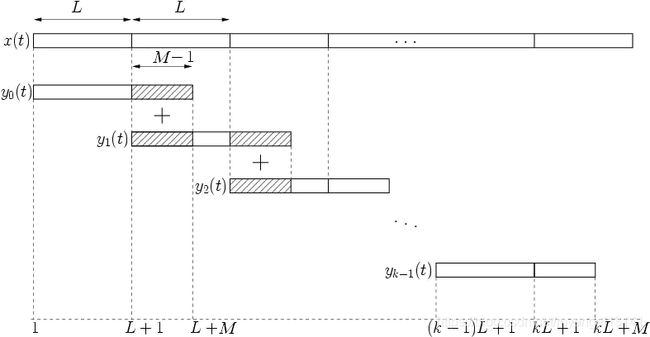
为了看的更清楚，我们举一个最简单的例子:
我们定义$x_k(t)=[0,1,2,3,4,5,6,7,8,9,10,11]$和$h(t)=[0,1,2,3]$
使用python计算卷积：

import numpy
x = np.arange(12)
h = np.arange(4)
y = np.convolve(x,h)

输出如下：

x: [ 0  1  2  3  4  5  6  7  8  9 10 11]
h: [0 1 2 3]
y: [ 0  0  1  4 10 16 22 28 34 40 46 52 58 52 33]

我们将x分为3段,每段长为4：

x0 = x[0:4]
x1 = x[4:8]
x2 = x[8:12]

每段$x_k(t)$如下：

x0: [0 1 2 3]
x1: [4 5 6 7]
x2: [ 8  9 10 11]

然后分别计算这3段的卷积：

y0 = np.convolve(x0,h)
y1 = np.convolve(x1,h)
y2 = np.convolve(x2,h)

每段卷积结果分别如下：

y0: [ 0  0  1  4 10 12  9]
y1: [ 0  4 13 28 34 32 21]
y2: [ 0  8 25 52 58 52 33]

由于h长度M=4,因此每段卷积结果的重叠长度为3，因此我们将重叠部分相加：

相加后的结果：

y': [ 0  0  1  4 10 16 22 28 34 40 46 52 58 52 33]

可以看到,跟整段卷积的结果是一样的。
那么我们可以推广到一般情况,计算分段长度为$L$，$h(t)$长度为$M$的重叠相加法的步骤可以总结如下：

1、初始化

• 创建重叠区缓存，大小为$N=L+M-1$，初始化为0

2、计算结果

• 对当前的$L$点分段数据$x_k(t)$与$h(t)$计算卷积,得到$L+M-1$个结果$y_k(t)$
• $y_k(t)$的前$L$个点与重叠区缓存前$L$个点相加，便是当前分段的卷积结果

3、缓冲区更新

• 缓冲区的后$M-1$个点与$y_k(t)$后$M-1$个点相加
• 缓冲区向前移动$L$个点
• 缓冲区后$L$个点置0

python代码如下：

def overlap_add_conv(x,h,L):
  M = len(h) # 滤波器长度
  N = L+M-1 # 每段卷积后长度
  nb = len(x)//L #块数量
  y = np.zeros((nb,L)) #卷积结果
  mem = np.zeros(N) # overlap缓存
  for n in range(nb):
    # 对x进行分段，每段长为L
    x_n = x[n*L:(n+1)*L]
    # 计算卷积
    y_n = np.convolve(x_n, h)
    # 计算前L个点结果
    y[n] = y_n[:L] + mem[:L]
    # overlap更新并向前移动L个点
    mem[L:] += y_n[L:]
    mem[:M-1] = mem[L:]
    mem[M-1:] = 0
  return y.ravel()

直接卷积运算的复杂度为$\mathcal{O}[N^2]$，我们可以使用FFT来加速卷积的运算，FFT的复杂度为$\mathcal{O}[NlogN]$。
关于FFT的介绍可以参考：使用python实现基-2FFT、基-4FFT快速傅里叶变换算法
关于如何使用FFT计算卷积以及在重叠保留法中如何计算循环卷积可以参考：线性卷积、循环卷积与FFT之间的关系
我们将以上代码修改为使用FFT计算卷积如下：

def overlap_add_conv(x,h,L):
  M = len(h) # 滤波器长度
  N = L+M-1 # 每段卷积后长度
  nb = len(x)//L #块数量
  y = np.zeros((nb,L)) #卷积结果
  mem = np.zeros(N) # overlap缓存
  H = np.fft.rfft(h,n=N)
  for n in range(nb):
    # 对x进行分段，每段长为L
    x_n = x[n*L:(n+1)*L]
    # 使用FFT计算卷积
    X_n = np.fft.rfft(x_n,n=N)
    y_n = np.fft.irfft(X_n*H,n=N)
    # 计算前L个点结果
    y[n] = y_n[:L] + mem[:L]
    # overlap更新并向前移动L个点
    mem[L:] += y_n[L:]
    mem[:M-1] = mem[L:]
    mem[M-1:] = 0
  return y.ravel()

重叠保留法

与重叠相加法的不同在于,重叠保留法是每次分段的输入块有重叠，而输出无重叠。首先也是将长序列$x(t)$分为若干个子段$x_k(t)$，每个子段长为$L$,每个子段向前取$N$个点，即重叠部分为$L-N$，注意重叠相加法需要满足每段间至少重叠$M-1$,然后分别计算每个子段$x_k(t)$与$h(t)$的L点循环卷积$y_k(t)$,$y_k(t)$也为L点，其中前$L-N$点为混叠部分直接丢弃，仅保留后面的$N$点作为当前段的计算结果,最后一起合并起来成为$y(t)$
还是以上面的$x(t)$和$h(t)$为例，我们将$x(t)$分段，每段长8点，重叠4点：

x = np.pad(x,[4,4],mode='constant')    
x0 = x[:8]
x1 = x[4:12]
x2 = x[8:16]
x3 = x[12:20]

每段$x_k(t)$如下：

x0: [0 0 0 0 0 1 2 3]
x1: [0 1 2 3 4 5 6 7]
x2: [ 4  5  6  7  8  9 10 11]
x3: [ 8  9 10 11  0  0  0  0]

然后分别计算这4段与h的循环卷积：

y0 = circular_conv(x0,h,8)
y1 = circular_conv(x1,h,8)
y2 = circular_conv(x2,h,8)
y3 = circular_conv(x3,h,8)

每段循环卷积结果分别如下：

y0: [10 12  9  0  0  0  1  4]
y1: [34 32 22  4 10 16 22 28]
y2: [58 56 46 28 34 40 46 52]
y3: [ 0  8 25 52 58 52 33  0]

我们只取每段结果的后4个点,得到最终结果：

y: [ 0  0  1  4 10 16 22 28 34 40 46 52 58 52 33 0]

可以看到,跟整段卷积的结果是一样的。
每个子段$x_k(t)$长度为$L$，每段向前取$N$个点，重叠部分为$L-N$，$h(t)$长度为$M$的重叠保留法的计算方法python代码可以总结如下：

def overlap_save_conv(x,h,L,N):
  M = len(h) # 滤波器长度
  if L - N < M - 1: # 重叠部分至少为M-1个点
    raise ValueError('L- N must be greater than M-1')
  nb = int(np.ceil((len(x)+len(h)-1)/N)) # x分段数量
  index = np.arange(L)[None, :] + N*np.arange(nb)[:, None] #x分段索引
  x_pad = np.pad(x,[L-N,np.max(index)-len(x)],mode='constant')
  y = np.zeros((nb,N))
  for n in range(nb):
    y_n = circular_conv(x_pad[index][n],h,L) # 计算每段与h的循环卷积
    y[n] = y_n[-N:] #输出后N个点结果
  return y.ravel()

同样,我们也可以使用FFT来加速循环卷积的计算：

def overlap_save_conv(x,h,L,N):
  M = len(h) # 滤波器长度
  if L - N < M - 1: # 重叠部分至少为M-1个点
    raise ValueError('L - N must be greater than M-1')
  nb = int(np.ceil((len(x)+len(h)-1)/N)) # x分段数量
  index = np.arange(L)[None, :] + N*np.arange(nb)[:, None] # x分段索引
  x_pad = np.pad(x,[L-N,np.max(index)-len(x)],mode='constant')
  y = np.zeros((nb,N))
  H = np.fft.rfft(h,n=L)
  for n in range(nb):
    # 使用FFT计算循环卷积
    X_n = np.fft.rfft(x_pad[index][n],n=L)
    y_n = np.fft.irfft(X_n*H,n=L)
    y[n] = y_n[-N:] #输出后N个点结果
  return y.ravel()

在回声消除中频域自适应滤波器中就是使用这种方法，只不过选取的分块长度为$h(t)$的2倍，且重叠为50%

分区块重叠保留法

使用重叠保留法的时候，当$h(t)$非常长的时候，对$x(t)$分段的长度也非常长，因此这种情况也会产生比较大的延迟，以上面的$x(t)$和$h(t)$为例，我们使用重叠保留法来计算的话，最小重叠$M-1=3$点，$x(t)$分段最小的长为4,如果重叠50%的话$x(t)$分段长度最小为6。
这时我们还可以对$h(t)$进行分块，还是以上面的$x(t)$和$h(t)$为例，将$h(t)$分为$p$个子块$h_k(t)$，然后$x(t)$分别与这两小块进行卷积，然后对两个结果求和得到最终的卷积结果：

h0 = h[:2]
h1 = h[2:4]
x0 = np.pad(x,[0,2],mode='constant')
x1 = np.pad(x,[2,0],mode='constant')

y0 = np.convolve(x0,h0)
y1 = np.convolve(x1,h1)

y = y0+y1

结果如下

y: [ 0  0  1  4 10 16 22 28 34 40 46 52 58 52 33]

与整段卷积结果是一样的
然后我们再对这两个卷积分别使用重叠保留法来进行分段卷积，并使用FFT来加速循环卷积计算，就可以将$x(t)$分段分的更小，这样我们在处理时延迟就更低。
分区块的重叠保留法频域卷积python代码实现如下：

# p:分块数量
# L:分段长度
# N:帧移
def partitioned_block_overlap_save_conv(x,h,p,L,N):
  h = np.pad(h,[0,0 if len(h)%p==0 else p-len(h)%p],mode='constant')
  h = np.reshape(h,(p,-1)) #将h分为p块
  if L - N < h.shape[1] - 1:
    raise ValueError('L - N must be greater than M-1')
  mem = np.zeros((p-1)*N+L)
  index = (np.arange(L)[None, :] + N*np.arange(p)[:, None])[::-1]
  x_pad = np.pad(x,[0,len(mem)],mode='constant')
  nb = len(x_pad)//N
  y = np.zeros((nb,N))
  H = np.fft.rfft(h,n=L)
  for n in range(nb):
    mem[:-N] = mem[N:]
    mem[-N:] = x_pad[n*N:(n+1)*N]
    x_n = mem[index]
    X_n = np.fft.rfft(x_n,n=L)
    Y_n = np.sum(X_n*H,axis=0)
    y_n = np.fft.irfft(Y_n,n=L)
    y[n] = y_n[-N:]
  return y.ravel()

然后我们再对这两个卷积分别使用50%重叠的重叠保留法进行分段计算卷积，
当重叠率在50%时效率达到最高，不需要每次都对每个子块进行FFT变换，可以复用上一次的FFT变换结果，这也是为什么分区块的频域自适应滤波器一般使用50%重叠率的原因。
50%重叠率的分区块的重叠保留法python代码如下：

def half_partitioned_block_overlap_save_conv(x,h,p):
    M = len(h)
    h = np.pad(h,[0,0 if len(h)%p==0 else p-len(h)%p],mode='constant')
    h = np.reshape(h,(p,-1)) # 将h等分为p块
    N = h.shape[1] # 每块长为N
    L = 2*N # 重叠50%，x每段长L=2*N
    nb = int(np.ceil((len(x)+M-1)/N)) # x分段数量
    index = np.arange(L)[None, :] + N*np.arange(nb)[:, None] # x分段索引
    x_pad = np.pad(x,[N,np.max(index)-len(x)],mode='constant')
    y = np.zeros((nb,N))
    H = np.fft.rfft(h,n=L)
    mem = np.zeros_like(H,dtype=np.complex) # 每个h分块对应的x分段缓存
    for n in range(nb):
        # 缓存更新
        X_n = np.fft.rfft(x_pad[index][n],n=L)
        mem[1:] = mem[:-1]
        mem[0] = X_n
        # 分别计算每区块的结果然后求和
        Y_n = np.sum(mem*H,axis=0)
        y_n = np.fft.irfft(Y_n,n=L)
        y[n] = y_n[-N:] #取后N点结果
    return y.ravel()

关于频域自适应滤波可以参考我的博文：python实现LMS、NLMS、RLS、KALMAN等自适应滤波器

总结

当我们需要对音频进行实时处理，例如添加一些如音效、混响、变声等效果，或者在通话中进行回声消除、降噪等处理时，需要对信号进行卷积。这时我们便可以使用重叠相加法或者重叠保留法进行分段卷积，然后使用FFT快速计算线性卷积。这样便达到了低延时，又能节省计算量的目的。