动手深度学习-多层感知机

参考教程：https://courses.d2l.ai/zh-v2/

感知机

模型：

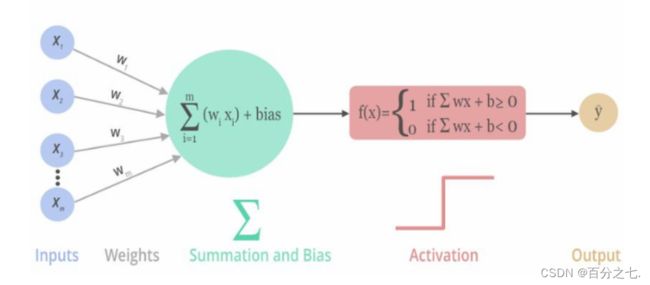
感知机模型就是一个简单的人工神经网络。
感知机是二分类的线性模型，其输入是实例的特征向量，输出的是事例的类别，分别是+1和-1，属于判别模型。它的求解算法等价于使用批量大小为1的梯度下降。

多层感知机

多层感知机（multilayer perceptron），通常缩写为MLP，也叫做全连接神经网络和深度神经网络。

这个单隐藏层的多层感知机有4个输入，3个输出，其隐藏层包含5个隐藏单元。 输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算。 因此，这个多层感知机中的层数为2。 注意，这两个层都是全连接的。 每个输入都会影响隐藏层中的每个神经元， 而隐藏层中的每个神经元又会影响输出层中的每个神经元。

激活函数

激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活， 它们将输入信号转换为输出的可微运算，引入非线性性。 大多数激活函数都是非线性的。

sigmoid函数

sigmoid函数将输入变换为区间(0, 1)上的输出。 因此，sigmoid通常称为挤压函数（squashing function）： 它将范围（-inf, inf）中的任意输入压缩到区间（0, 1）中的某个值。它是一个软的$$\sigma (x)=\{\begin{array}{ll}1& \text{ if }x>0\\ 0& \text{ otherwise }\end{array}$$图像如下图，它在0处不好求导。sigmoid解决了这一问题，是他的soft版本。

$$\mathrm{sigmoid}(x)=\frac{1}{1+\exp (-x)}$$

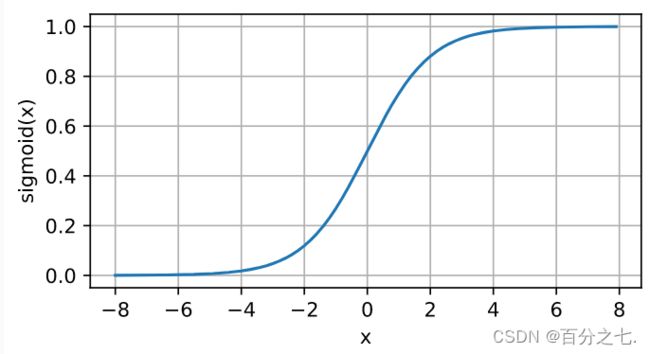
当输入接近0时，sigmoid函数接近线性变换。

tanh函数

与sigmoid函数类似， tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。 tanh函数的公式如下：
$$\tanh (x)=\frac{1-\exp (-2x)}{1+\exp (-2x)}$$
函数的形状类似于sigmoid函数， 不同的是tanh函数关于坐标系原点中心对称。

ReLU函数

最受欢迎的激活函数是修正线性单元（Rectified linear unit，ReLU），因为它实现简单，运算特别快，不用进行指数运算，同时在各种预测任务中表现良好。$$\mathrm{ReLU}(x)=\max (x,0)$$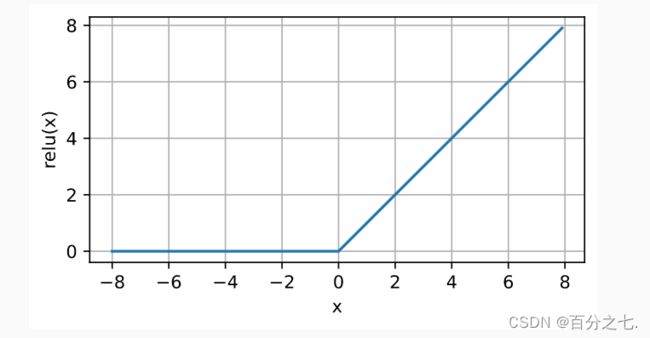
当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。 注意，当输入值精确等于0时，ReLU函数不可导。

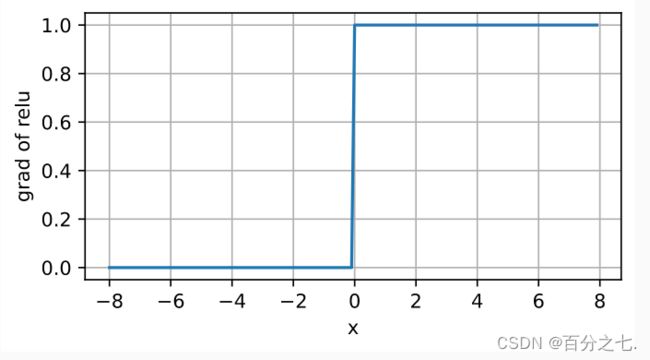
使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。 这使得优化表现得更好，并且ReLU减轻了困扰以往神经网络的梯度消失问题（以后介绍）。
总结：

• 多层感知机使用隐藏层和激活函数来得到非线性模型。
• 常用激活函数是Sigmoid，Tanh，ReLU(最简单、用的多)

多层感知机的简洁实现

#通过高级API更简洁地实现多层感知机
import torch
from torch import nn
from d2l import torch as d2l
#模型
#与softmax回归的简洁实现相比，唯一的区别是我们添加了2个全连接层。第一层是隐藏层，它包含256个隐藏单元，并使用了ReLU激活函数。第二层是输出层。
net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')#交叉熵损失函数
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

• 对于相同的分类问题，多层感知机的实现与softmax回归的实现相同，只是多层感知机的实现里增加了带有激活函数的隐藏层。