强化学习蘑菇书Easy RL第二、三章学习(马尔可夫决策过程、表格型方法)
马尔可夫决策过程概述
Markov Process(MP)通常来说是未来状态的条件概率分布仅依赖于当前的状态。在离散随机过程里,我们需要把随机变量所有可能取值的集合放到一个状态空间里,在强化学习里,我们直接用状态转移的概率来表示:
p ( s t + 1 ∣ s t ) = p ( s t + 1 ∣ h t ) p ( s t + 1 ∣ s t , a t ) = p ( s t + 1 ∣ h t , a t ) \begin{aligned} p\left(s_{t+1} \mid s_{t}\right) &=p\left(s_{t+1} \mid h_{t}\right) \\ p\left(s_{t+1} \mid s_{t}, a_{t}\right) &=p\left(s_{t+1} \mid h_{t}, a_{t}\right) \end{aligned} p(st+1∣st)p(st+1∣st,at)=p(st+1∣ht)=p(st+1∣ht,at)
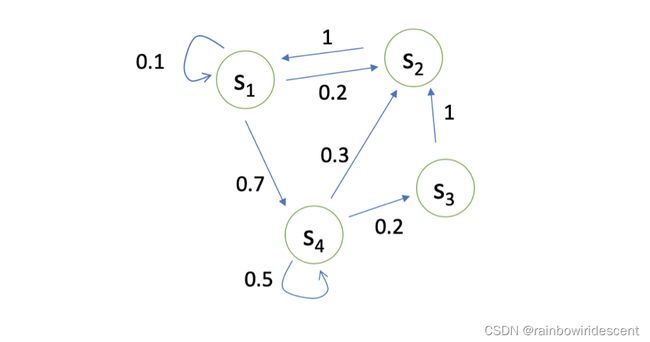
如上图所示,离散的马尔可夫链有四个状态,而这四个状态就在s1,s2,s3和s4中互相转移。而转移概率就在上图用箭头表示出来了,对于不同的状态采样,我们可以生成许多的轨迹。
简单地,我们可以用一个状态转移矩阵来表示:
P = [ P ( s 1 ∣ s 1 ) P ( s 2 ∣ s 1 ) … P ( s N ∣ s 1 ) P ( s 1 ∣ s 2 ) P ( s 2 ∣ s 2 ) … P ( s N ∣ s 2 ) ⋮ ⋮ ⋱ ⋮ P ( s 1 ∣ s N ) P ( s 2 ∣ s N ) … P ( s N ∣ s N ) ] P=\left[\begin{array}{cccc} P\left(s_{1} \mid s_{1}\right) & P\left(s_{2} \mid s_{1}\right) & \ldots & P\left(s_{N} \mid s_{1}\right) \\ P\left(s_{1} \mid s_{2}\right) & P\left(s_{2} \mid s_{2}\right) & \ldots & P\left(s_{N} \mid s_{2}\right) \\ \vdots & \vdots & \ddots & \vdots \\ P\left(s_{1} \mid s_{N}\right) & P\left(s_{2} \mid s_{N}\right) & \ldots & P\left(s_{N} \mid s_{N}\right) \end{array}\right] P=⎣ ⎡P(s1∣s1)P(s1∣s2)⋮P(s1∣sN)P(s2∣s1)P(s2∣s2)⋮P(s2∣sN)……⋱…P(sN∣s1)P(sN∣s2)⋮P(sN∣sN)⎦ ⎤
Markov Reward Process
下面这一小节我们来聊一下马尔科夫奖励过程。两个新的概念:
1.回报:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + γ 3 R t + 4 + … + γ I ′ − t − 1 R T G_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} R_{t+4}+\ldots+\gamma^{I^{\prime}-t-1} R_{T} Gt=Rt+1+γRt+2+γ2Rt+3+γ3Rt+4+…+γI′−t−1RT
越往后得到的奖励,折扣越多。
2.状态价值函数:
V t ( s ) = E [ G t ∣ s t = s ] = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + … + γ T − t − 1 R T ∣ s t = s ] \begin{aligned} V_{t}(s) &=\mathbb{E}\left[G_{t} \mid s_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots+\gamma^{T-t-1} R_{T} \mid s_{t}=s\right] \end{aligned} Vt(s)=E[Gt∣st=s]=E[Rt+1+γRt+2+γ2Rt+3+…+γT−t−1RT∣st=s]
状态价值函数被定义成回报的期望,也就是从这个状态开始,可以获得多大的价值。
使用折扣因子的目的:
- 避免无穷的奖励
- 不一定完全信任模型,模型带有不确定性
- 更想要及时获得奖励
(因此,折扣因子通常作为一个强化学习智能体的超参数来调整,通过调整折扣因子,我们可以得到不同动作的智能体)
The use of a reward signal to formalize the idea of a goal is one of the most distinctive features of reinforcement learning.
如下图,状态转移图所示,这里,实心正方形表示对应于一集结束的特殊吸收状态。从S0开始,我们得到奖励序列+1,+1,+1,0,0,0。把这些加起来,无论我们在第一个T奖励(这里T=3)上求和,还是在整个无限序列上求和,我们都会得到相同的回报。

贝尔曼方程
这里比较难,我也理解的时间很长。。。
然后看了祖师爷sutton的书又找了一些例子来补充学习。
首先是先回顾了一下全期望公式,找了个例子来推导证明。
E [ V ( s t + 1 ) ∣ s t ] = E [ E [ G t + 1 ∣ s t + 1 ] ∣ s t ] = E [ G t + 1 ∣ s t ] \mathbb{E}\left[V\left(s_{t+1}\right) \mid s_{t}\right]=\mathbb{E}\left[\mathbb{E}\left[G_{t+1} \mid s_{t+1}\right] \mid s_{t}\right]=E\left[G_{t+1} \mid s_{t}\right] E[V(st+1)∣st]=E[E[Gt+1∣st+1]∣st]=E[Gt+1∣st]
以下为推导:
E [ E [ G t + 1 ∣ s t + 1 ] ∣ s t ] = E [ E [ g ′ ∣ s ′ ] ∣ s ] = E [ ∑ g ′ g ′ p ( g ′ ∣ s ′ ) ∣ s ] = ∑ s ′ ∑ g ′ g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ ∣ s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ ∣ s ) p ( s ) p ( s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ , s ) p ( s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ , s ′ , s ) p ( s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ , s ′ ∣ s ) = ∑ g ′ ∑ s ′ g ′ p ( g ′ , s ′ ∣ s ) = ∑ g ′ g ′ p ( g ′ ∣ s ) = E [ g ′ ∣ s ] = E [ G t + 1 ∣ s t ] \begin{aligned} \mathbb{E}\left[\mathbb{E}\left[G_{t+1} \mid s_{t+1}\right] \mid s_{t}\right] &=\mathbb{E}\left[\mathbb{E}\left[g^{\prime} \mid s^{\prime}\right] \mid s\right] \\ &=\mathbb{E}\left[\sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s^{\prime}\right) \mid s\right] \\ &=\sum_{s^{\prime}} \sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime} \mid s\right) \\ &=\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime} \mid s\right) p(s)}{p(s)} \\ &=\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime}, s\right)}{p(s)} \\ &=\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime}, s^{\prime}, s\right)}{p(s)} \\ &=\sum_{s^{\prime}} \sum_{g^{\prime}} g^{\prime} p\left(g^{\prime}, s^{\prime} \mid s\right) \\ &=\sum_{g^{\prime}} \sum_{s^{\prime}} g^{\prime} p\left(g^{\prime}, s^{\prime} \mid s\right) \\ &=\sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s\right) \\ &=\mathbb{E}\left[g^{\prime} \mid s\right]=\mathbb{E}\left[G_{t+1} \mid s_{t}\right] \end{aligned} E[E[Gt+1∣st+1]∣st]=E[E[g′∣s′]∣s]=E⎣ ⎡g′∑g′p(g′∣s′)∣s⎦ ⎤=s′∑g′∑g′p(g′∣s′,s)p(s′∣s)=s′∑g′∑p(s)g′p(g′∣s′,s)p(s′∣s)p(s)=s′∑g′∑p(s)g′p(g′∣s′,s)p(s′,s)=s′∑g′∑p(s)g′p(g′,s′,s)=s′∑g′∑g′p(g′,s′∣s)=g′∑s′∑g′p(g′,s′∣s)=g′∑g′p(g′∣s)=E[g′∣s]=E[Gt+1∣st]
注:为简化,去掉了t,且都用了小写变量字母表示,具体可参照公式第一行。
若有疑问可自行查看概率论与数理统计书or百度一下。
然后是Bellman方程:
V ( s ) = E [ G t ∣ s t = s ] = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + … ∣ s t = s ] = E [ R t + 1 ∣ s t = s ] + γ E [ R t + 2 + γ R t + 3 + γ 2 R t + 4 + … ∣ s t = s ] = R ( s ) + γ E [ G t + 1 ∣ s t = s ] = R ( s ) + γ E [ V ( s t + 1 ) ∣ s t = s ] = R ( s ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s ) V ( s ′ ) \begin{aligned} V(s) &=\mathbb{E}\left[G_{t} \mid s_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid s_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1} \mid s_{t}=s\right]+\gamma \mathbb{E}\left[R_{t+2}+\gamma R_{t+3}+\gamma^{2} R_{t+4}+\ldots \mid s_{t}=s\right] \\ &=R(s)+\gamma \mathbb{E}\left[G_{t+1} \mid s_{t}=s\right] \\ &=R(s)+\gamma \mathbb{E}\left[V\left(s_{t+1}\right) \mid s_{t}=s\right] \\ &=R(s)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s\right) V\left(s^{\prime}\right) \end{aligned} V(s)=E[Gt∣st=s]=E[Rt+1+γRt+2+γ2Rt+3+…∣st=s]=E[Rt+1∣st=s]+γE[Rt+2+γRt+3+γ2Rt+4+…∣st=s]=R(s)+γE[Gt+1∣st=s]=R(s)+γE[V(st+1)∣st=s]=R(s)+γs′∈S∑P(s′∣s)V(s′)
Bellman Equation 定义的就是当前状态跟未来状态的一个迭代的关系。
* V ( s ′ ) V\left(s^{\prime}\right) V(s′)向量是我们当前的状态,我们需要乘以转移矩阵,然后再加上对应的奖励,得到现在的状态。或者说,在强化学习和动态规划中使用的值函数的一个基本特性是,它们满足特定的递归关系。
当我们要处理的MRP很小量时,对应的复杂度也很小,我们就可以考虑把贝尔曼方程写成矩阵的形式,然后通过求逆矩阵的方式,写出解析解。
但是,如果状态很多的MRP,就不能解出来了。在这种情况下可以采用的方法有:蒙特卡洛法、动态规划法。
马尔可夫决策
当多了decison时,还需要加一个action,也就是说,**你当前的状态以及你采取的动作会决定你在当前可能得到的奖励多少。**另外,已知一个 MDP 和一个 policy π \pi π 的时候,我们可以把 MDP 转换成 MRP。
这里补充理解进去:
马尔可夫决策过程不是直接通过转移概率决定下一个状态,而是多了一层动作a,简言之,马尔科夫决策多了一层决策性,动作是由智能体决定的。

价值函数的定义:

We call the function vπ the state-value function for policy π,策略π下,该式子描述了状态价值函数。
类似地,我们定义了在策略π下的状态s中采取行动a的值,表示为qπ(s,a),作为从s开始的预期回报,采取行动a,然后遵循策略π:
q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s , A t = a ] q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s, A_{t}=a\right] qπ(s,a)=Eπ[Gt∣St=s,At=a]=Eπ[∑k=0∞γkRt+k+1∣St=s,At=a]
补充一下sutton书里的例子(备份图),每个开口圆代表一个状态,每个实心圆代表一个状态-动作对。从状态s(顶部的根节点)开始,agent可以采取图3.4a中所示的三种操作中的任何一种。从每种状态中,环境都可以响应接下来的几个状态之一s0,以及奖励r。Bellman方程对所有可能性进行平均,并根据其发生的概率对每个状态进行加权。开始状态的值必须等于预期下一个状态的(折扣)值,加上沿途预期的奖励。

另外,这些操作将值信息从其后续状态(或状态-动作对)传输回状态(或状态-动作对)。我们在整本书中使用备份图来提供我们讨论的算法的图形摘要。(注意,与转换图不同,备份图的状态节点不一定代表不同的状态;例如,一个状态可能是它自己的后续状态。省略了显式箭头,因为时间在备份图中总是向下流动。)
Q函数在备份图中的分解部分,先略了。。
Prediction & Control
这部分还挺重要的,可以说是MDP中的核心了,我们输入元组与策略以后,输出的是价值函数。
控制的话,输出的应该是一个最佳的价值函数和最佳的策略。(嘎嘎,有点优化的味道了,很喜欢,和专业好像哈哈哈)
要强调的是,这两者的区别就在于,
预测问题是给定一个 policy,我们要确定它的 value function 是多少。
而控制问题是在没有 policy 的前提下,我们要确定最优的 value function 以及对应的决策方案。
实际上,这两者是递进的关系,在强化学习中,我们通过解决预测问题,进而解决控制问题。
我们再来看一个动态的例子,用了斯坦福大学里面的,GridWorld DP Demo ,这个网站模拟了单步更新的过程中,所有格子的一个状态价值的变化过程。
policy evaluation(一步迭代)的结果:
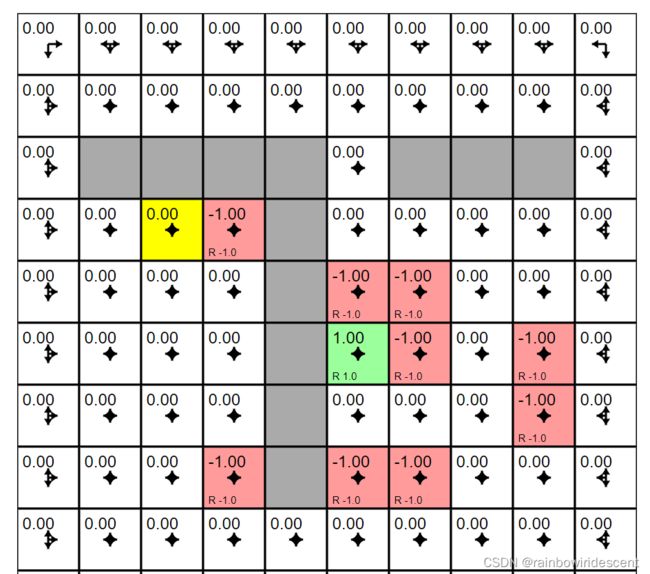
相应代码:
evaluatePolicy: function() {
// perform a synchronous update of the value function
var Vnew = zeros(this.ns); // initialize new value function array for each state
for(var s=0;s < this.ns;s++) {
var v = 0.0;
var poss = this.env.allowedActions(s); // fetch all possible actions
for(var i=0,n=poss.length;i < n;i++) {
var a = poss[i];
var prob = this.P[a*this.ns+s]; // probability of taking action under current policy
var ns = this.env.nextStateDistribution(s,a); // look up the next state
var rs = this.env.reward(s,a,ns); // get reward for s->a->ns transition
v += prob * (rs + this.gamma * this.V[ns]);
}
Vnew[s] = v;
}
this.V = Vnew; // swap
},
我自己试了一下,这是点toggle value iteration时候的结果。。。
这是切换成了价值迭代,后面会再说明。
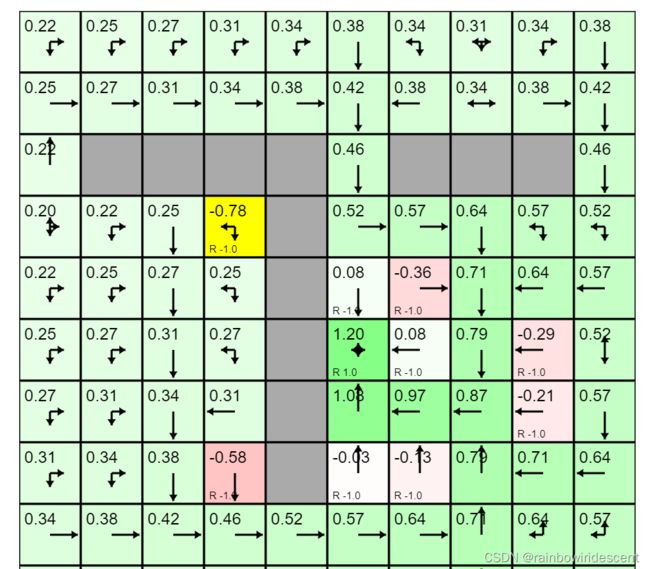
再说一下控制吧,寻找一个最优的价值函数(max),再寻找最优policy

搜索最佳策略有两种常用的方法:policy iteration 和 value iteration。
策略迭代的核心是策略评估+策略改进,价值迭代主要运用了最优性原理。这里具体的对比与贝尔曼方程不再赘述。
如果是一个 prediction 的问题,即 policy evaluation 的问题,直接就是不停地 run 这个 Bellman Expectation Equation,这样我们就可以去估计出给定的这个策略,然后得到价值函数。
对于 control,
如果采取的算法是 policy iteration,那这里用的是 Bellman Expectation Equation 。把它分成两步,先上它的这个价值函数,再去优化它的策略,然后不停迭代。这里用到的只是 Bellman Expectation Equation。
如果采取的算法是 value iteration,那这里用到的 Bellman Equation 就是 Bellman Optimality Equation,通过 arg max 这个过程,不停地去 arg max 它,最后它就会达到最优的状态。
简单用一个表格总结一下:
| 问题 | 算法 |
|---|---|
| 预测 | 迭代策略评估(贝尔曼方程) |
| 控制 | 策略迭代(贝尔曼期望方程)、价值迭代(贝尔曼最优方程) |
本章关键词:马尔可夫性质、马尔可夫链、状态转移矩阵、马尔可夫奖励过程、汇报、贝尔曼方程、动态规划算法、马尔可夫决策中的prediction&control。
啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊这里搞一个分割线。。。。。。
################################################
终于第三章了,内容也太多了。
表格型方法
策略最简单的表示是查找表(look-up table),即表格型策略(tabular policy)。使用查找表的强化学习方法称为表格型方法(tabular method),如蒙特卡洛、Q学习和Sarsa。本章通过最简单的表格型方法来讲解如何使用基于价值的方法求解强化学习问题。
有模型vs免模型
这个点在上一篇博客,强化学习概论里面也提到了,在RL里,可以作为一种简单的分类方式。
环境,是通过概率函数与奖励函数来描述的。如果我们知道环境的状态转移概率和奖励函数,就可以认为这个环境是已知的,因为我们用这两个函数来描述环境。如果环境是已知的,我们其实可以用动态规划算法去计算,某个情形下,概率最大的最佳策略是什么。
很多强化学习的经典算法都是免模型的,也就是环境是未知的。 我们处在未知的环境里,也就是这一系列的决策的概率函数和奖励函数是未知的,这就是有模型与免模型的最大的区别。强化学习用价值函数 V来表示状态是好的还是坏的,用 Q 函数来判断在什么状态下采取什么动作能够取得最大奖励,即用 Q 函数来表示状态-动作值。
关于免模型,再说明一下:
当马尔可夫决策过程的模型未知或者模型很大时,我们可以使用免模型强化学习的方法。免模型强化学习方法没有获取环境的状态转移和奖励函数,而是让智能体与环境进行交互,采集大量的轨迹数据,智能体从轨迹中获取信息来改进策略,从而获得更多的奖励。
有一点点类似于上一节中让小船去获取轨迹的例子。。。
在强化学习中,我们最终要求解的就是一张 Q 表格,它的行数是所有状态的数量,一般可以用坐标来表示格子的状态,也可以用 1、2、3、4、5、6、7 来表示不同的位置。Q 表格的列表示上、下、左、右4个动作。 最开始的时候,Q 表格会全部初始化为0。智能体会不断和环境交互得到不同的轨迹,当交互的次数足够多的时候,我们就可以估算出每一个状态下,每个动作的平均总奖励,进而更新 Q 表格。Q表格的更新就是接下来要引入的强化概念。
嗯。。。继续了
强化是指我们可以用下一个状态的价值来更新当前状态的价值,其实就是强化学习里面自举的概念。在强化学习里面,我们可以每走一步更新一次 Q 表格,用下一个状态的 Q 值来更新当前状态的 Q 值,这种单步更新的方法被称为时序差分方法。这种方法,是免模型的一种。
可以比较的是巴甫洛夫给小狗的实验,类似于一种延迟奖励。小狗本来不觉得铃声有价值的,经过强化之后,小狗就会慢慢地意识到铃声也是有价值的,它可能带来食物。更重要的是当一种条件反射巩固之后,我们再用另外一种新的刺激和条件反射相结合,还可以形成第二级条件反射,同样地还可以形成第三级条件反射。
我们先初始化,然后开始时序差分方法的更新过程。 在训练的过程中,小黄球在不断地试错,在探索中会先迅速地发现有奖励的格子。最开始的时候,有奖励的格子才有价值。当小黄球不断地重复走这些路线的时候,有价值的格子可以慢慢地影响它附近的格子的价值。 反复训练之后,有奖励的格子周围的格子的状态就会慢慢被强化。强化就是价值最终收敛到最优的情况之后,小黄球就会自动往价值高的格子走,就可以走到能够拿到奖励的格子。
以下是斯坦福时序差分的网格demo:
// create environment
env = new Gridworld();
// create the agent, yay!
var spec = { alpha: 0.01 } // see full options on top of this page
agent = new RL.TDAgent(env, spec);
setInterval(function(){ // start the learning loop
var action = agent.act(s); // s is an integer, action is integer
// execute action in environment and get the reward
agent.learn(reward); // the agent improves its Q,policy,model, etc.
}, 0);
时序差分,不需要马尔可夫决策过程的转移矩阵和奖励函数。 此外,时序差分方法可以从不完整的回合中学习,并且结合了自举的思想。
用一个公式来加深一下理解:
V ( s t ) ← V ( s t ) + α ( r t + 1 + γ V ( s t + 1 ) − V ( s t ) ) V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left(r_{t+1}+\gamma V\left(s_{t+1}\right)-V\left(s_{t}\right)\right) V(st)←V(st)+α(rt+1+γV(st+1)−V(st))
对于某个给定的策略pai,我们算出它的价值函数 V。 每往前走一步,就做一步自举,用得到的估计回报来更新上一时刻的值。

稍微总结对比一下与蒙特卡洛的优劣势:
MC优势:1.从episode经历里直接学习。2.免模型 3.value为mean return。
MC劣势:1.使用蒙特卡洛方法有episodic马尔可夫过程假设。2.相比于TD学习速度慢。
TD优势:1.从episode经历里直接学习,可以从不完整序列中学习。2.免模型 3.不需要得到最后输出结果,每一步在线学习。4.适合于连续空间强化学习。
TD劣势:用自举抽样每个episode不够准确。本身拟合就不确定了。
下图为n步的时序差分:
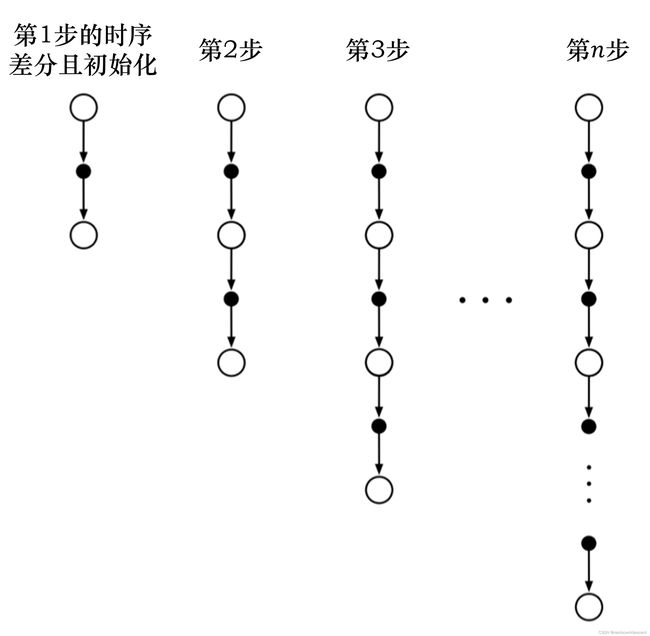
粗略地说,蒙特卡洛方法使用(6.3)的估计作为目标,而DP方法使用(6.4)的估计作为目标。蒙特卡洛目标是一个估计值,因为(6.3)中的预期值未知;使用样本回报代替实际预期回报。DP目标是一个估计值,不是因为预期值(假设由环境模型完全提供),而是因为vπ(St+1)未知,而是使用当前估计值v(St+1)。TD目标是一个估计值,有两个原因:它对(6.4)中的预期值进行采样,并使用当前估计值V而不是真实的Vπ。因此,TD方法将蒙特卡洛采样与DP自举相结合。
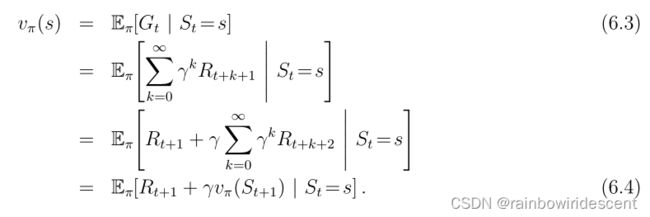
Sarsa和Q学习
Q学习是异策略的时序差分学习方法,Sarsa 是同策略的时序差分学习方法。
Sarsa算法流程:

简单说一下Q学习,主要是两种策略,target policy和behavior policy,后面的实验cliffwalking也是用Q学习来实现的。
我们的目标策略π,在Q表格上使用greedy的policy,就可以直接生成下一步的所有状态。可以说,这种异策略学习是一种探索机制,学习的效率也比较高,而且也不完全是随机的,不断基于Q表格来改进,所以也体现“强化”的特点。。
嗯。。。Q学习的增量学习公式啥的还没推导完,回头再更新笔记好了。
先把实验做完。
Cliffwalking实验(项目一)
了解了环境以后,我们直接在代码中定义:
import gym #导入gym库
from envs.gridworld_env import CliffWalkingWapper #这一步导入自定义的装饰器
env = gym.make('CliffWalking-v0) #定义环境
env = CliffWalkingWapper(env) #装饰环境
n_states = env.observation_space.n
n_actions = env.action_space.n
print(f"state_numbers:{n_states},action_numbers:{n_actions}")
结果:

状态数48,这里设置智能体当前所在网格的一个编号,动作数4表示我们有0123这四个数分别对应上下左右四个动作。
然后我们初始化环境来输出一下当前的状态:
state = env.reset()
print(f"initial_state:{state}")
结果如下:
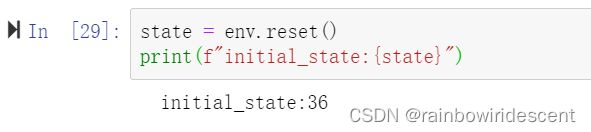
这里表示的就是当前agent在网格编号36,也就是起点。
接下来是学习一下强化学习的基本接口。
一般强化学习的训练模式的steps:
1)初始化环境、智能体
2)对于每个回合,智能体选取动作
3)环境接受动作反馈信息下一个状态和奖励
4)智能体进行policy update(learning)
5)多个回合后,算法收敛,保存模型,用于后续的分析和画图
'''初始化环境'''
env = gym.make("CliffWalking-v0") # 定义环境
env = CliffWalkingWapper(env) #装饰环境
env.seed(1) #设置随机种子
n_states = env.observation_space.n #状态数
n_actions = env.action_space.n #动作数
agent = QLearning(n_states,n_actions,cfg)
for i_ep in range(cfg.train_eps): #cfg.train_eps表示最大的训练回合数
enp_reward=0 #记录回合的奖励
state = env.reset()#重置环境
while True:
action = agent.choose_action(state)# 选动作
next_state,reward,done,_ = env.step(action)
# 环境根据动作反馈的reward和下一个state
agent.update(state,action,reward,next_state,done)
state = next_state #更新
ep_reword +=reward
if done:
break
Q学习的算法具体实现,主要是两件事,一个是选择动作,一个是更新策略,定义一个Qlearning类以后,主要包含两个函数,choose_action()还有update()
我们来看一下这两个函数的定义方式,第一步是动作的选择:
def choose_action(self, state):
self.sample_count += 1
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \
math.exp(-1. * self.sample_count / self.epsilon_decay) # epsilon是会递减的,这里选择指数递减
# e-greedy 策略
if np.random.uniform(0, 1) > self.epsilon:
action = np.argmax(self.Q_table[str(state)]) # 选择Q(s,a)最大对应的动作
else:
action = np.random.choice(self.n_actions) # 随机选择动作
return
使用epsilion-greedy策略选择动作,具体怎么弄的,有点像我之前提到的,探索机制,我们输入目前的状态,用if来判断一下这个随机值是不是>self.epsilion(我们设置的),然后选取最大的Q(s,a)对应的动作。
选择完动作后,然后再来看一下qlearning.py中比较重要的另一个函数,策略更新函数。
代码如下:
def update(self, state, action, reward, next_state, done):
Q_predict = self.Q_table[str(state)][action]
if done: # 终止状态
Q_target = reward
else:
Q_target = reward + self.gamma * np.max(self.Q_table[str(next_state)])
self.Q_table[str(state)][action] += self.lr * (Q_target - Q_predict)
这里实现的逻辑就是伪代码中的更新公式。
具体的项目代码在github上。。。
附上链接:
https://github.com/datawhalechina/easy-rl/tree/master/codes/QLearning
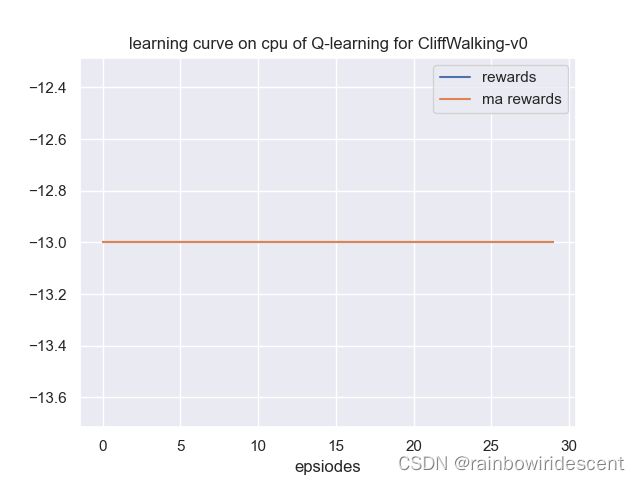
训练结果:
模型很快收敛
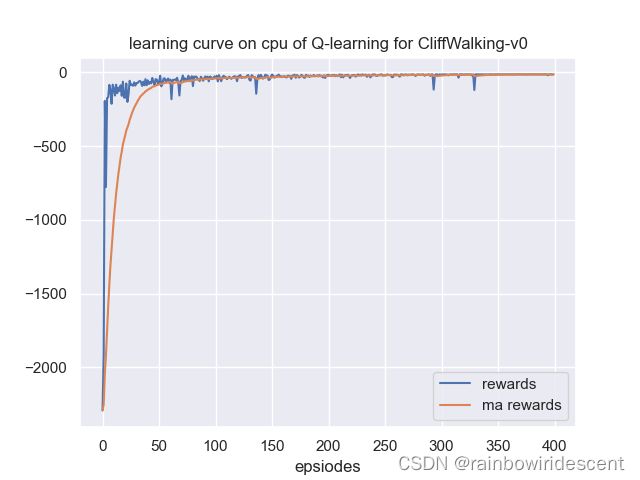
害,没写完。。好多公式细节都没写进去,先这样发布,回头再接着补,
总之,对于小白来说,还有很大的进步空间。。。。
加油啊!!!
Ref:
【1】https://datawhalechina.github.io/easy-rl/#/chapter2/chapter2
【2】https://datawhalechina.github.io/easy-rl/#/chapter3/chapter3
【3】https://zhuanlan.zhihu.com/c_135909947
【4】https://www.zhihu.com/question/62388365
【5】SUTTON R S,BARTO AG.Reinforcement Learning:An introduction (second edition) [M].London: The MIT Press,2018
【6】邱锡鹏.神经网络与深度学习[M].北京:机械工业出版社,2020
【7】https://www.davidsilver.uk/teaching/
【8】王琦等,Easy RL蘑菇书,强化学习教程