stata：DID双重差分模型基础作业

目录

一、双重差分模型（DID）基本介绍

1.1传统DID模型

(1）传统命令

(2)  外部命令:diff

1.2双向固定DID模型（更常用）

(1) reg

(2) xtreg

(3) areg

二、DID的检验

2.1DID的三个前提假设

2.2平行趋势检验（动态效应检验）

2.3政策外生性检验

2.4安慰剂检验

三、实证过程

---

以下题为例：

核心变量的描述性统计：

· sum

可以得出id为个体变量，year为时间变量，treatment为分组虚拟变量，post为分期虚拟变量，did为treatment和post的交互项；

. sum id year treatment post did lnpgdp 

    Variable |        Obs        Mean    Std. dev.       Min        Max
-------------+---------------------------------------------------------
          id |        735          25    14.15177          1         49
        year |        735        2009    4.323436       2002       2016
   treatment |        735    .1428571    .3501654          0          1
        post |        735    .2666667    .4425178          0          1
         did |        735    .0380952    .1915566          0          1
-------------+---------------------------------------------------------
      lnpgdp |        735    9.852075    .9338246   7.095918   11.77851

一、双重差分模型（DID）基本介绍

DID的两种常见形式

注意：

1.区分分期虚拟变量（政策实施虚拟变量）和时间虚拟变量；前者只有0和1两种取值，代表是否实施了政策，而后者则是区分各种不同的时间，通常T个时间段有T-1个时间虚拟变量。相应有 分期效应 和 时间效应 两种。

2.区分分组虚拟变量和个体变量；前者只有0和1两种取值，代表是否属于处理组，后者则是区分不同的个体。相应的也有 组间异质性 和 个体异质性 两种。

3.DID模型不要求政策实施前后所选的样本完全一致。（若一致，可以使用双向固定DID模型；若不一致，使用传统DID模型）

1.1传统DID模型：

适用范围：非面板模型，在政策实施前后选用的样本不相同（只要保证时间趋势相同即可）。此时，个体效应和时间效应分别用对应的分组和政策实施时间虚拟变量来粗糙替代。

(1）传统命令

· reg y did X i.t i.dt,r

t：分组虚拟变量，t=0为treatment组，t=1为control组
dt：政策实施时间虚拟变量
did：t*dt 双重差分模型的核心解释变量
X：控制变量
i.t：粗糙的组间异质性，替代个体效应；
i.dt：粗糙的分期时间效应，替代时间效应；

(2)  外部命令:diff

· diff y,treat(t) period(dt) cov(X) robust

1.2双向固定DID模型（更常用）

适用范围：面板模型，在政策实施前后研究的样本保持不变。此时，个体效应与个体效应的设置与双向固定面板效应类似。

法一：reg

reg lnpgdp did $cv i.id i.year,vce(cluster id) 
//$cv为使用设定的全局变量（此处为控制变量）

Linear regression                               Number of obs     =        608
                                                F(21, 43)         =          .
                                                Prob > F          =          .
                                                R-squared         =     0.9800
                                                Root MSE          =     .12897

                                    (Std. err. adjusted for 44 clusters in id)
------------------------------------------------------------------------------
             |               Robust
      lnpgdp | Coefficient  std. err.      t    P>|t|     [95% conf. interval]
-------------+----------------------------------------------------------------
         did |   .1612596   .0424702     3.80   0.000     .0756103    .2469089
      popden |   -2.83359   4.271172    -0.66   0.511    -11.44723    5.780049
         sav |   -.826351   .1212829    -6.81   0.000    -1.070941   -.5817607
    industry |    .123654   .0352388     3.51   0.001     .0525882    .1947198
    non_agri |  -1.220827   .3814877    -3.20   0.003    -1.990171   -.4514841
     welfare |  -.0013941   .0021004    -0.66   0.510      -.00563    .0028417
         fdi |  -.4705762   .6373817    -0.74   0.464    -1.755979    .8148265
         exp |   .1311563   .0920516     1.42   0.161    -.0544835     .316796
             |
          id |
          2  |   -.599242   .0829293    -7.23   0.000    -.7664849    -.431999
          3  |  -.4309197   .0438624    -9.82   0.000    -.5193766   -.3424628
          4  |   .0159189   .0823923     0.19   0.848    -.1502411    .1820789
          5  |   .6129284   .2612016     2.35   0.024     .0861651    1.139692
          6  |   .8708063   .1940028     4.49   0.000     .4795624     1.26205
          7  |   .5938385   .1355898     4.38   0.000     .3203956    .8672815
          8  |   .5970364   .1555135     3.84   0.000     .2834135    .9106592
          9  |  -.2133781   .0503604    -4.24   0.000    -.3149395   -.1118168
         10  |  -.2149078   .0947671    -2.27   0.028    -.4060239   -.0237918
         11  |   .9978647   .2299034     4.34   0.000     .5342202    1.461509
         12  |  -.4611409   .1524103    -3.03   0.004    -.7685055   -.1537763
         13  |  -.4717708   .1328164    -3.55   0.001    -.7396206    -.203921
         14  |  -.5159563   .1206059    -4.28   0.000    -.7591813   -.2727313
         15  |  -.2170632   .1307039    -1.66   0.104    -.4806527    .0465263
         16  |  -.2670158   .1208296    -2.21   0.032     -.510692   -.0233396
         17  |  -.1888095   .1052775    -1.79   0.080    -.4011217    .0235027
         18  |   .4277456   .0532271     8.04   0.000     .3204029    .5350884
         19  |   .1488939   .0929514     1.60   0.117    -.0385606    .3363483
         20  |    -.32777   .0613168    -5.35   0.000    -.4514272   -.2041129
         21  |  -.7692016   .0676439   -11.37   0.000    -.9056186   -.6327847
         22  |   -.226435   .0549437    -4.12   0.000    -.3372396   -.1156304
         23  |  -.2079738   .0505605    -4.11   0.000    -.3099389   -.1060088
         24  |  -.1715741   .0949496    -1.81   0.078    -.3630582    .0199099
         25  |   .4029898   .0995619     4.05   0.000     .2022042    .6037754
         26  |  -.6548432   .1240178    -5.28   0.000     -.904949   -.4047374
         27  |  -.8356669   .1082983    -7.72   0.000    -1.054071   -.6172625
         28  |  -.2335387   .0645286    -3.62   0.001    -.3636731   -.1034043
         29  |  -.0778349   .0310321    -2.51   0.016    -.1404171   -.0152528
         30  |  -.1241396   .0507693    -2.45   0.019    -.2265257   -.0217535
         31  |  -.2122203   .1101972    -1.93   0.061    -.4344542    .0100135
         32  |  -.5505511   .0650699    -8.46   0.000    -.6817771   -.4193251
         33  |  -.8061707   .1096685    -7.35   0.000    -1.027338   -.5850032
         34  |  -.1823216    .199542    -0.91   0.366    -.5847364    .2200932
         35  |   .3302556   .2543698     1.30   0.201    -.1827301    .8432412
         36  |  -.1942807   .0642742    -3.02   0.004     -.323902   -.0646594
         37  |  -.9824465   .0676922   -14.51   0.000    -1.118961   -.8459321
         38  |  -.3232847   .1119534    -2.89   0.006    -.5490601   -.0975092
         39  |  -.7595989   .0737988   -10.29   0.000    -.9084284   -.6107694
         40  |  -.3370776   .1204593    -2.80   0.008     -.580007   -.0941483
         41  |  -.1841472   .0937726    -1.96   0.056    -.3732576    .0049632
         42  |  -.1523469   .0816846    -1.87   0.069    -.3170796    .0123858
         43  |  -.7588555   .1185358    -6.40   0.000    -.9979058   -.5198053
         44  |  -.1398632   .0957483    -1.46   0.151    -.3329581    .0532318
             |
        year |
       2003  |   .0867016   .0177547     4.88   0.000     .0508958    .1225074
       2004  |   .1497615   .0234327     6.39   0.000     .1025051     .197018
       2005  |   .2401505   .0370452     6.48   0.000     .1654417    .3148593
       2006  |    .285288   .0475912     5.99   0.000     .1893112    .3812649
       2007  |   .4044815   .0519725     7.78   0.000      .299669    .5092939
       2008  |    .618554    .064974     9.52   0.000     .4875215    .7495865
       2009  |   .7602133   .0720347    10.55   0.000     .6149415    .9054851
       2010  |   .9474614   .0787456    12.03   0.000     .7886558    1.106267
       2011  |    1.12886   .0840711    13.43   0.000     .9593141    1.298405
       2012  |   1.230967   .0942061    13.07   0.000     1.040982    1.420952
       2013  |   1.302292   .1021949    12.74   0.000     1.096196    1.508387
       2014  |   1.283281    .116348    11.03   0.000     1.048643    1.517919
       2015  |   1.397266   .1128194    12.38   0.000     1.169744    1.624788
       2016  |   1.489624   .1268996    11.74   0.000     1.233706    1.745541
             |
       _cons |   8.934893    .445487    20.06   0.000     8.036483    9.833303
------------------------------------------------------------------------------

法二：xtreg

xtset id year //设定面板模型的时间和个体
xreg lnpgdp did $cv i.year,vce(cluster id) 

法三：areg

优点：相比较上述两种方法，可以省去个体效应的估计结果，大大提升运行效率。

areg lnpgdp did $cv i.year,absorb(id) vce(cluster id) 

Linear regression, absorbing indicators             Number of obs     =    608
Absorbed variable: id                               No. of categories =     44
                                                    F(22, 43)         = 381.30
                                                    Prob > F          = 0.0000
                                                    R-squared         = 0.9800
                                                    Adj R-squared     = 0.9776
                                                    Root MSE          = 0.1290

                                    (Std. err. adjusted for 44 clusters in id)
------------------------------------------------------------------------------
             |               Robust
      lnpgdp | Coefficient  std. err.      t    P>|t|     [95% conf. interval]
-------------+----------------------------------------------------------------
         did |   .1612596   .0424702     3.80   0.000     .0756103    .2469089
      popden |   -2.83359   4.271172    -0.66   0.511    -11.44723    5.780049
         sav |   -.826351   .1212829    -6.81   0.000    -1.070941   -.5817607
    industry |    .123654   .0352388     3.51   0.001     .0525882    .1947198
    non_agri |  -1.220827   .3814877    -3.20   0.003    -1.990171   -.4514841
     welfare |  -.0013941   .0021004    -0.66   0.510      -.00563    .0028417
         fdi |  -.4705762   .6373817    -0.74   0.464    -1.755979    .8148265
         exp |   .1311563   .0920516     1.42   0.161    -.0544835     .316796
             |
        year |
       2003  |   .0867016   .0177547     4.88   0.000     .0508958    .1225074
       2004  |   .1497615   .0234327     6.39   0.000     .1025051     .197018
       2005  |   .2401505   .0370452     6.48   0.000     .1654417    .3148593
       2006  |    .285288   .0475912     5.99   0.000     .1893112    .3812649
       2007  |   .4044815   .0519725     7.78   0.000      .299669    .5092939
       2008  |    .618554    .064974     9.52   0.000     .4875215    .7495865
       2009  |   .7602133   .0720347    10.55   0.000     .6149415    .9054851
       2010  |   .9474614   .0787456    12.03   0.000     .7886558    1.106267
       2011  |    1.12886   .0840711    13.43   0.000     .9593141    1.298405
       2012  |   1.230967   .0942061    13.07   0.000     1.040982    1.420952
       2013  |   1.302292   .1021949    12.74   0.000     1.096196    1.508387
       2014  |   1.283281    .116348    11.03   0.000     1.048643    1.517919
       2015  |   1.397266   .1128194    12.38   0.000     1.169744    1.624788
       2016  |   1.489624   .1268996    11.74   0.000     1.233706    1.745541
             |
       _cons |   8.772451   .4469524    19.63   0.000     7.871086    9.673816
------------------------------------------------------------------------------

二、双重差分模型DID的检验

2.1DID的三个前提假设

①共同趋势假设（DID不要求随机分组，只要外生即可；处理组和对照组在政策实施之前必须有共同的变化趋势）

②政策外生性假定（个体在政策生效前不能对未来政策是否实施产生预期，否则会干扰政策实施效果）即：did可以与ui有关系，但不可以与误差项eit有相关关系）

③非观测性因素的影响（1.个体无法预估政策实施时间，2.个体变换不受同时期其他政策的影响）

2.2平行趋势检验（动态效应检验）

· 该假设的重要性：共同趋势假设是DID的重要前提，若违背了该假设，则使用差分法也无法消除时间趋势项，使得估计得到的结果不一致，从而失去实际含义。

· 检验方法：

法一：画图（精度很低，不推荐，仅可作为辅助使用）

法二：动态效应检验

动态效应检验实质：引入有限个时间虚拟变量，并将其与处理组虚拟变量交乘，考察政策实施前后交乘项的显著性。动态效应检验和平行趋势检验是有区别的，平行趋势检验中，只要考察0时期前的交乘项是否显著，如果不显著，说明处理组和控制组在事前并没有显著差异，可以使用DID。

【如果满足动态和平行趋势检验，理想的情况应当是在政策实施前，交互项回归系数不显著；在政策实施后，回归系数显著且应当异于0；若只是平行趋势检验，则只要求政策实施前不显著，实施后显不显著不影响。】

参考文章：双重差分法之平行趋势检验_KEMOSABEr的博客-CSDN博客_平行趋势检验

注：在进行平行趋势检验时，一般会设政策实施当年为基期（即0期），观察前后的系数变化。（回归方程由于多重共线性，一定会有一个年份的系数被omitted，因为平行趋势检验重点关注政策实施前后的系数变换，则此处相当于手动设定omitted掉政策实施当年的系数） 

//平行趋势检验
*忽略掉13年当年的系数
*政策生效前05-12 8个时期和处理组的交互项
forvalues i=8(-1) 1{
	gen pre_`i'= ( year == 2013-`i' & treatment== 1)
}
*政策生效后14-16 3个时期和处理组的交互项
forvalues j=1(1) 3{
	gen post_`j'= ( year == 2013+`j' & treatment== 1)
} 

//建立新的含交互项的模型（动态效应检验）
*此处选用了普通的标准误（但我不知道为什么）
areg lnpgdp pre_* post_* $cv i.year,absorb(id)

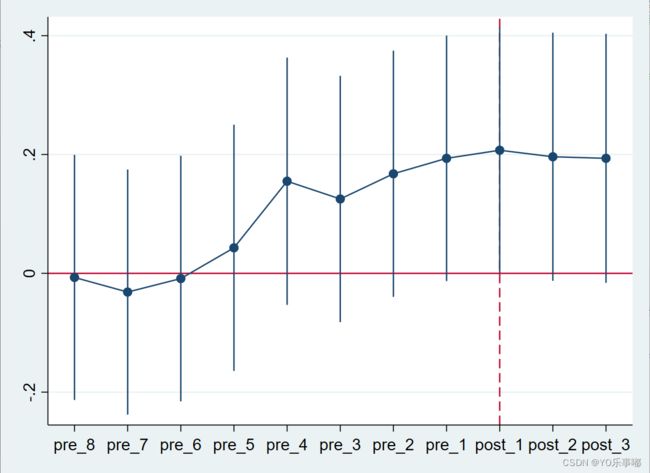
//将平行趋势检验结果绘图
//ssc install coefplot 
coefplot,keep(pre_* post_*) vertical recast(connect) yline(0) xline(9,lp(dash))

回归结果显示：通过了平行趋势检验，在政策实施前，pre8-pre5的回归系数在5%显著水平下无法通过检验，是不显著的，在政策实施后pre4-pre0的系数在10%检验水平下显著。此时可以认为符合共同趋势假设。

延申：关于回归系数与其置信区间绘图的命令coefplot

参考文章：https://zhuanlan.zhihu.com/p/489077475?utm_id=0

2.3政策外生性检验

检验政策外生性假定（待补充）

2.4安慰剂检验

检验：其他遗漏的非观测性因素的影响。

两种情况：a.虚构政策实施时间 b.虚构处理组；

关于政策实施时间：如果怀疑个体可以提前预估政策实施时间，则使用法a：在虚构了不同政策实施时间后，若结果仍然普遍显著，则不通过检验；若估计结果不显著或是在0附近，则认为个体无法预测政策实施时间，通过了安慰剂检验。

关于处理组：（1）怀疑两组的变换还受到了同时期，未被控制到的其他政策的影响；(2) 或是认为个体可以预知自己是否被执行政策，则使用法b：若重复虚拟分组后，回归结果普遍不好，则认为通过了安慰剂检验，政策是外生的。

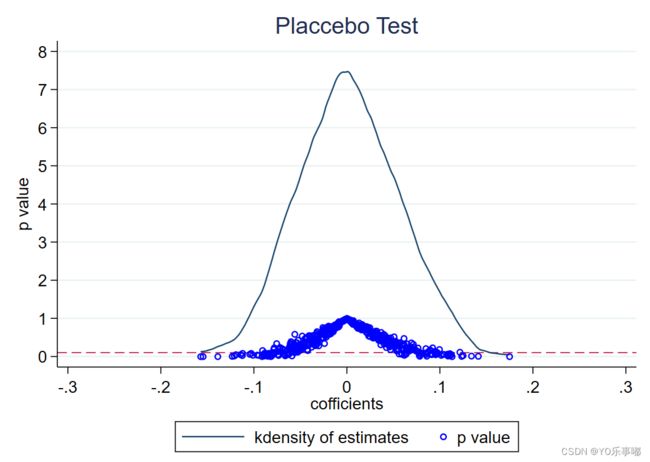
虚构处理组：在样本中随机选取与初始处理组和控制组数量一致的样本，进行DID建模。该随机过程重复进行n次（n通常取200-500），得到的核心解释变量系数的估计结果绘制出密度曲线，若其结果集中在0附近，且不显著，则认为分组结果的效果并不好，因而证明了政策是外生的，可以忽略其他政策和随机性因素的影响。

本题进行安慰剂检验绘图结果如下，显然估计的系数普遍在0附近波动，通过了该假设检验。

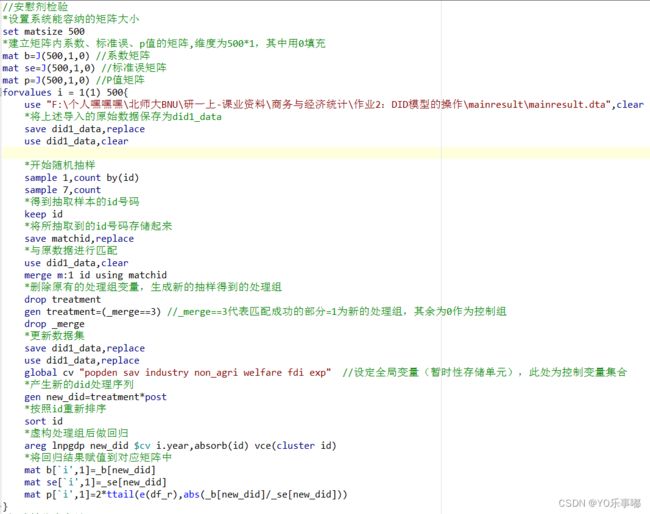
代码：【较为复杂】

第一步：建立一个虚构处理组的循环，重复进行n次，将得到的估计结果放到矩阵当中

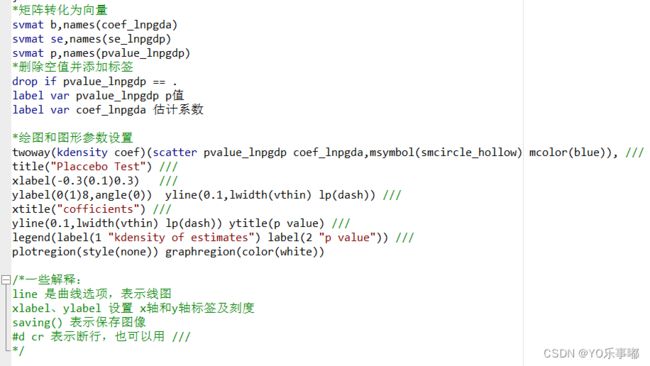
 第二步：将上一步的系数估计结果绘图

三.实证过程

step1：准备工作

use "F:\个人嘿嘿嘿\北师大BNU\研一上-课业资料\商务与经济统计\作业2：DID模型的操作\mainresult\mainresult.dta",clear
sum id year treatment post did lnpgdp //核心变量的描述性统计

//设定全局变量（暂时性存储单元），此处为控制变量集合
global cv "popden sav industry non_agri welfare fdi exp"  
xtset id year //设定面板模型的时间和个体

step2：基础DID模型的两种命令形式

//DID模型
reg lnpgdp did $cv i.id i.year,vce(cluster id) //$cv为使用设定的全局变量
areg lnpgdp did $cv i.year,absorb(id) vce(cluster id) 

step3：平行趋势检验

//平行趋势检验
*政策生效前05-12 8个时期和处理组的交互项
forvalues i=8(-1) 1{
	gen pre_`i'= ( year == 2013-`i' & treatment== 1)
}
*政策生效后14-16 3个时期和处理组的交互项
forvalues j=1(1) 3{
	gen post_`j'= ( year == 2013+`j' & treatment== 1)
} 
areg lnpgdp pre_* post_* $cv i.year,absorb(id) vce(cluster id)
areg lnpgdp pre_* post_* $cv i.year,absorb(id)
//ssc install coefplot 
coefplot,keep(pre_* post_*) vertical recast(connect) yline(0) xline(9,lp(dash))

step4：安慰剂检验

//安慰剂检验
*设置系统能容纳的矩阵大小
set matsize 500
*建立矩阵内系数、标准误、p值的矩阵,维度为500*1，其中用0填充
mat b=J(500,1,0) //系数矩阵
mat se=J(500,1,0) //标准误矩阵
mat p=J(500,1,0) //P值矩阵

*建立循环
forvalues i = 1(1) 500{
    *以下部分较为繁琐可以省去
	use "F:\个人嘿嘿嘿\北师大BNU\研一上-课业资料\商务与经济统计\作业2：DID模型的操作\mainresult\mainresult.dta",clear
	*将上述导入的原始数据保存为did1_data
	save did1_data,replace
	*使用以上数据
	use did1_data,clear
	
	*开始随机抽样（此处有一些疑问）
	sample 1,count by(id)
	sample 7,count
	*得到抽取样本的id号码
	keep id
	*将所抽取到的id号码存储起来
	save matchid,replace
	*与原数据进行匹配
	use did1_data,clear
	merge m:1 id using matchid
	*删除原有的处理组变量，生成新的抽样得到的处理组
	drop treatment
	gen treatment=(_merge==3) //_merge==3代表匹配成功的部分=1为新的处理组，其余为0作为控制组
	drop _merge
	*更新数据集
	save did1_data,replace
	use did1_data,replace
	global cv "popden sav industry non_agri welfare fdi exp"  //设定全局变量（暂时性存储单元），此处为控制变量集合
	*产生新的did处理序列
	gen new_did=treatment*post
	*按照id重新排序
	sort id
	*虚构处理组后做回归
	areg lnpgdp new_did $cv i.year,absorb(id) vce(cluster id)
	*将回归结果赋值到对应矩阵中
	mat b[`i',1]=_b[new_did]
	mat se[`i',1]=_se[new_did]
	mat p[`i',1]=2*ttail(e(df_r),abs(_b[new_did]/_se[new_did]))
}

*矩阵转化为向量
svmat b,names(coef_lnpgda)
svmat se,names(se_lnpgdp)
svmat p,names(pvalue_lnpgdp)
*删除空值并添加标签
drop if pvalue_lnpgdp == .
label var pvalue_lnpgdp p值
label var coef_lnpgda 估计系数

*绘图和图形参数设置
twoway(kdensity coef)(scatter pvalue_lnpgdp coef_lnpgda,msymbol(smcircle_hollow) mcolor(blue)), ///
title("Placcebo Test") ///
xlabel(-0.3(0.1)0.3)   ///
ylabel(0(1)8,angle(0))  yline(0.1,lwidth(vthin) lp(dash)) ///
xtitle("cofficients") ///
yline(0.1,lwidth(vthin) lp(dash)) ytitle(p value) ///
legend(label(1 "kdensity of estimates") label(2 "p value")) ///
plotregion(style(none)) graphregion(color(white))

/*一些解释：
line 是曲线选项，表示线图
xlabel、ylabel 设置 x轴和y轴标签及刻度  
saving() 表示保存图像
#d cr 表示断行，也可以用 /// 
*/