ccc-sklearn-16-XGBoost(2)
文章目录
-
-
-
- XGBoost的其他参数
-
- 选择弱评估器:参数booster
- XGB的目标函数:参数objective
-
- XGB目标函数的求解
- 参数化决策树 f t f_t ft:参数alpha,lambda
-
- 寻找最佳树结构:求解w和T
- 寻找最佳分枝:结构分数之差
- 让树停止生长:重要参数gamma
-
-
XGBoost的其他参数
选择弱评估器:参数booster
XGB中除了树模型还可以选择线性模型等其他模型
| xgb.train() & params | xgb.XGBRegressor() |
|---|---|
| xgb_model | booster |
| 使用哪种弱评估器。可以输入gbtree,gblinear或dart。输入的评估器不同,使用的params参数也不同,每种评估器都有自己的params列表。评估器必须于param参数相匹配,否则报错。 | 使用哪种弱评估器。可以输入gbtree,gblinear或dartgbtree代表梯度提升树,dart是Dropouts meet MultipleAdditive Regression Trees,可译为抛弃提升树,在建树的过程中会抛弃一部分树,比梯度提升树有更好的防过拟合功能。输入gblinear使用线性模型 |
不同弱评估器在波士顿房价数据集的表现:
for booster in ["gbtree","gblinear","dart"]:
reg = XGBR(n_estimators=180,
learning_rate=0.1,
random_state=420,
booster=booster).fit(Xtrain,Ytrain)
print(booster)
print(reg.score(Xtest,Ytest))
XGB的目标函数:参数objective
XGB的目标函数写作:
O b j = ∑ i = 1 m l ( y i , y ^ i ) + ∑ k = 1 K Ω ( f k ) Obj=\sum_{i=1}^{m}l(y_i,\hat y_i)+\sum_{k=1}^{K}\Omega(f_k) Obj=i=1∑ml(yi,y^i)+k=1∑KΩ(fk)
其中i表示数据集中的第i个样本,m表示导入第k棵树的数据总量,K代表建立的所有树。l为损失函数,通常是RMSE,调节后的均方误差。第二项代表模型的复杂度,使用树模型的某种变换。迭代每一颗树过程中,都最小化Obj来获取最优的 y ^ \hat y y^,同时最小化模型的错误率和复杂度。

方差是模型在不同数据集上表现出来的稳定性,偏差是模型预测的准确度。XGBoost的损失函数中自带限制方差变大的部分,不会轻易落到图像的右上方。下面是实际应用的选择:
| xgb.train() | xgb.XGBRegressor() | xgb.XGBClassifier() |
|---|---|---|
| obj:默认binary:logistic | objective:默认reg:linear | objective:默认binary:logistic |
常用选择:
| 输入 | 选用的损失函数 |
|---|---|
| reg:linear | 使用线性回归的损失函数,均方误差,回归时使用 |
| binary:logistic | 使用逻辑回归的损失函数,对数损失log_loss,二分类时使用 |
| binary:hinge | 使用支持向量机的损失函数,Hinge Loss,二分类时使用 |
| multi:softmax | 使用softmax损失函数,多分类时使用 |
| - | 还可以自己定义损失函数 |
xgboost库与sklearn对比
#sklearn
reg = XGBR(n_estimators=180,random_state=420).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)
MSE(Ytest,reg.predict(Xtest))
#XGboost库
import xgboost as xgb
dtrain = xgb.DMatrix(Xtrain,Ytrain)
dtest = xgb.DMatrix(Xtest,Ytest)
dtrain
#无法打开查看,通常先pandas读再放到DMatrix中
param = {'verbosity':0, #最新的xgboost已经移除了silent 替换成verbosity
'objective':'reg:linear',
'eta':0.1}
num_round = 180
bst = xgb.train(param,dtrain,num_round)
from sklearn.metrics import r2_score
r2_score(Ytest,bst.predict(dtest))
MSE(Ytest,bst.predict(dtest))

可以看到,从 R 2 R^2 R2还是MSE的角度,都是xgb库本身表现更加优秀。这与其作者陈天奇的论文结论也是相符的,差异可能与底层代码编写有关
XGB目标函数的求解
求解的目的是将目标函数转化成更简单的,与树的结构直接相关的写法。建立树的结构与模型的效果之间的直接联系。转换过程如下:

g i g_i gi和 h i h_i hi分别是损失函数求导的一阶导和二阶导,统称为每个样本的梯度统计量。当有许多树的时候,目标函数转换成:
O b j = ∑ i = 1 m [ f t ( x i ) g i + 1 2 ( f t ( x i ) ) 2 h i ] + Ω ( f t ) Obj=\sum_{i=1}^{m}[f_t(x_i)g_i+\frac{1}{2}(f_t(x_i))^2h_i]+\Omega(f_t) Obj=i=1∑m[ft(xi)gi+21(ft(xi))2hi]+Ω(ft)
g i g_i gi和 h i h_i hi只与传统损失函数相关,核心是需要决定的 f t f_t ft,也是下一个参数的研究对象
参数化决策树 f t f_t ft:参数alpha,lambda
XGB中每个叶子结点上都有一个预测分数,也被称为叶子权重

叶子权重就是所有在叶子结点上样本的回归取值,多棵树时集成模型的回归结果就是所有树的预测分数之和。整个模型在样本i上给出的预测结果为:
y ^ i ( k ) = ∑ k K f k ( x i ) \hat y_i^{(k)}=\sum_{k}^{K}f_k(x_i) y^i(k)=k∑Kfk(xi)
K表示模型中共有K颗树, f k ( x i ) f_k(x_i) fk(xi)表示叶子,形象表示如下:

某颗树的某个叶子结点上的所有样本对应叶子权重相同,设一棵树上包含T个叶子结点,叶子结点的索引为j,结点上样本权重 w j w_j wj。可以定义模型复杂度为:
Ω ( f ) = γ T + R e g u l a r i z a t i o n \Omega(f)=\gamma T+Regularization Ω(f)=γT+Regularization

由于XGboost中所有树都是二叉树,所以可以使用T来判断树的结构。参数 α \alpha α 和 λ \lambda λ用于控制正则化强度,都为0时表示普通梯度提升树的目标函数。对应参数如下:
| 参数含义 | xgb.train() | xgb.XGBRegressor() |
|---|---|---|
| L1正则项的参数 | alpha,默认0,取值范围[0, +∞] | reg_alpha,默认0,取值范围[0, +∞] |
| L2正则项的参数 | lambda,默认1,取值范围[0, +∞] | reg_lambda,默认1,取值范围[0, +∞] |
对于树模型,剪枝参数的地位更高,参数alpha和lambda一般使用用网格搜索调整即可
寻找最佳树结构:求解w和T
假设第t棵树已确定为q,可以将树的结构代入损失函数,继续转化目标函数。使用默认的L2正则化可以推导如下:

文字框转化过程如下:

对于最终的式子,定义:
G j = ∑ i ∈ I j g i , H j = ∑ i ∈ I j h i G_j=\sum_{i\in I_j}g_i,H_j=\sum_{i\in I_j}h_i Gj=i∈Ij∑gi,Hj=i∈Ij∑hi
可以得到:
O b j ( t ) = ∑ j = 1 T [ w j G j + 1 2 w j 2 ( H j + λ ) ] + γ T Obj^{(t)}=\sum_{j=1}^{T}[w_jG_j+\frac{1}{2}w_j^2(H_j+\lambda)]+\gamma T Obj(t)=j=1∑T[wjGj+21wj2(Hj+λ)]+γT
每个j取值下都当作第一项为一个二次函数 F ∗ F^* F∗,目标是追求Obj最小,只要单独的每一个叶子j取值下的二次函数都最小即可。于是对其求导可得:
∂ F ∗ ( w j ) ∂ w j = G j + w j ( H j + λ ) w j = − G j H j + λ \frac{\partial F^*(w_j)}{\partial w_j}=G_j+w_j(H_j+\lambda) \\ w_j=-\frac{G_j}{H_j+\lambda} ∂wj∂F∗(wj)=Gj+wj(Hj+λ)wj=−Hj+λGj
将公式代入目标函数有:

此时目标函数可以称作结构分数,分数越低则树整体结构越好,形象表示如下:

O b j = − ( g 1 2 h 1 + λ + g 4 2 h 4 + λ + ( g 2 + g 3 + g 5 ) 2 h 2 + h 3 + h 5 + λ + 3 γ ) Obj=-(\frac{g_1^2}{h_1+\lambda}+\frac{g_4^2}{h_4+\lambda}+\frac{(g_2+g_3+g_5)^2}{h_2+h_3+h_5+\lambda}+3\gamma) Obj=−(h1+λg12+h4+λg42+h2+h3+h5+λ(g2+g3+g5)2+3γ)
求解Obj的其实就是求解树的结构(T)。可以通过枚举所有可能的树结构q,然后一个个计算Obj来选定最佳树结构完成迭代。此时将使用贪婪算法寻找最佳结构
寻找最佳分枝:结构分数之差
贪婪算法值控制局部最优来达到全局最优, 类似于决策树生长过程,XGBoost中生成树结构如下:

举个例子:

对于中间的叶子结点,计算分枝后的分数之差为:
G a i n = S c o r e s i s + S c o r e b r o − S c o r e m i d d l e = − 1 2 g 4 2 h 4 + λ + γ − 1 2 g 1 2 h 1 + λ + γ + 1 2 G 2 H + λ − γ = − 1 2 [ g 4 2 h 4 + λ + g 1 2 h 1 + λ − ( g 1 + g 4 ) 2 h 1 + h 4 + λ ] + γ Gain = Score_{sis}+Score_{bro}-Score_{middle} \\=-\frac{1}{2}\frac{g_4^2}{h_4+\lambda}+\gamma-\frac{1}{2}\frac{g_1^2}{h_1+\lambda}+\gamma+\frac{1}{2}\frac{G^2}{H+\lambda}-\gamma\\=-\frac{1}{2}[\frac{g_4^2}{h_4+\lambda}+\frac{g_1^2}{h_1+\lambda}-\frac{(g_1+g_4)2}{h_1+h_4+\lambda}]+\gamma Gain=Scoresis+Scorebro−Scoremiddle=−21h4+λg42+γ−21h1+λg12+γ+21H+λG2−γ=−21[h4+λg42+h1+λg12−h1+h4+λ(g1+g4)2]+γ
由于CART树都是二叉树,进行推广可以总结出分枝结构差:
G a i n = 1 2 [ G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ ] − γ Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)2}{H_L+H_R+\lambda}]-\gamma Gain=21[HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2]−γ
这个公式可以对任意分枝计算,而且实践证明它比原始梯度下降速度更快,表现也不错
让树停止生长:重要参数gamma
XGB中规定,只要结构分数之差Gain大于0,即只要目标函数还能减小就允许继续分枝。表示如下:
1 2 [ G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ ] > γ \frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)2}{H_L+H_R+\lambda}]>\gamma 21[HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2]>γ
gamma这里定义为进一步分枝所需要的最小目标函数的减少量,在决策树。设置越大算法就越保守,树的叶子数量就越少,模型复杂度就越低:
| 参数含义 | xgb.train() | xgb.XGBRegressor() |
|---|---|---|
| 复杂度的惩罚项 γ \gamma γ | gamma,默认0,取值范围[0, +∞] | gamma,默认0,取值范围[0, +∞] |
学习曲线绘制体现gamma作用
axisx = np.arange(0,5,0.05)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=180,random_state=420,gamma=i)
result = CVS(reg,Xtrain,Ytrain,cv=cv)
rs.append(result.mean())
var.append(result.var())
ge.append((1-result.mean())**2+result.var())
print(axisx[rs.index(max(rs))].max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)*0.1
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()
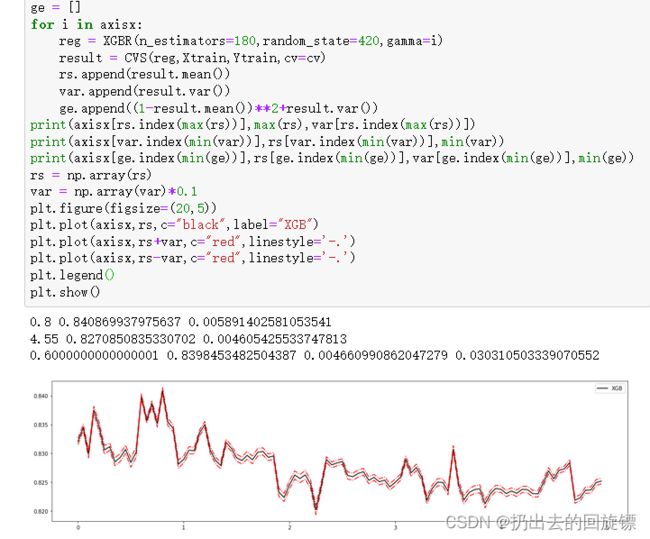
遗憾的是,这个图像似乎没有什么可靠的规律。这是由于sklearn中XGBoost不稳定,一般调整gamma可以选择xgboost库中的cv

import xgboost as xgb
dfull = xgb.DMatrix(X,y)
param1 = {'silent':True,'obj':'reg:linear',"gamma":0}
num_round = 180
n_fold=5
time0 = time()
cvresult1 = xgb.cv(param1,dfull,num_round,n_fold)
print(datetime.datetime.fromtimestamp(time()-time0,pytz.timezone('UTC')).strftime("%M:%S:%f"))
plt.figure(figsize=(20,5))
plt.grid()
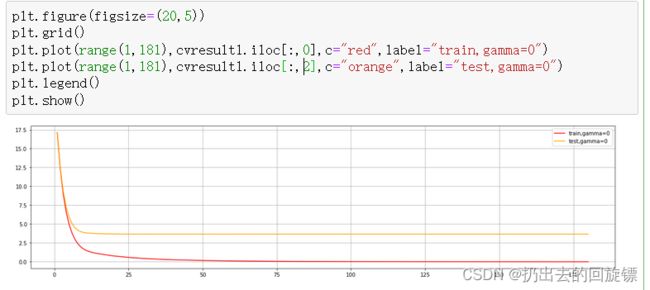
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.legend()
plt.show()
| 指标 | 含义 |
|---|---|
| rmse | 回归用,调整后的均方误差 |
| mae | 回归用,绝对平均误差 |
| logloss | 二分类用,对数损失 |
| mlogloss | 多分类用,对数损失 |
| error | 分类用,分类误差,等于1-准确率 |
| auc | 分类用,AUC面积 |
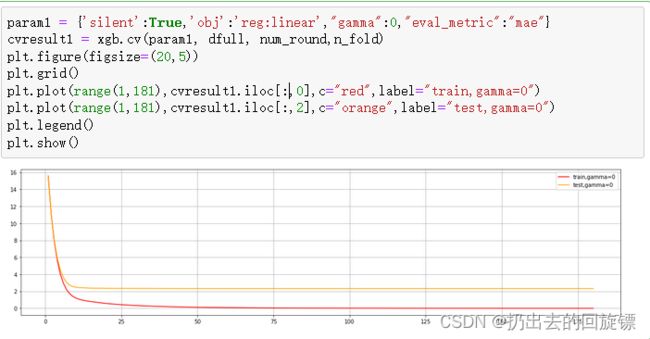
回归案例使用绝对平均误差
param1 = {'silent':True,'obj':'reg:linear',"gamma":0,"eval_metric":"mae"}
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.legend()
plt.show()
param1 = {'silent':True,'obj':'reg:linear',"gamma":0}
param2 = {'silent':True,'obj':'reg:linear',"gamma":20}
num_round = 180
n_fold=5
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)
cvresult2 = xgb.cv(param2, dfull, num_round,n_fold)
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.plot(range(1,181),cvresult2.iloc[:,0],c="green",label="train,gamma=20")
plt.plot(range(1,181),cvresult2.iloc[:,2],c="blue",label="test,gamma=20")
plt.legend()
plt.show()

增大gamma在测试集效果相同的情况下削弱了测试集效果,减少过拟合现象
分类例子:
from sklearn.datasets import load_breast_cancer
data2 = load_breast_cancer()
x2 = data2.data
y2 = data2.target
dfull2 = xgb.DMatrix(x2,y2)
param1 = {'silent':True,'obj':'binary:logistic',"gamma":0,"nfold":5}
param2 = {'silent':True,'obj':'binary:logistic',"gamma":2,"nfold":5}
num_round = 100
cvresult1 = xgb.cv(param1, dfull2, num_round,metrics=("error"))
cvresult2 = xgb.cv(param2, dfull2, num_round,metrics=("error"))
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,101),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,101),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.plot(range(1,101),cvresult2.iloc[:,0],c="green",label="train,gamma=2")
plt.plot(range(1,101),cvresult2.iloc[:,2],c="blue",label="test,gamma=2")
plt.legend()
plt.show()