【旅行商问题】蚁群算法解决旅行商问题【Matlab】

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

一、旅行商问题

1、问题描述

旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。[1]

2、数学模型

旅行商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设有n个城市和距离矩阵D=[dij]，其中dij表示城市i到城市j的距离，i，j=1，2 … n，则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。

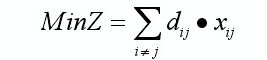
其中dij代表i点到j点的距离，xij取值为0或1，代表是否有次路径。问题的目标函数MinZ代表要使所有的路径长度之和最小。

二、蚁群算法

1、引言

Marco Dorigo等人在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标，于是在1991年在其博士论文中首次系统地提出一种基于蚂蚁种群的新型智能优化算法“蚂蚁系统（Ant system,简称AS）”，后来，提出者及许多研究者对该算法作了各种改进，将其应用于更为广泛的领域，如图着色问题、二次分配问题、工件排序问题、车辆路径问题、车间作业调度问题、网络路由问题、大规模集成电路设计等。近些年来，M.Dorigo等人把蚂蚁算法进一步发展成一种通用的优化技术“蚁群优化（Ant Colony Optimization,简称ACO）”，并将所有符合ACO框架的算法称为“蚁群优化算法（ACO algorithm）”。

2、蚁群算法求解TSP原理

1、设整个蚂蚁群体中蚂蚁的数量为m，城市的数量为n，城市i与城市j之间的距离为dij（i,j=1,2,3,…,n），t时刻城市i与城市j链接路径上的信息素浓度为xij。初始时刻，各个城市间连接路径上的信息素浓度相同且为0.
2、蚂蚁k（k=1,2,3,…,n）根据各个城市间连接路径上的信息素浓度决定其下一个访问城市，设Pkij(t)表示t时刻蚂蚁k从城市i转移到城市j的概率，其计算公式为：
其中nij(t)为启发函数，nij(t)=1/dij，表示蚂蚁从城市i转移到城市j的期望程度；allowk（k=1,2,…m）为蚂蚁k待访问城市的集合，开始时，allowk中有(n-1)哥元素，即包括除了蚂蚁k出发城市的其他所有城市，随着时间的推进，allowk中的元素不断减少，直至为空，即表示所有的城市均访问完毕；α为信息素重要程度因子，其值越大，表示信息素的浓度在转移中起的作用越大；β为启发函数重要程度因子，其值越大，表示启发函数在转移中起的作用越大，即蚂蚁会以较大的概率转移到距离短的城市。
3、在蚂蚁释放信息素的同时，各个城市间连接路径上的信息素逐渐消失，设参数ρ(o<ρ<1)表示信息素的挥发程度。因此，当所有蚂蚁完成一次循环后，各个城市间连接路径上的信息素浓度需要进行实时更新，即：

三、源代码

%% 清空环境变量
clear all;
clc;

%% 导入数据
data=load('eil51.txt');          
Citys=[data(:,2),data(:,3)];    %城市坐标

%% 计算城市间相互距离
N=size(Citys,1);
D=distance(Citys,N);

%% 初始化参数
m=50;                           %蚂蚁数量
Alpha=1;                        %信息素重要程度因子
Beta=5;                         %启发函数重要程度因子
Rho=0.1;                        %信息素挥发因子
Q=1;                            %常系数
Eta=1./D;                       %启发函数
Tau=ones(N,N);                  %信息素矩阵
Route=zeros(m,N);               %路径记录表
C_Iter=1;                       %迭代次数初值
M_Iter=200;                       %最大迭代次数
Route_best=zeros(M_Iter,N);     %各代最佳路径
Length_best=zeros(M_Iter,1);    %各代最佳路径的长度
Length_ave=zeros(M_Iter,1);     %各代路径的平均长度

%% 迭代寻找最佳路径
while C_Iter<=M_Iter
    Route=find_Route(m,N,Tau,Alpha,Beta,Eta);%获取路径
    fitness=get_Fit(Route,D);   %计算每条路径的距离
    % 计算最短路径及平均距离
    if C_Iter==1
        [min_Length,min_index]=min(fitness);
        Length_best(C_Iter)=min_Length;
        Route_best(C_Iter,:)=Route(min_index,:);
        Length_ave(C_Iter)=mean(fitness);
    else
        [min_Length,min_index]=min(fitness);
        Length_best(C_Iter)=min(Length_best(C_Iter-1),min_Length);
        Length_ave(C_Iter)=mean(fitness);
        if Length_best(C_Iter-1)>min_Length
            Route_best(C_Iter,:)=Route(min_index,:);
        else
            Route_best(C_Iter,:)=Route_best(C_Iter-1,:);
        end
    end
    Tau=get_Tau(N,Route,Q,fitness,Rho,Tau);
    % 迭代次数加1并清空路径表
    C_Iter=C_Iter+1;
    Route=zeros(m,N);

end

%% 结果显示
best_route=Route_best(end,:);
best_length=Length_best(end,:);
disp(['最短距离: ' num2str(best_length)]);
disp(['最短路径: ' num2str(best_route)]);
draw(Citys,best_route,best_length,M_Iter,Length_ave,Length_best);

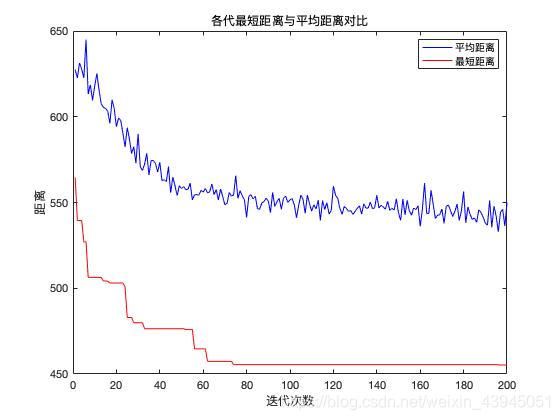
四、 结果展示

最短距离: 455.2612
最短路径: 18  47  12  46  51  27  48   8  26  31  28   3  20  35  36  22   1  32  11  38   5  49   9  50  16   2  29  21  34  30  10  39  33  45  15  44  37  17   4  41  19  42  40  13  25  14   6  23   7  43  24

五、备注

完整代码或代写添加QQ437651208

往期回顾>>>>>>
【选址问题】二进制灰狼算法解决无容量选址问题【Matlab】
【0-1背包】二进制灰狼算法解决0-1背包问题【Matlab】

[1]陈文兰, 戴树贵. 旅行商问题算法研究综述[J]. 滁州学院学报, 2006, 8(3):1-6.