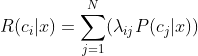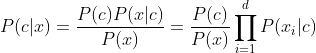- 机器学习数据预处理preprocessing之KernelCenterer
一叶_障目
机器学习人工智能
sklearn.preprocessing.KernelCenterer对矩阵XXX执行中心化操作,即使得核矩阵的行和列的均值为零给定二维矩阵XXX,可以下式得到其核变换矩阵KKK:K(X,X)=ϕ(X).ϕ(X)TK(X,X)=\phi(X).\phi(X)^TK(X,X)=ϕ(X).ϕ(X)T式中ϕ(X)\phi(X)ϕ(X)是一种将XXX从原始空间映射到希尔伯特空间的函数希尔伯特空间是一种完
- PyTorch机器学习与深度学习技术方法
Teacher.chenchong
机器学习python开发语言
近年来,随着AlphaGo、无人驾驶汽车、医学影像智慧辅助诊疗、ImageNet竞赛等热点事件的发生,人工智能迎来了新一轮的发展浪潮。尤其是深度学习技术,在许多行业都取得了颠覆性的成果。另外,近年来,Pytorch深度学习框架受到越来越多科研人员的关注和喜爱。Python基础知识串讲1、Python环境搭建(Python软件下载、安装与版本选择;PyCharm下载、安装;Python之HelloW
- 基于生成式人工智能的网联自动驾驶:通感融合决策技术
罗伯特之技术屋
行业信息处理技术与政策研究专栏人工智能自动驾驶机器学习
【摘要】探讨了生成式人工智能在网联自动驾驶技术中的潜在价值。现有研究主要侧重于传统感知决策和车联网技术,但却忽视了生成式人工智能在推动自动驾驶方面的重要作用。首先讨论了生成式人工智能技术如何提高自动驾驶决策、训练、感知和导航等模块的性能,接着探讨了其在融合了语义通信、通感一体和新型空口技术的下一代车联网中的角色,然后提出了基于人工智能代理的网联自动驾驶模型,最后强调生成式人工智能是实现车辆高级别自
- 人工智能英语学习笔记
「已注销」
基础篇单词mythologyn.ancientmythsingeneral;ideasthatmanypeoplethinkaretruebutthatdonotexistorarefalse神话Examples:AsatyrishalfmanandhalfgoatinGreekandRomanmythology.在希腊和罗马神话中,森林之神是半人半羊的样子。Thishasbeenwellillu
- 从小白到高手:人工智能学习中的挑战与突破
博雅智信
人工智能深度学习机器学习python大语言模型
引言:人工智能学习之路充满挑战学习过程中常见的问题与困境环境安装与配置问题简单报错反复调试,时间浪费大学习进度慢,难以找到合适的方向网上资料过多,选择困难导师催进度,任务压力大不敢多问:与同事、师兄师姐的尴尬理论与实践脱节,缺乏实战经验专注力不足,容易被干扰找一个师傅带着的好处高效解决问题,避免走弯路个性化学习路线与系统化知识框架实战经验的传授与导师的成长指导1.引言:人工智能学习之路充满挑战人工
- 文秘要学计算机吗,高考志愿:计算机专业和文秘专业哪个适合女生?
weixin_39707851
文秘要学计算机吗
原标题:高考志愿:计算机专业和文秘专业哪个适合女生?肯定是文秘专业更加适合女生吧,这对绝大部分女生来说是适用的。其实目前对高中毕业之后读大专的话,能够选择的热门专业不多。目前这个文秘类的专业,像这种速度方向的专业的话,还算是比较热门的。对于绝大部分大专生而言,尤其是女生而言是比较适合报考这种文秘类的专业的。因为目前来说像文秘类这种专业,社会上的需求比较大的。虽然目前有出现这种人工智能方面的软件,减
- 计算机专业毕业可以做文秘吗,高考志愿:计算机专业和文秘专业哪个适合女生?...
ShuYini
计算机专业毕业可以做文秘吗
原标题:高考志愿:计算机专业和文秘专业哪个适合女生?肯定是文秘专业更加适合女生吧,这对绝大部分女生来说是适用的。其实目前对高中毕业之后读大专的话,能够选择的热门专业不多。目前这个文秘类的专业,像这种速度方向的专业的话,还算是比较热门的。对于绝大部分大专生而言,尤其是女生而言是比较适合报考这种文秘类的专业的。因为目前来说像文秘类这种专业,社会上的需求比较大的。虽然目前有出现这种人工智能方面的软件,减
- 华为 Ascend 平台 YOLOv5 目标检测推理教程
Lunar*
目标检测华为YOLO目标检测
1.背景介绍随着人工智能技术的快速发展,目标检测在智能安防、自动驾驶、工业检测等领域中扮演了重要角色。YOLOv5是一种高效的目标检测模型,凭借其速度和精度的平衡广受欢迎。华为Ascend推理框架(ACL)是AscendCANN软件栈的核心组件,专为AscendAI加速硬件(如Atlas300I)设计,可实现高性能的深度学习推理。在本文中,我们将介绍如何基于华为AscendACL推理框架对YOLO
- 机器学习和深度学习的概念
你好呀我是裤裤
深度学习笔记机器学习深度学习人工智能
MachineLearning机器学习,可以看作是找一个函数。这个函数是人类找不到的,所以交给机器来找。DifferenttypesofFunctions**Regression:**函数的输出是一个数值forexample:**Classification:**给出选项,让机器去选择。forexample:检测一个邮件是不是垃圾文件,就可以通过这个来做。选项是两个:垃圾文件or非垃圾文件。下面,
- Python学习路线
Python_JC
python
Python是一门易学易用的编程语言,广泛应用于数据处理、Web开发、人工智能、自动化运维、游戏开发等领域。本篇文章将介绍Python的学习路线以及一些值得参考的书籍。Python学习路线Python的学习路线主要包括以下几个方面:掌握Python基础知识:了解变量、数据类型、表达式、流程控制、函数、模块等基础概念。学习Python面向对象编程:学习类、对象、继承、多态等面向对象编程的概念和技术。
- 【2025最新计算机毕业设计】基于SSM的旅游与自然保护平台【提供源码+答辩PPT+文档+项目部署】
万码堂源码
计算机毕设精品实战案例实战项目源码课程设计vue.js前端计算机毕业设计毕设项目springboot
作者简介:✌CSDN新星计划导师、Java领域优质创作者、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行前辈交流。✌主要内容:Java项目、Python项目、前端项目、PHP、ASP.NET、人工智能与大数据、单片机开发、物联网设计与开发设计、简历模板、学习资料、面试题库、技术互助、就业指导等。业务范围:免费功能设计、开题报告、任务书
- 【源码+文档】基于SpringBoot+Vue旅游网站系统【提供源码+答辩PPT+参考文档+项目部署】
万码堂源码
实战项目源码计算机毕设精品实战案例springbootvue.js旅游
作者简介:✌CSDN新星计划导师、Java领域优质创作者、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行前辈交流。✌主要内容:Java项目、Python项目、前端项目、PHP、ASP.NET、人工智能与大数据、单片机开发、物联网设计与开发设计、简历模板、学习资料、面试题库、技术互助、就业指导等。业务范围:免费功能设计、开题报告、任务书
- 人工智能领域单词:英文解释
周杰伦_Jay
人工智能深度学习神经网络中文分词全文检索
目录1、前言2、单词组1:15个3、单词组2:15个4、单词组3:15个5、单词组4:15个6、单词组5:15个1、前言亲爱的家人们,创作很不容易,若对您有帮助的话,请点赞收藏加关注哦,您的关注是我持续创作的动力,谢谢大家!有问题请私信或联系邮箱:
[email protected]、单词组1:15个1、人工智能(ArtificialIntelligence,AI):atechnologythatsi
- 华为CANN架构与Ascend C算子开发
z1931195
华为
CANN架构CANN(ComputeArchitectureforNeuralNetworks)是华为专为应对人工智能场景而推出的一种新型异构计算架构。在当前快速发展的AI技术背景下,CANN致力于提供一种高效且灵活的解决方案,以支持多种AI框架的应用。其设计不仅仅关注于上层应用的兼容性,同时也服务于底层AI处理器的优化和编程需求,发挥了承上启下的关键作用,成为华为昇腾AI处理器计算效率提升的核心
- Python AI教程之二十一:监督学习之支持向量机(SVM)算法
潜洋
人工智能Python中级支持向量机算法机器学习python
支持向量机(SVM)算法支持向量机(SVM)是一种功能强大的机器学习算法,广泛用于线性和非线性分类以及回归和异常值检测任务。SVM具有很强的适应性,适用于各种应用,例如文本分类、图像分类、垃圾邮件检测、笔迹识别、基因表达分析、人脸检测和异常检测。SVM特别有效,因为它们专注于寻找目标特征中不同类别之间的最大分离超平面,从而使其对二分类和多分类都具有鲁棒性。在本大纲中,我们将探讨支持向量机(SVM)
- 探索极致AI性能:昇腾NPU与PyTorch的完美融合 —— Ascend Extension for PyTorch
尤琦珺Bess
探索极致AI性能:昇腾NPU与PyTorch的完美融合——AscendExtensionforPyTorch去发现同类优质开源项目:https://gitcode.com/项目简介在人工智能领域,高效灵活的框架与强大的硬件加速器是实现先进算法的关键组合。AscendExtensionforPyTorch插件,即torch_npu,正是这样一个解决方案,它无缝对接PyTorch框架,将华为昇腾AI处
- 【Rust】——不安全Rust
Y小夜
Rust(官方文档重点总结)rust开发语言后端
博主现有专栏:C51单片机(STC89C516),c语言,c++,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux,基于HTML5的网页设计及应用,Rust(官方文档重点总结),jQuery,前端vue.js,Javaweb开发,Python机器学习等主页链接:Y小夜-CSDN博客目录不安全的超能力解引用裸指针调用不安全函数或方法创建不安全代码的安全抽象使用e
- 超简单|Python实现机器学习算法——KNN
birdcome
python机器学习KNN算法
超简单|Python实现机器学习算法——KNNKNN算法简介算法实现步骤如何用python实现KNN算法Scikit-learn算法库实现KNN分类器Sklearn建模流程KNN算法简介KNN算法(k近邻算法)是一种有监督分类算法,它的原理非常简单,下面以一个简单的例子引入。已知两种酒的标签:赤霞珠和黑皮诺,在这个情景中,我们对酒进行分类的依据是酒精浓度和颜色深度,如下图所示:红色代表赤霞珠,紫色
- 《盘古大模型——鸿蒙NEXT的智慧引擎》
人工智能深度学习
在当今科技飞速发展的时代,华为HarmonyOSNEXT的发布无疑是操作系统领域的一颗重磅炸弹,其将人工智能与操作系统深度融合,开启了智能新时代。而盘古大模型在其中发挥着至关重要的核心作用。赋予小艺智能助手超强能力在鸿蒙NEXT中,盘古大模型赋予了小艺智能助手更强的记忆、推理和规划能力,使其能够支持23类常用记忆类型,掌握万亿token的知识量。基于盘古大模型,小艺可以实现诸如将带有表格的图片转化
- 《AI 造梦:解锁虚拟场景与角色逼真丰富密码》
人工智能深度学习
在科技飞速发展的当下,生成式人工智能正以前所未有的态势席卷各个领域,尤其在构建虚拟世界方面,展现出令人惊叹的潜力。从沉浸式游戏世界到逼真的影视特效场景,从栩栩如生的虚拟偶像到互动性极强的虚拟角色,生成式人工智能正在改写我们对虚拟场景和角色的认知。今天,就让我们深入探寻如何利用这一前沿技术,创造出更加逼真且丰富的虚拟场景与角色。生成式AI技术基石生成式对抗网络(GANs)和变分自编码器(VAEs)是
- 《鸿蒙微内核与人工智能算法协同,开启智能系统新时代》
人工智能深度学习
在当今科技飞速发展的时代,鸿蒙系统以其独特的微内核架构和对人工智能算法的深度融合,正引领着操作系统智能化的新潮流。本文将深入探讨鸿蒙系统的微内核架构是如何与人工智能算法高效协同,从而提升系统性能和智能化水平的。鸿蒙系统微内核架构的优势鸿蒙系统采用微内核架构,将核心功能模块化,只保留最基本的进程管理、内存管理和通信机制等功能在内核中,而文件系统、网络协议等则作为独立的模块放在用户空间运行。这种架构使
- 《机器学习模型快速收敛的秘籍大揭秘》
人工智能深度学习
在机器学习的领域中,让模型快速收敛是众多从业者和研究者们共同追求的目标。因为快速收敛不仅能节省大量的时间和计算资源,还能使模型更快地投入实际应用,为我们带来更高的效率和价值。以下是一些实现机器学习模型快速收敛的方法。选择合适的优化器优化器在模型训练中起着至关重要的作用,它决定了模型参数的更新方式和步长。常见的优化器如Adam、RMSProp和Momentum等都有各自的特点和优势。Adam结合了M
- 《量子AI:突破量子比特稳定性与容错性的关键瓶颈》
人工智能深度学习机器学习
在量子计算的发展进程中,量子比特的稳定性和容错性问题一直是阻碍其走向广泛应用的关键障碍。量子AI作为前沿技术,正积极探索各种途径来攻克这些难题。量子纠错:守护量子比特的精准防线量子纠错是解决量子比特稳定性和容错性问题的核心技术之一。其原理是通过在量子比特之间建立量子纠错码,来检测和纠正量子比特在计算过程中发生的错误。比如谷歌量子人工智能实验室采用的“表面码”技术,通过构建物理量子比特的网格来编码逻
- 第78期 | GPTSecurity周报
aigcgpts
GPTSecurity是一个涵盖了前沿学术研究和实践经验分享的社区,集成了生成预训练Transformer(GPT)、人工智能生成内容(AIGC)以及大语言模型(LLM)等安全领域应用的知识。在这里,您可以找到关于GPT/AIGC/LLM最新的研究论文、博客文章、实用的工具和预设指令(Prompts)。现为了更好地知悉近一周的贡献内容,现总结如下。SecurityPapers1.ChatNVD:借
- 智算中心建设热潮涌动 AI服务器赋能加速
数据中心
在数字化浪潮汹涌的今天,人工智能新技术新发展日新月异。智算作为数字经济时代的新生产力,正逐步成为推动经济社会高质量发展的新引擎。智算中心:算力时代的“新基建”近年来,随着人工智能技术的迅猛发展和广泛应用,智能算力需求持续爆发,推动了智算中心的快速发展。2022年,随着国家“东数西算”工程启动,我国算力地图正式开始,形成八大枢纽、十大算力中心集群。据中国电信研究院发布的《智算产业发展研究报告(202
- 让创意在幻觉中肆虐: 认识Illusion Diffusion AI
程序员
人工智能新境界在不断发展的人工智能领域,一款非凡的新工具应运而生,它能将普通照片转化为绚丽的艺术品。敬请关注IllusionDiffusion,这是一个将现实与想象力完美融合的AI驱动平台,可创造出迷人的视错觉和超现实意境。AI算法的魔力所在IllusionDiffusion的核心是借助先进的AI模型,包括StableDiffusion和ControlNet,来解读用户输入的文本提示,并生成相应的
- 10 个免费的 AI 图片生成工具分享
程序员
原文:https://openaigptguide.com/ai-picture-generator/在人工智能(AI)图像生成技术的推动下,各类AI图片生成网站如雨后春笋般涌现,为我们的日常生活提供了丰富多彩的视觉体验。AI图片生成技术原理人工智能(AI)图片生成技术原理是通过计算机程序使用深度学习算法从大量的数据中学习特征,并根据特征创建新的图片。该技术可以模拟人类的绘画过程,学习输入图像的潜
- 【Cursor】揭秘Cursor:如何免费无限使用这款AI编程神器?
ChatGPT-千鑫
人工智能AI编程
在当今科技飞速发展的时代,人工智能编程工具层出不穷,其中Cursor凭借其卓越的功能和用户友好的体验,迅速在国际市场上引发了广泛关注。最近,该公司成功获得了OpenAI的6000万美元投资,进一步验证了其潜力和市场价值。那么,Cursor究竟具备怎样的强大能力?又该如何实现免费无限制使用呢?本文将为您揭开Cursor的神秘面纱,并提供详细的使用指南,助您轻松上手!Cursor的强大功能Cursor
- 【人工智能】人工智能的10大算法详解(优缺点+实际案例)
ChatGPT-千鑫
人工智能人工智能算法gpt-3AI编程gptcodemoss能用AI
人工智能(AI)是现代科技的重要领域,其中的算法是实现智能的核心。本文将介绍10种常见的人工智能算法,包括它们的原理、训练方法、优缺点及适用场景。1.线性回归(LinearRegression)模型原理线性回归用于建立自变量(特征)与因变量(目标)之间的线性关系。其目标是寻找最佳拟合直线,使得预测值与实际值之间的误差最小化。模型训练通过最小二乘法来最小化预测值与真实值之间的误差,得到线性回归方程的
- Cursor
一只爱笑的小燕子
ChatGPThtml5java开发语言
一、什么是Cursor官网:Cursor|BuildFastCursor是一个开源的AI编程编辑器。开源地址https://github.com/pricing目前在国内是可以不需要其他东西,可以直接访问的。而且目「下面是官方的介绍:」Cursor是一个为AI编程而做的编辑器。它还处于早期阶段,但现在Cursor可以帮助你做一些事情。编写:使用Copilot更聪明的人工智能生成10-100行代码比
- ViewController添加button按钮解析。(翻译)
张亚雄
c
<div class="it610-blog-content-contain" style="font-size: 14px"></div>// ViewController.m
// Reservation software
//
// Created by 张亚雄 on 15/6/2.
- mongoDB 简单的增删改查
开窍的石头
mongodb
在上一篇文章中我们已经讲了mongodb怎么安装和数据库/表的创建。在这里我们讲mongoDB的数据库操作
在mongo中对于不存在的表当你用db.表名 他会自动统计
下边用到的user是表明,db代表的是数据库
添加(insert):
- log4j配置
0624chenhong
log4j
1) 新建java项目
2) 导入jar包,项目右击,properties—java build path—libraries—Add External jar,加入log4j.jar包。
3) 新建一个类com.hand.Log4jTest
package com.hand;
import org.apache.log4j.Logger;
public class
- 多点触摸(图片缩放为例)
不懂事的小屁孩
多点触摸
多点触摸的事件跟单点是大同小异的,上个图片缩放的代码,供大家参考一下
import android.app.Activity;
import android.os.Bundle;
import android.view.MotionEvent;
import android.view.View;
import android.view.View.OnTouchListener
- 有关浏览器窗口宽度高度几个值的解析
换个号韩国红果果
JavaScripthtml
1 元素的 offsetWidth 包括border padding content 整体的宽度。
clientWidth 只包括内容区 padding 不包括border。
clientLeft = offsetWidth -clientWidth 即这个元素border的值
offsetLeft 若无已定位的包裹元素
- 数据库产品巡礼:IBM DB2概览
蓝儿唯美
db2
IBM DB2是一个支持了NoSQL功能的关系数据库管理系统,其包含了对XML,图像存储和Java脚本对象表示(JSON)的支持。DB2可被各种类型的企 业使用,它提供了一个数据平台,同时支持事务和分析操作,通过提供持续的数据流来保持事务工作流和分析操作的高效性。 DB2支持的操作系统
DB2可应用于以下三个主要的平台:
工作站,DB2可在Linus、Unix、Windo
- java笔记5
a-john
java
控制执行流程:
1,true和false
利用条件表达式的真或假来决定执行路径。例:(a==b)。它利用条件操作符“==”来判断a值是否等于b值,返回true或false。java不允许我们将一个数字作为布尔值使用,虽然这在C和C++里是允许的。如果想在布尔测试中使用一个非布尔值,那么首先必须用一个条件表达式将其转化成布尔值,例如if(a!=0)。
2,if-els
- Web开发常用手册汇总
aijuans
PHP
一门技术,如果没有好的参考手册指导,很难普及大众。这其实就是为什么很多技术,非常好,却得不到普遍运用的原因。
正如我们学习一门技术,过程大概是这个样子:
①我们日常工作中,遇到了问题,困难。寻找解决方案,即寻找新的技术;
②为什么要学习这门技术?这门技术是不是很好的解决了我们遇到的难题,困惑。这个问题,非常重要,我们不是为了学习技术而学习技术,而是为了更好的处理我们遇到的问题,才需要学习新的
- 今天帮助人解决的一个sql问题
asialee
sql
今天有个人问了一个问题,如下:
type AD value
A
- 意图对象传递数据
百合不是茶
android意图IntentBundle对象数据的传递
学习意图将数据传递给目标活动; 初学者需要好好研究的
1,将下面的代码添加到main.xml中
<?xml version="1.0" encoding="utf-8"?>
<LinearLayout xmlns:android="http:/
- oracle查询锁表解锁语句
bijian1013
oracleobjectsessionkill
一.查询锁定的表
如下语句,都可以查询锁定的表
语句一:
select a.sid,
a.serial#,
p.spid,
c.object_name,
b.session_id,
b.oracle_username,
b.os_user_name
from v$process p, v$s
- mac osx 10.10 下安装 mysql 5.6 二进制文件[tar.gz]
征客丶
mysqlosx
场景:在 mac osx 10.10 下安装 mysql 5.6 的二进制文件。
环境:mac osx 10.10、mysql 5.6 的二进制文件
步骤:[所有目录请从根“/”目录开始取,以免层级弄错导致找不到目录]
1、下载 mysql 5.6 的二进制文件,下载目录下面称之为 mysql5.6SourceDir;
下载地址:http://dev.mysql.com/downl
- 分布式系统与框架
bit1129
分布式
RPC框架 Dubbo
什么是Dubbo
Dubbo是一个分布式服务框架,致力于提供高性能和透明化的RPC远程服务调用方案,以及SOA服务治理方案。其核心部分包含: 远程通讯: 提供对多种基于长连接的NIO框架抽象封装,包括多种线程模型,序列化,以及“请求-响应”模式的信息交换方式。 集群容错: 提供基于接
- 那些令人蛋痛的专业术语
白糖_
springWebSSOIOC
spring
【控制反转(IOC)/依赖注入(DI)】:
由容器控制程序之间的关系,而非传统实现中,由程序代码直接操控。这也就是所谓“控制反转”的概念所在:控制权由应用代码中转到了外部容器,控制权的转移,是所谓反转。
简单的说:对象的创建又容器(比如spring容器)来执行,程序里不直接new对象。
Web
【单点登录(SSO)】:SSO的定义是在多个应用系统中,用户
- 《给大忙人看的java8》摘抄
braveCS
java8
函数式接口:只包含一个抽象方法的接口
lambda表达式:是一段可以传递的代码
你最好将一个lambda表达式想象成一个函数,而不是一个对象,并记住它可以被转换为一个函数式接口。
事实上,函数式接口的转换是你在Java中使用lambda表达式能做的唯一一件事。
方法引用:又是要传递给其他代码的操作已经有实现的方法了,这时可以使
- 编程之美-计算字符串的相似度
bylijinnan
java算法编程之美
public class StringDistance {
/**
* 编程之美 计算字符串的相似度
* 我们定义一套操作方法来把两个不相同的字符串变得相同,具体的操作方法为:
* 1.修改一个字符(如把“a”替换为“b”);
* 2.增加一个字符(如把“abdd”变为“aebdd”);
* 3.删除一个字符(如把“travelling”变为“trav
- 上传、下载压缩图片
chengxuyuancsdn
下载
/**
*
* @param uploadImage --本地路径(tomacat路径)
* @param serverDir --服务器路径
* @param imageType --文件或图片类型
* 此方法可以上传文件或图片.txt,.jpg,.gif等
*/
public void upload(String uploadImage,Str
- bellman-ford(贝尔曼-福特)算法
comsci
算法F#
Bellman-Ford算法(根据发明者 Richard Bellman 和 Lester Ford 命名)是求解单源最短路径问题的一种算法。单源点的最短路径问题是指:给定一个加权有向图G和源点s,对于图G中的任意一点v,求从s到v的最短路径。有时候这种算法也被称为 Moore-Bellman-Ford 算法,因为 Edward F. Moore zu 也为这个算法的发展做出了贡献。
与迪科
- oracle ASM中ASM_POWER_LIMIT参数
daizj
ASMoracleASM_POWER_LIMIT磁盘平衡
ASM_POWER_LIMIT
该初始化参数用于指定ASM例程平衡磁盘所用的最大权值,其数值范围为0~11,默认值为1。该初始化参数是动态参数,可以使用ALTER SESSION或ALTER SYSTEM命令进行修改。示例如下:
SQL>ALTER SESSION SET Asm_power_limit=2;
- 高级排序:快速排序
dieslrae
快速排序
public void quickSort(int[] array){
this.quickSort(array, 0, array.length - 1);
}
public void quickSort(int[] array,int left,int right){
if(right - left <= 0
- C语言学习六指针_何谓变量的地址 一个指针变量到底占几个字节
dcj3sjt126com
C语言
# include <stdio.h>
int main(void)
{
/*
1、一个变量的地址只用第一个字节表示
2、虽然他只使用了第一个字节表示,但是他本身指针变量类型就可以确定出他指向的指针变量占几个字节了
3、他都只存了第一个字节地址,为什么只需要存一个字节的地址,却占了4个字节,虽然只有一个字节,
但是这些字节比较多,所以编号就比较大,
- phpize使用方法
dcj3sjt126com
PHP
phpize是用来扩展php扩展模块的,通过phpize可以建立php的外挂模块,下面介绍一个它的使用方法,需要的朋友可以参考下
安装(fastcgi模式)的时候,常常有这样一句命令:
代码如下:
/usr/local/webserver/php/bin/phpize
一、phpize是干嘛的?
phpize是什么?
phpize是用来扩展php扩展模块的,通过phpi
- Java虚拟机学习 - 对象引用强度
shuizhaosi888
JAVA虚拟机
本文原文链接:http://blog.csdn.net/java2000_wl/article/details/8090276 转载请注明出处!
无论是通过计数算法判断对象的引用数量,还是通过根搜索算法判断对象引用链是否可达,判定对象是否存活都与“引用”相关。
引用主要分为 :强引用(Strong Reference)、软引用(Soft Reference)、弱引用(Wea
- .NET Framework 3.5 Service Pack 1(完整软件包)下载地址
happyqing
.net下载framework
Microsoft .NET Framework 3.5 Service Pack 1(完整软件包)
http://www.microsoft.com/zh-cn/download/details.aspx?id=25150
Microsoft .NET Framework 3.5 Service Pack 1 是一个累积更新,包含很多基于 .NET Framewo
- JAVA定时器的使用
jingjing0907
javatimer线程定时器
1、在应用开发中,经常需要一些周期性的操作,比如每5分钟执行某一操作等。
对于这样的操作最方便、高效的实现方式就是使用java.util.Timer工具类。
privatejava.util.Timer timer;
timer = newTimer(true);
timer.schedule(
newjava.util.TimerTask() { public void run()
- Webbench
流浪鱼
webbench
首页下载地址 http://home.tiscali.cz/~cz210552/webbench.html
Webbench是知名的网站压力测试工具,它是由Lionbridge公司(http://www.lionbridge.com)开发。
Webbench能测试处在相同硬件上,不同服务的性能以及不同硬件上同一个服务的运行状况。webbench的标准测试可以向我们展示服务器的两项内容:每秒钟相
- 第11章 动画效果(中)
onestopweb
动画
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- windows下制作bat启动脚本.
sanyecao2314
javacmd脚本bat
java -classpath C:\dwjj\commons-dbcp.jar;C:\dwjj\commons-pool.jar;C:\dwjj\log4j-1.2.16.jar;C:\dwjj\poi-3.9-20121203.jar;C:\dwjj\sqljdbc4.jar;C:\dwjj\voucherimp.jar com.citsamex.core.startup.MainStart
- Java进行RSA加解密的例子
tomcat_oracle
java
加密是保证数据安全的手段之一。加密是将纯文本数据转换为难以理解的密文;解密是将密文转换回纯文本。 数据的加解密属于密码学的范畴。通常,加密和解密都需要使用一些秘密信息,这些秘密信息叫做密钥,将纯文本转为密文或者转回的时候都要用到这些密钥。 对称加密指的是发送者和接收者共用同一个密钥的加解密方法。 非对称加密(又称公钥加密)指的是需要一个私有密钥一个公开密钥,两个不同的密钥的
- Android_ViewStub
阿尔萨斯
ViewStub
public final class ViewStub extends View
java.lang.Object
android.view.View
android.view.ViewStub
类摘要: ViewStub 是一个隐藏的,不占用内存空间的视图对象,它可以在运行时延迟加载布局资源文件。当 ViewSt
![]() 的定义,有如下公式表示:
的定义,有如下公式表示:![]() 被分类成
被分类成![]() 的条件风险,而
的条件风险,而![]() 表示真实标记为
表示真实标记为![]() 的输入样本
的输入样本![]() 被误分类成
被误分类成![]() 的损失,
的损失,![]() 表示后验概率,
表示后验概率,![]() 是输入样本总数。那么贝叶斯分类器的优化目标就是使条件风险最小化。
是输入样本总数。那么贝叶斯分类器的优化目标就是使条件风险最小化。![]() 即是机器学习模型需要学习到的东西。一般来说,这里有两种获取模式。第一种是判别式模型直接得到(BP神经网络、SVM。具体获取方法之后再补)。而对于生成式模型,通过我们概率论中的贝叶斯定理,可以将后验概率的获取转为如下公式:
即是机器学习模型需要学习到的东西。一般来说,这里有两种获取模式。第一种是判别式模型直接得到(BP神经网络、SVM。具体获取方法之后再补)。而对于生成式模型,通过我们概率论中的贝叶斯定理,可以将后验概率的获取转为如下公式:![]() 是先验概率(prior),就是不管输入如何,我只统计我最后分类结果出现的概率情况,
是先验概率(prior),就是不管输入如何,我只统计我最后分类结果出现的概率情况,![]() 和标签类别无关,所以我们在计算的时候不需要考虑,那么我们重点关注的便是似然概率
和标签类别无关,所以我们在计算的时候不需要考虑,那么我们重点关注的便是似然概率![]() (likelihood)。
(likelihood)。![]() 具有确定的形式并且被参数向量
具有确定的形式并且被参数向量![]() ,那么我们训练模型的目标就是基于训练集优化找到最优参数
,那么我们训练模型的目标就是基于训练集优化找到最优参数![]() 。
。![]() 表示训练集
表示训练集![]() 中属于第
中属于第![]() 类样本组成的集合,假设这些样本是独立同分布的,那么参数
类样本组成的集合,假设这些样本是独立同分布的,那么参数![]() 对于数据集
对于数据集![]() 的似然是:
的似然是:![]() 。
。![]() 为
为![]() 在第
在第![]() 个属性上的取值。
个属性上的取值。![]() 表示
表示![]() 中在第
中在第![]() 个属性上取值为
个属性上取值为![]() 的样本组成的集合。
的样本组成的集合。![]() ,对于贝叶斯网
,对于贝叶斯网![]() 的评分函数可以写成:
的评分函数可以写成:![]()
![]() 是每个参数
是每个参数![]() 所需编码为数,
所需编码为数,![]() 是贝叶斯网的参数个数
是贝叶斯网的参数个数