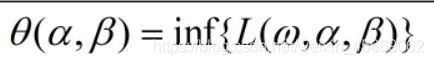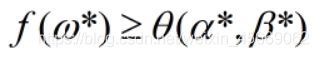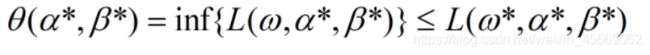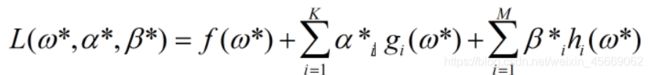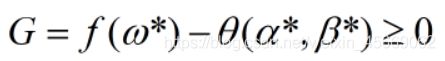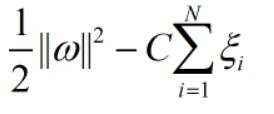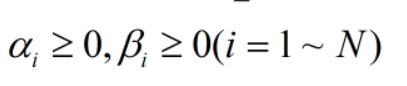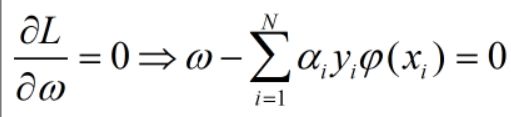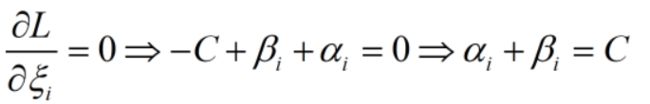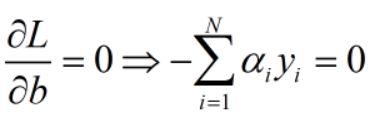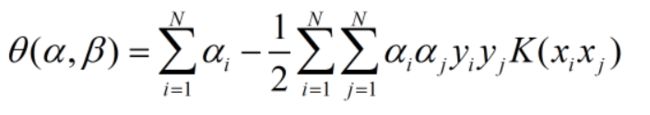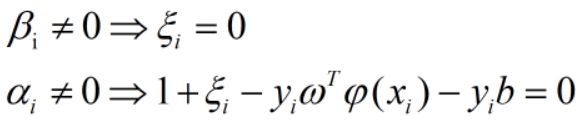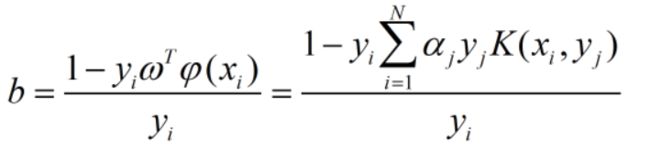机器学习笔记——支持向量机（3）——原问题和对偶问题
引言
在上一节我们介绍了支持向量机svm解决非线性相关的问题。如何利用已知的K和未知的ψ去解决优化问题是关键。在这一节将针对原问题原对偶问题进行学习。
优化理论
原问题（Prime Problem）
最小化：f （ω）
限制条件：① gi（ω）<=0 ( i=1~K )；② hi（ω）=0 （ i=1~M ）
原问题是一个非常普适（general）的定义。
首先，最小化中 ω 是自变量，同时也是向量，待优化参数的自变量。f 是其函数。对于最小化的 f（ω），有最大化的 - f (ω）。
而在限制条件中，分别有K个不等式与M个不等式。对于①式左右两边同时添加负号变为大于等于；对于②式可以变形为 hi(ω) -c =0
综上，原问题具有普适性。
对偶问题(Dural Problem)
定义
L（ω，α，β）
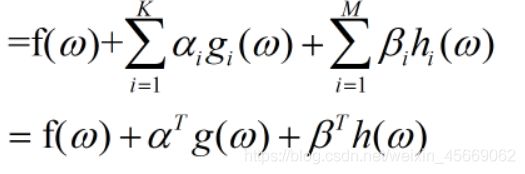
在这个函数中存在三个变量，变量ω是已知的，与原问题中一致。而变量α，β的维度与原问题限制条件保持一致，因此为K维与M维。
对偶问题的定义
最大化：
限制条件： αi >=0 (i=1~K)
最大化中的函数 L 在前面已经定义。inf 称为求最小值，也就是求得后面括号中 L 的最小值。它在固定了α，β的情况下，便历所有的ω，求出L的最小值。 因此我们每确定一个α，β，都会得到一个确定的值，因此这是一个关于α，β的函数θ，与ω无关。 最后，我们针对所有的α，β，求出关于θ的最大值。
原问题与对偶问题的关系
定理：如果 ω* 是原问题的解，而 α* 和 β* 是对偶问题的解，则有：
下面给出证明过程
可得上式等号左右两侧均小于 f（ω）
定义
这里G叫做 原问题与对偶问题的间距（Duality Gap）
对于某一些特定的优化问题，可以证明G=0
强对偶定理
若f（ω）为凸函数，且g（ω）=Aω+b，h（ω）=Cω+d, 则此优化问题的原问题与对偶问题间距为0 即 f（ω*）=θ（α*，β*）
若该等式成立，则由证明过程可以得出 对于∀i=1~K , 要么α*i=0 ，要么g*i（ω*）=0
——————————分割线————————————————————
现在，我们针对svm，提出：
最小化
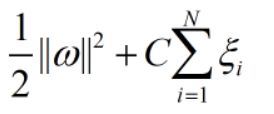
两个限制条件
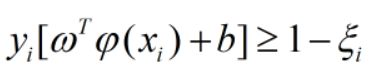
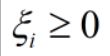
在这里，有最小化对应了原问题的 （ω），同时该最小化时式为凸函数（参考二次函数二次项系数为负的函数图像）
关于凸函数，有：
对于∀ω1，ω2，∀λ∈[0,1]
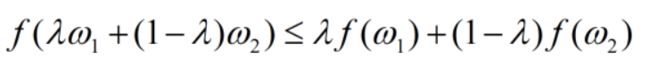
其实这个性质在几何层次上可以轻松被证明，但是我们依然要提出代数层面的解答。原因在于：几何层面的理解仅仅针对于二维平面，而在代数式中的ω1，ω2可以为一个数，同样可以为一个向量，更高维度的自变量。代数式提出了更高维度的解答。
对于这两个限制条件，其与原问题的线性条件存在偏差（大于等于号），因此我们想办法来弥补这个偏差。
修正
最小化：
两个限制条件：
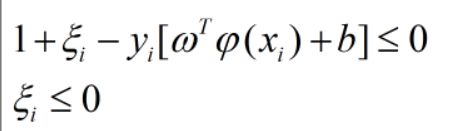
原文题中的g（ω）对应了这里的两个限制条件，于是在这里共有2K个式子（i=1~K），h（ω）没有对应。
接下来把它写成对偶问题
对偶问题
最大化
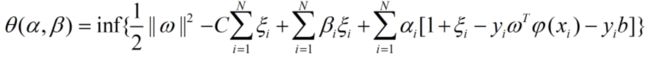inf函数关于所有的ω，ξi，b
式中αi，βi均对应原问题中的α
而原文题中的β在这里是没有的
限制条件
原问题中的α对应式中αi，βi
接下来，我们尝试对这个复杂的最大化式子进行推导，求出在大化θ在满足何条件时最小。
让L分别关于ω，ξi，b进行求导，得到
即上述三式均满足时，θ（α，β）最小
那么如果要求得最小的θ值，那么我们只需要将上述三式的值代入原式
先分部计算，再统一加和
第一项
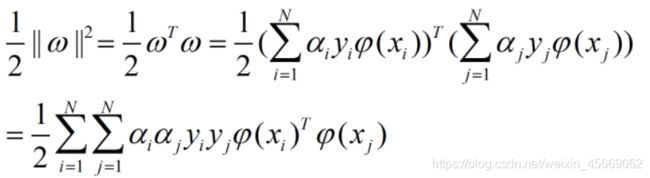
第二项
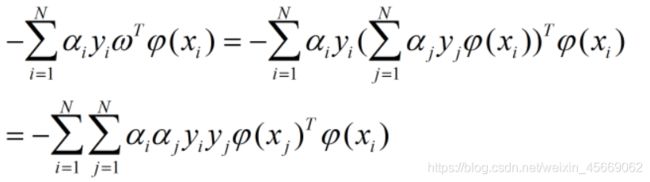
上述第一项与第二项中关于ψ的项可以单独取出，定义为K（xi,yi）
最后将两项相加，得到如下答案
限制条件
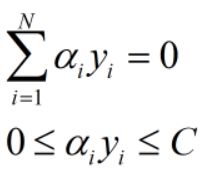
在解决了这个问题之后，我们成功的求出了α，但问题的本质依旧在于求出ω和b。那么如何利用求出的α转化求出ω和b呢？
测试流程
将测试样本x输入
若 ωT ψ（x）+b >= 0 , 则y=+1
若 ωT ψ（x）+b < 0 , 则y=-1
在这里我们可以不知道 ω，只需要知道ωT ψ（x）+b便可解决问题
再将前面得到的ωT代入，得到
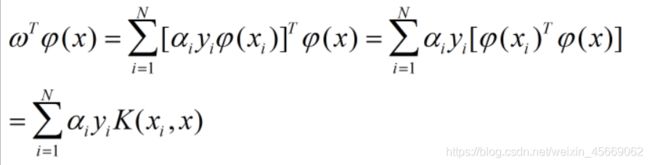
由此可知，我们不见得需要知道ωT ψ（x），只需知道核函数并带入参数，就可以得到ωT ψ（x）的结果
我们再来讨论b的解法
求解b
这里需要使用到KKT条件
KKT条件放在这里的svm中，可以写为：
1.要么 βi = 0,要么ξi = 0
2.要么 αi = 0,要么 1+ ξi - yiωTψ(xi) - yib = 0
取一个0 < αi
此时
最后将等式变形
（创作不易 ，如需转载请联系作者）