论文阅读:BEATNET: CRNN AND PARTICLE FILTERING FOR ONLINE JOINT BEAT DOWNBEAT AND METER TRACKING
BeatNET:用于在线联合节拍弱拍和仪表跟踪的 CRNN 和粒子过滤
BEATNET: CRNN AND PARTICLE FILTERING FOR ONLINE JOINT BEAT DOWNBEAT AND METER TRACKING
开源地址:
https://github.com/mjhydri/BeatNet
论文地址:
https://arxiv.org/abs/2108.03576
摘要
提示:这里可以添加本文要记录的大概内容:
节奏信息的在线估计,例如节拍位置、强拍位置和节拍,对于许多实时音乐应用来说至关重要。 音乐节奏包含跨时间的复杂等级关系,使其分析具有内在的挑战性,有时还具有主观性。 此外,试图实时估计节奏信息的系统必须是因果的,并且必须快速有效地产生估计。
在这项工作中,我们介绍了一个用于联合节拍、强拍和节拍跟踪的在线系统,该系统利用因果卷积和循环层,然后在推理过程中应用一对顺序蒙特卡罗粒子滤波器。
所提出的系统不需要为执行强拍跟踪而准备时间签名,而是能够随着时间的推移估计节拍并调整预测。 此外,我们提出了一种信息门策略,以显着降低推理步骤中粒子滤波的计算成本,使系统比以前基于采样的方法快得多。
在训练期间看不到的 GTZAN 数据集上的实验表明,该系统优于各种在线节拍和强拍跟踪系统,并达到了与基线离线联合方法相当的性能。
提示:以下是本篇文章正文内容,下面案例可供参考
一、pandas是什么?
示例:pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。
一、pandas是什么?
示例:pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。
一、pandas是什么?
示例:pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。
二、使用步骤
1.引入库
算法 1 详细描述了推理过程。 通过从其状态空间内的均匀分布中采样,随机初始化两个推理模块的粒子。 通过进入一个新的帧,节拍状态空间内的粒子通过从转换模型中采样被转移到新的位置,然后计算新的重要性权重并进行归一化。 如果帧的激活满足信息门条件,则对所有粒子调用重新采样过程;
否则,将跳过重新采样步骤,因为它可能是非节拍帧。 之后,如果粒子的中值在节拍区域的容差窗口 Tw 内,并且考虑到估计的节拍,当前帧的时间比上次检测到的节拍足够长,则该帧被分类为节拍帧。 强拍和计量推断模块遵循类似的过程。
推理过程的可视化如图 3 所示。每对图都展示了推理过程的一个步骤,其中顶部和底部的图分别显示了节拍和强拍跟踪过程。 在第一对图中,拍子是随机初始化的。 在第二对中,检测到第一拍,同时随机初始化强拍状态粒子。 在第三对中,拍跟踪粒子已经收敛,但强拍粒子尚未收敛。
这里强拍杂波位于强拍状态空间的最低行,代表六拍拍号。 接下来的几个图对说明了节拍和强拍粒子的收敛,产生了速度和节拍相位(顶部图)以及节拍和小节相位(底部图)的估计。
2.1.特征表示
网络模块的输入是一系列滤波器组幅度响应,每个响应对应一个音频帧。具体来说,将具有 93 ms 长度和 46 ms 跳跃大小的 Hann 窗口的短时傅里叶变换 (STFT) 应用于音频信号以计算对数幅度幅度谱图。然后应用范围从 30 Hz 到 17 kHz 的对数间隔滤波器组,每倍频程 24 个频段,以产生 136 维滤波器组响应。该响应的一阶时间差也被计算和连接,从而为每帧产生一个 272 维的滤波器组响应向量。我们还尝试了替代特征表示,包括来自 [15] 的 329-d 手工制作的特征集,其中包括色度特征、起始强度、低频光谱特征和旋律常数 Q 光谱特征。此功能集的动机是聚合音乐的和声、打击乐、低音和旋律内容。然而,上述 272 维滤波器组响应特征集的性能明显优于这些手工制作的特征,因此被选择用于后续实验。
2.2.网络架构
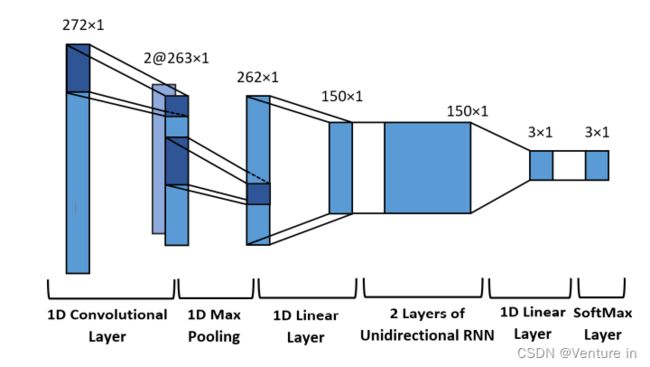
遵循其他类似工作的通用设计,我们采用卷积递归神经网络 (CRNN) 架构(如图 2 所示)来处理输入特征以获得节拍和强拍激活。理想情况下,卷积模型沿着频率轴的关系,而单向递归模型以因果方式跨越时间的长期关系。输入特征被输入到具有 2 个内核大小为 10 的滤波器的 1D 卷积层中,然后是 ReLU 激活。两个滤波器响应在频率上以 2 的内核大小最大池化,然后连接成每个帧的单个特征嵌入。然后,具有 150 个神经元的全连接层降低了嵌入的维数,并将其馈入两个后续的单向长短期记忆 (LSTM) 层,每个层的隐藏大小为 150。嵌入然后馈入最终的完全连接层和softmax操作获得三个激活,分别代表节拍、强拍和非节拍。请注意,由于 softmax 函数,每个类的最终激活总和为 1。
2.3.粒子过滤推理
遵循其他类似工作的通用设计,我们采用卷积递归神经网络 (CRNN) 架构(如图 2 所示)来处理输入特征以获得节拍和强拍激活。理想情况下,卷积模型沿着频率轴的关系,而单向递归模型以因果方式跨越时间的长期关系。输入特征被输入到具有 2 个内核大小为 10 的滤波器的 1D 卷积层中,然后是 ReLU 激活。两个滤波器响应在频率上以 2 的内核大小最大池化,然后连接成每个帧的单个特征嵌入。然后,具有 150 个神经元的全连接层降低了嵌入的维数,并将其馈入两个后续的单向长短期记忆 (LSTM) 层,每个层的隐藏大小为 150。嵌入然后馈入最终的完全连接层和softmax操作获得三个激活,分别代表节拍、强拍和非节拍。请注意,由于 softmax 函数,每个类的最终激活总和为 1。
在我们的案例中,直到第 K 帧为止,我们感兴趣的是基于节拍观察 y1:K 的潜在节拍或强拍位置 x1:K 的以下后验 p(x1:K|y1:K)。 可以根据下面的关键方程推断。 更详细的信息请参考我们之前的工作
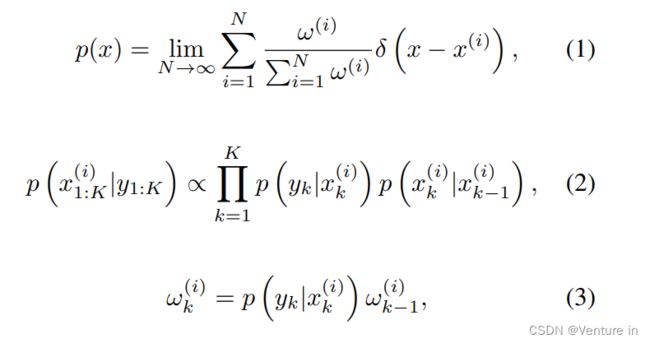
其中ω(i)是粒子i的重要性权重,δ(·)是狄拉克函数。 方程 (1) 描述了使用大量粒子 (N → ∞) 及其重要性权重对 p(x) 的估计。 方程 (2) 是一个动态模型,它使用转换(运动)和观察(校正)概率更新每个帧 k 的后验。 方程(3) 描述了使用当前观察和上一步的重要性权重来更新重要性权重的递归过程。
2.3.1 状态空间、转移和观察模型
我们使用两个顺序蒙特卡罗粒子滤波器的级联,一个用于节拍跟踪,另一个用于强拍和节拍跟踪。 节拍估计器的状态空间和转换模型类似于[32]。 节拍状态空间是一种 2D 小节指针模型,其在帧的相位(水平)和速度(垂直)的转换在方程式中描述。 (4)和(5),分别。 拍间隔内帧 k 的相位和帧 k 处的节拍分别用 φb,k 和 φ˙ b,k 表示。 一个常数 λb 会影响跨节奏轴的潜在跳跃的强度。
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了pandas的使用,而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。