数据挖掘复习
第一章-统计学习
基本分类
- 监督学习
- 无监督学习
- 强化学习
- 半监督,主动学习(接近监督)
三要素
方法=模型+策略+方法
监督学习
分类问题
输入可以离散或连续,输出是有限个离散值
准确率:分类器正确分类与样本总数之比
精确率:TP/TP+FP
召回率:TP/TP+FN
标注问题
输入观测序列,输出标记序列或状态序列
回归问题
预测输入变量和输出变量之间的关系
最常用的损失函数是平方损失函数,用最小二乘法求解
第二章-感知机
感知机(perceptron)是二分类的线性分类模型,输入特征向量,输出实例类别,取+1和-1二值,划分正负两类的分离超平面,属于判别模型。利用梯度下降法对损失函数进行极小化,求得感知机模型。分为原始形式和对偶形式。
f(x)=sign(w·x+b)
w为权值,b为偏置,w·x为内积
对应于特征空间Rn中的一个超平面S,w是超平面的法向量,b是超平面的截距,超平面被划分为两个部分,两部分的点为正负两类。
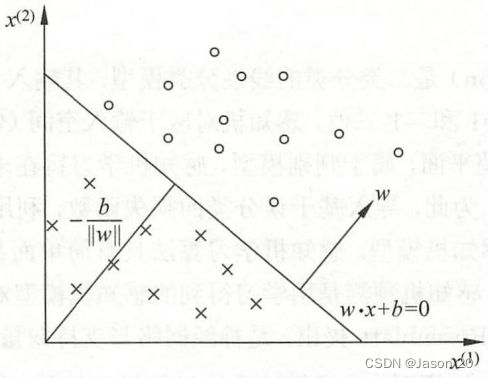
感知机算法对偶形式(例题)

第三章-k近邻法
k近邻法(k-nearest neighbor) 是一种基本分类与回归方法。本次只讨论分类问题。
输入实例的特征向量,对应于特征空间的点,输出为实例的类别,可多类,通过多数表决等方式进行预测。
三要素:k值选择(一般选较小),距离度量,分类决策规则(多数表决)
k近邻法的实现:kd树
第四章-朴素贝叶斯法
朴素贝叶斯(naive Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法。
基于特征条件独立假设学习输入输出的联合概率分布,用此模型对输入x利用贝叶斯定理求出后验概率最大的输出y。
第五章-决策树
决策树(decision tree)是一种基本的分类与回归方法,本次只讨论分类问题
利用if-then规则,或特征空间与类空间上的条件概率分布。
优点:模型可读性,分类速度快
决策树学习:特征选择,决策生成,决策树修剪
第六章-逻辑斯谛回归与最大熵模型
逻辑斯谛回归(logistic regression)是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则,都属于对数线性模型。
逻辑斯谛回归由条件概率P(Y|X)表示,随机变量X取实数,Y取1或0,通过监督学习估计模型参数。
最大熵模型(maximum entropy model)由最大熵原理推导实现。最大熵原理认为学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型时最好的模型,也用约束条件来确定概率模型的集合。
第七章-支持向量机
支持向量机(support vector machines,SVM)是一种二分类模型,基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它区别于感知机。
支持向量机的学习策略就是间隔最大化
支持向量机的学习算法时求解凸二次规划的最优化算法
训练数据线性可分时,通过硬间隔最大化,即线性可分支持向量机,又称硬间隔支持向量机。
通过软间隔最大化,即线性支持向量机,又称软间隔支持向量机。
训练数据线性不可分时,使用核技巧及软间隔最大化,即飞线性支持向量机。
第八章-提升方法
提升(boosting)方法在分类问题中,通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。
AdaBoost算法从训练数据中学习一系列弱分类器或基本分类器,并将这些弱分类器线性组合成为一个强分类器。
提升树算法:以决策树为基函数的提升方法称为提升树,对分类问题决策树是二叉分类树。
第九章-EM算法及其推广
EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计。
EM算法每次迭代由两步组成,E求期望,M求极大,所以也称为期望极大算法。
EM算法的一个重要应用是使用高斯混合模型的参数估计。
- 明确隐变量,写出完全数据的对数似然函数
- EM算法E步,确定Q函数
- EM算法M步,求Q函数极大值,新一轮模型迭代参数
- 重复计算,直到对数似然函数值不再有明显变化
第十章-隐马尔可夫模型
隐马尔可夫模型(hidden Markov model,HMM)是可用于标注问题的统计学习模型,描述由隐藏的马尔可夫链随机生成观测序列的过程,属于生成模型。
隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测从而产生观测随机序列的过程。
前向算法举例
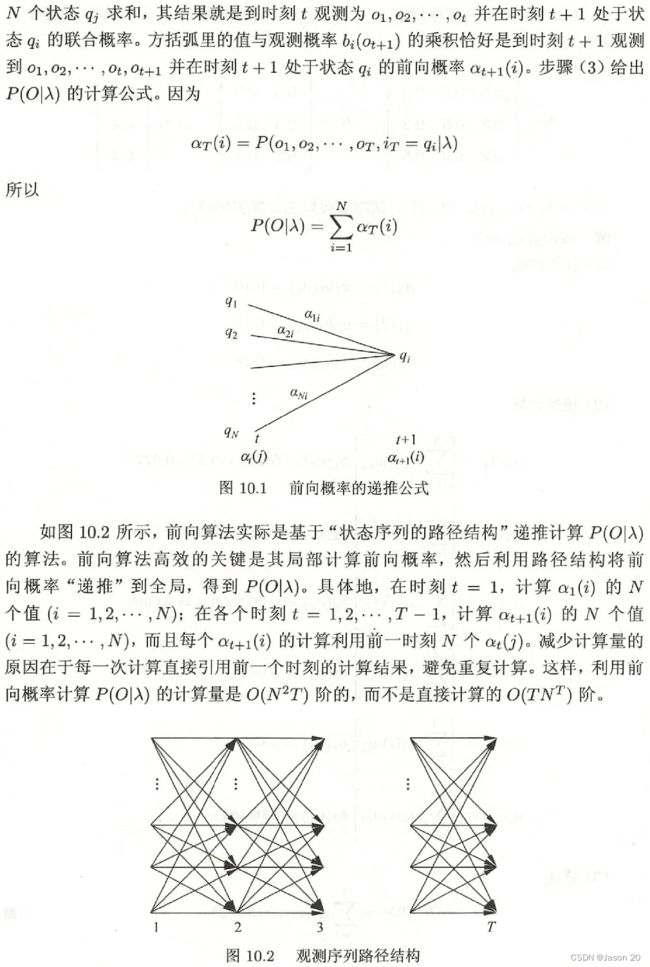
例题:
λ:隐马尔可夫模型,有(A,B,π)
A:状态转移矩阵,表示时刻t处于状态qi的条件下在时刻t+1转移到qj的概率
B:观测概率矩阵,在时刻t处于状态qi下生成观测vk的概率,bj(oi)表示B的第j行第i个
π:初始状态概率向量,t=1处于状态qi的概率
Q:状态集合,长度为N
V:观测集合,长度为M
O:观测序列

第十一章-条件随机场
第十二章-监督学习方法总结
十种主要统计学系方法:
- 感知机
- k近邻法
- 朴素贝叶斯法
- 决策树
- 逻辑斯谛回归与最大熵模型
- 支持向量机
- 提升方法
- EM算法
- 隐马尔可夫模型
- 条件随机场
第十三章-无监督学习概论
无监督学习是从无标注数据中学习模型的机器学习问题。主要包括
- 聚类
- 降维
- 概率模型估计
- 话题分析
- 图分析
第十四章-聚类方法
聚类是针对给定样本,依据他们特征的相似度或距离,将其归并到若干个“类”或“簇”。一个类是给定样本集合的一个子集。样本间相似度或距离起重要作用。
层次聚类:聚合(自下而上),每个样本一个类,不断与最近合并;分裂(自上而下)一个类,不断与最远分开。
k均值聚类(k-means clustering):基于中心,通过迭代将样本分到k个类,是得每个样本与其所属类的中心或均值最近,得到k个划分。
k均值聚类是基于样本集合划分的聚类算法。分k类,每个样本到其所属类的中心距离最小,每个样本只能属于一个类,则k均值聚类是硬聚类。
例题:
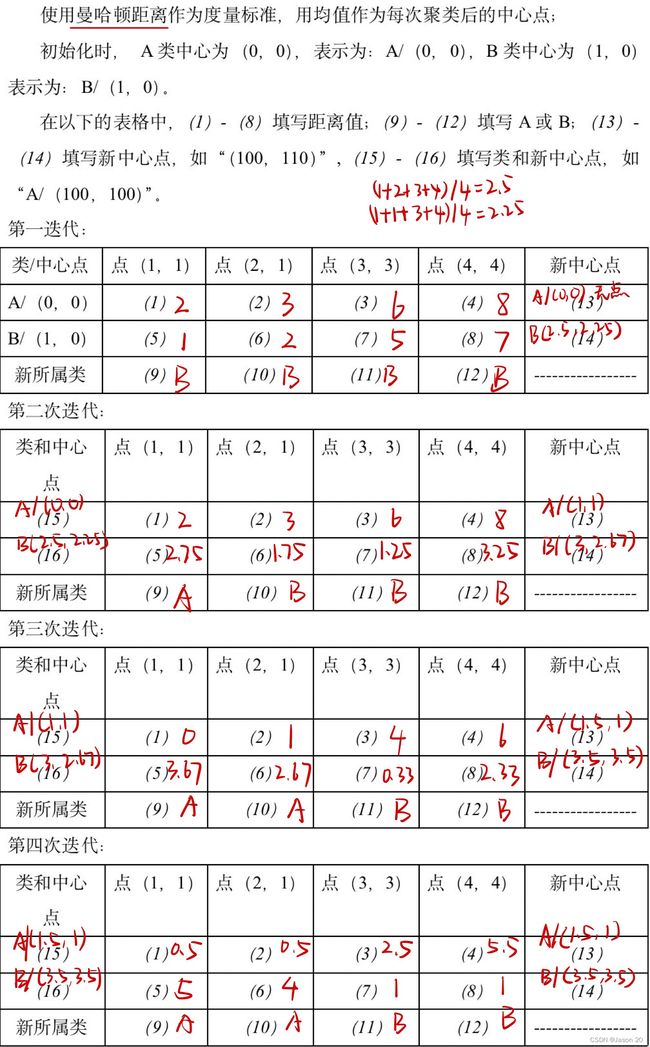
两次聚类结果相同时表明聚类中心不会再更改,即迭代完成
第十五章-奇异值分解
奇异值分解(singular value decomposition,SVD)是一种矩阵因子分解方法。主成分分析会用到奇异值分解。
第十六章-主成分分析
主成分分析(principal component analysis,PCA)是一种常用的无监督学习方法,利用正交变换吧线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据,线性无关变量称为主成分。

计算步骤:

例题:

第十七章-潜在语义分析
潜在语义分析(latent semantic analysis,LSA)无监督学习方法,主要用于文本的话题分析,通过矩阵分解发现文本与单词之间的基于话题的语义关系。
第十八章-概率潜在语义分析
概率潜在语义分析(probabilistic latent semantic analysis,PLSA)也称概率潜在语义索引,是一种利用概率生成模型对文本集合进行话题分析的无监督学习方法。
第十九章-马尔可夫链蒙特卡洛法
蒙特卡罗法(Monte Carlo method)也称为统计模拟方法,是通过从概率模型的随机抽样进行近似数值计算的方法
马尔可夫链(Markov chain)为概率模型的蒙特卡罗法。
马尔可夫链蒙特卡罗法构建一个马尔可夫链,使其平稳分布就是要进行抽烟的分布,先给予马尔可夫链进行随机游走,产生样本序列,之后用平稳分布的样本进行近似数值计算。
第二十章-潜在狄利克雷分配
潜在狄利克雷分配(latent Dirichlet allocation,LDA)基于贝叶斯学习的话题模型,是潜在语义分析,概率潜在语义分析的扩展。
第二十一章-PageRank算法
PageRank算法是图的链接分析的代表性算法,属于图数据上的无监督学习方法。
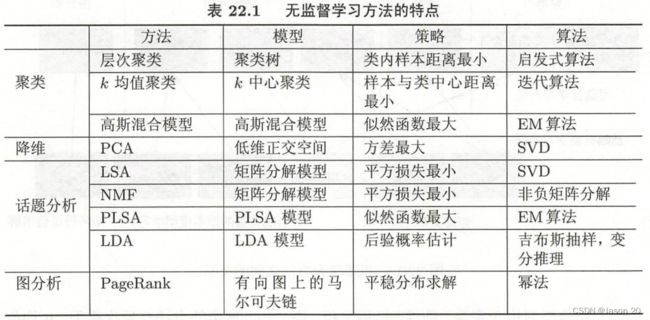
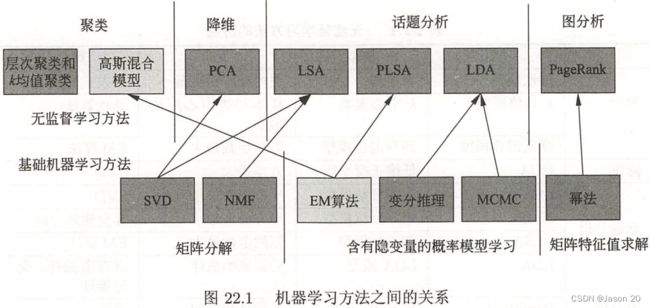
第二十二章-无监督学习方法总结
八种常用统计机器学习方法
- 聚类(层次聚类与k均值聚类)
- 奇异值分解(SVD)
- 主成分分析(PCA)
- 潜在语义分析(LSA)
- 概率潜在语义分析(PLSA)
- 马尔可夫链蒙特卡罗法(MCMC)
- 潜在狄利克雷分配(LDA)
- PageRank算法
梯度下降法
注意要点
- 训练时表现好,测试表现不好,过拟合,要增加数据,正则化(原来误差函数增加处罚项)
- 逻辑回归是分类模型,常见激活函数sigmod,阈值点0.5
- Sklearn常用模型的后缀名,pkl
- sklearn.decomposition.PCA(n_components=None)参数大于一是主成分个数,小于一是保留方差,总体信息的百分比
- 假设空间小(项数少,模型简单,近直线),欠拟合,数据少,过拟合
- 增加样本,新的特征,训练准确率会增加或不变,但测试不一定增加
- 大型数据集训练随机森林决策树,为花费时间更少,要降低树的深度 p67
- 支持向量机和逻辑回归都是分类,区别在于损失函数,线型回归损失函数是均方差,逻辑回归用交叉熵(本质最大似然函数),神经网络分类也用p111 p91
- EM算法,期望最大化,kmeasn,高斯混合模型,隐变量,决定,数据从哪个高斯模型里出(权值),隐变量在的地方 p177
- 常用机器学习优化算法,梯度下降sgd,复杂模型也有很多选择。
- 梯度是既有大小又有方向的向量,指某函数在该点处最大的方向导数,梯度方向就是函数在该点最陡的方向
- 梯度下降sgd,沿着负梯度方向(下降最快)搜索,步长太大可能错过最低点,步长太小计算量会增大,迭代速度太慢,当损失函数不变小,变小情况不好,则取值不够合理。