Python学习（机器学习_线性回归）

本人机械类专业，最近接触python学习，觉得挺有意思。后来在网上看到推荐的机器学习（斯坦福公开课），刚学完线性回归，然后就尝试在python（2.7）上面实现一遍，巩固所学知识的同时也加深对于机器学习的算法的理解。代码基本照搬octave中的作业题答案，在此也很感谢黄海广博士的学习资料，内容真的很详细。
http://mooc.guokr.com/course/16/Machine-Learning/

#Machine_Learning(ex1_Linear Regression)

#part1 basic function
def warmUpExercise():
    A = []
    import numpy as np
    A = np.eye(5)
    print(A)

print "Running warmUpExercise...\n"
print "5*5 Identity Matrix:\n"
warmUpExercise()

#part2 Plotting
print "Wait two seconds"
print "Plotting Data...\n"
import time
time.sleep(2)
#提取数据，数据为两列，单变量
f = open('F:\machinelearning\ex1\ex1data1.txt')
data=[]
for line in f:
    data.append(map(float,line.split(",")))
m=len(data)
X=[]
y=[]
for i in range(0,m):
    X.append(data[i][0])
    y.append(data[i][1])
#绘制散点图
import numpy as np
X=np.array(X)
y=np.array(y)
import matplotlib.pyplot as plt
plt.xlabel("Population of the city(10000s)")
plt.ylabel("Profit($10000)")
Training,=plt.plot(X,y,'o',label='Training data')
#plt.legend(handles=[Training], loc='lower right')
plt.show()

#Part 3: Gradient descent
#求代价函数
def computeCost(X,y,theta):
    J=0
    import numpy as np
    m=len(y)
    #注意X*theta,形式为np.dot(n*m,m*k)
    A=np.dot(X,theta)
    #对应数相乘（*）
    A=(A-y)*(A-y)
    J=sum(A)/(2*m)
    return J

 #通过梯度下降法迭代求解theta   
def gradientDescent(X,y,theta,alpha,num_iters):
    m=len(y)
    import numpy as np
    #初始化J
    J_history=np.zeros(num_iters)
    for iter in range(0,num_iters):
        H=np.dot(X,theta)
        T=np.zeros(2)
        for i in range(0,m):
            T=T+np.dot((H[i]-y[i]),X[i])
    theta=theta-(alpha*T)/m
    J_history[iter]=computeCost(X,y,theta)
    print theta
    return theta,J_history


print "Running Gradient Descent...\n"
one=np.ones(m)
#记得加上转置，这样Size才是m*2
X=(np.vstack((one,X))).T
theta=np.zeros(2)
iterations=1000
alpha=0.01
print "The initial cost is:",computeCost(X,y,theta)
print "Theta found by gradient descent:"
[theta,J_history]=gradientDescent(X, y, theta, alpha, iterations)
print "Final cost is:",J_history[iterations-1]
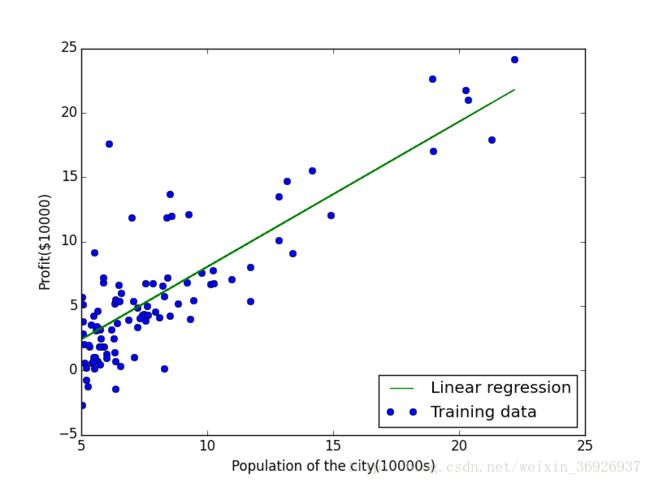
#绘制预测的趋势图像
Y=np.dot(X,theta)
line,=plt.plot(X[:,1],Y,label='Linear regression')
plt.legend(handles=[line,Training], loc='lower right')
plt.show()

#part4 plot surface和contour图
theta0=np.arange(-10,10,20.0/100)
theta1=np.arange(-1,4,5.0/100)
J_history=np.zeros([len(theta0),len(theta1)])
for i in range(0,len(theta0)):
    for j in range(0,len(theta1)):
        t=([theta0[i],theta1[j]])
        J_history[i,j]=computeCost(X,y,t)
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()  
ax = Axes3D(fig) 
ax.plot_surface(theta0,theta1,J_history,rstride=3,cstride=2,cmap=plt.cm.coolwarm,alpha=0.3)
ax.set_xlabel('theta0')  
ax.set_ylabel('theta1')
ax.set_zlabel('J')   
plt.show()
ax.contourf(theta0,theta1,J_history,zdir='z',offset=600,cmap=plt.cm.coolwarm)
x1=[]
x1.append(theta[0])
y1=[]
y1.append(theta[1])
z1=[600]
plt.plot(x1,y1,z1,'*')
plt.show()

结果为：
Running warmUpExercise…

5*5 Identity Matrix:

[[ 1. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 1.]]
wait two seconds
Plotting Data…

Running Gradient Descent…

The initial cost is: 32.0727338775
Theta found by gradient descent:
[-3.24140214 1.1272942 ]
Final cost is: 4.51595550308

折腾了好久，终于勉强码完，很多包我其实现学现用，功能太强大，也不是一天能够写完，只能先告一段落，以后慢慢修改完善。比如：对于Axes3D中的一个小模块就有很多要学习的。

>>> help(Axes3D(fig).plot_surface)
Help on method plot_surface in module mpl_toolkits.mplot3d.axes3d:

plot_surface(self, X, Y, Z, *args, **kwargs) method of mpl_toolkits.mplot3d.axes3d.Axes3D instance
    Create a surface plot.

    By default it will be colored in shades of a solid color,
    but it also supports color mapping by supplying the *cmap*
    argument.

    The `rstride` and `cstride` kwargs set the stride used to
    sample the input data to generate the graph.  If 1k by 1k
    arrays are passed in the default values for the strides will
    result in a 100x100 grid being plotted.

    ============= ================================================
    Argument      Description
    ============= ================================================
    *X*, *Y*, *Z* Data values as 2D arrays
    *rstride*     Array row stride (step size), defaults to 10
    *cstride*     Array column stride (step size), defaults to 10
    *color*       Color of the surface patches
    *cmap*        A colormap for the surface patches.
    *facecolors*  Face colors for the individual patches
    *norm*        An instance of Normalize to map values to colors
    *vmin*        Minimum value to map
    *vmax*        Maximum value to map
    *shade*       Whether to shade the facecolors
    ============= ================================================

    Other arguments are passed on to
    :class:`~mpl_toolkits.mplot3d.art3d.Poly3DCollection`