2012_ImageNet Classification with Deep Convolutional Neural Networks
文章目录
- 1. Title
- 2. Summary
- 3. Problem Statement
- 4. Method(s)
-
- 4.1 Introduction
-
- 4.1.1 ImageNet 数据集
- 4.1.2 卷积神经网络(Convolutional Neural Network)
- 4.2 模型结构
-
- 4.2.1 ReLU 激活函数
- 4.2.2 多 GPU 并行处理
- 4.2.3 局部响应归一化(Local Response Normalization)
- 4.2.4 重叠池化 Overlapping Pooling
- 4.2.5 整体结构
- 4.3 减轻过拟合现象的几个策略
-
- 4.3.1 数据增强
-
- 4.3.1.1 增强方案 1
- 4.3.1.2 增强方案 2
- 4.3.2 Dropout
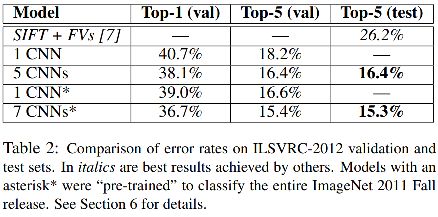
- 5. Results
1. Title
文章链接:ImageNet Classification with Deep Convolutional Neural Networks
Pytorch 参考代码:AlexNet
2. Summary
AlexNet 作为深度学习的复兴之作,使得 CNN 开始逐渐在计算机视觉领域开始占据主导地位。
AlexNet 模型结构的搭建方面放到现在没有太多可说的,但是对于分组卷积、Local Response Normalization、Dropout 等概念以及代码的理解也是值得一看的。
3. Problem Statement
主要目标就是进一步地提升分类模型的精度,并再次将深度学习引入了大众视野。
4. Method(s)
本文设计并训练了一个 5 层卷积+3 个全连接层的超大卷积神经网络,并使用了当时很多较为先进的模块和技术,使得大模型的训练成为可能,同时一定程度上缓解了大模型的过拟合问题。
4.1 Introduction
对于较为简单的视觉任务来说,之前的较小规模的数据集也足以完成任务。但是现实生活中的目标更为丰富多样,需要更大的数据集来完成相应的识别任务。而与此同时,ImageNet 数据集诞生了。
4.1.1 ImageNet 数据集
ImageNet是一个包含了 1500 万张带有标注的高质量数据集,其提供大约 2.2 万个类别的标注。这个数据集目前称之为ImageNet-22k。而本文是在基于该数据集的一个子集上完成的。该子集称为ImageNet-1k,一共提供了 1000 个类别的标注,每个类别提供了大约 1000 张图片。总体而言,ImageNet-1k大约有 120 万的训练图片,5 万的验证图片和 15 万的测试图片。
在该数据集上,一般报告两个分类指标:Top-1 和 Top-5 准确率。
该数据集中提供的图片的分辨率是多种多样的,本文对该数据集进行了预处理。
- 将图片下采样至 256x256 的尺寸。
- 对原图进行 rescale,使得最短边长度为 256。
- 将 rescale 后的图中央的 256x256 的 patch 裁剪出来。
- 均值化
对于每个像素减去一个均值,该均值由训练集上的所有图片计算得到。
4.1.2 卷积神经网络(Convolutional Neural Network)
对于规模更大的数据集,我们需要一个具有更强大学习能力的模型。
CNN 对于图像的处理,具有一系列的优势:
- 模型容量可以通过模型的深度和宽度来控制。
- 具有强而合理的先验假设。
- 相较于同等层数的全连接网络来说,连接更为稀疏,参数量更少,更容易优化。
4.2 模型结构
文中重点介绍了几个设计或者是模块,这些设计和模块对于 AlexNet 的诞生有着重要的影响。
4.2.1 ReLU 激活函数
之前对于神经元的输出的建模大多使用的是 f ( x ) = t a n h ( x ) f(x)=tanh(x) f(x)=tanh(x)或者是 f ( x ) = ( 1 + e − x ) − 1 f(x)=(1+e^{-x})^{-1} f(x)=(1+e−x)−1这种饱和性非线性函数(所谓饱和性就是说函数的输出会被限定在一定的范围内),而本文则改用了一种更为简单的非线性激活函数 Rectified Linear Units (ReLUs) f ( x ) = m a x ( x , 0 ) f(x)=max(x,0) f(x)=max(x,0)。这种激活函数最大的优点在于其前向以及反向传播的计算都很简单,而且不太会出现梯度消失或者爆炸的情况,比较容易训练和收敛。
并且本文也在一个 4 层的卷积神经网络做了实验,对比了使用 ReLU 和 Tanh 两种激活函数的收敛速度:

可以发现在达到同样的正确率的情况下,使用 ReLU 的模型收敛得更快,从而极大地减少了训练所需要的时间。
4.2.2 多 GPU 并行处理
受到当时计算资源的限制,本文将 AlexNet 分到了两块 GPU 上进行计算,对于有些层来说,其计算仅在某块单独的 GPU 内部进行,而两块 GPU 间不会进行交互。具体而言,对于某个输入特征图,其 shape 为 B ∗ C ∗ H ∗ W B*C*H*W B∗C∗H∗W,其会被平均划分为两个组,每个组的特征图的 shape 变为 B ∗ C 2 ∗ H ∗ W B*\frac{C}{2}*H*W B∗2C∗H∗W,然后相关的卷积或者其他操作仅会在每个组内的特征图内部进行计算,两个组之间不会产生联系。这里实际上诞生了分组卷积的思想。
分组卷积的一个较大的好处是可以较为显著地降低参数量和计算量。
- 普通卷积参数量和计算量
对于一个输入 shape 为 B ∗ C i ∗ H ∗ W B*C_i*H*W B∗Ci∗H∗W的特征图来说,假设我们使用的卷积核的大小为 k ∗ k ∗ C i k*k*C_i k∗k∗Ci,一共使用了 C o C_o Co个不同的卷积核,那么输出的特征图的大小为 B ∗ C o ∗ H ∗ W B*C_o*H*W B∗Co∗H∗W。(这里假设通过 padding 后,特征图的长宽不变)。那么该计算过程的参数量为: k ∗ k ∗ C i ∗ C o k*k*C_i*C_o k∗k∗Ci∗Co,计算量为: B ∗ C o ∗ H ∗ W ∗ k ∗ k ∗ C i B*C_o*H*W*k*k*C_i B∗Co∗H∗W∗k∗k∗Ci(可以这么计算:输出的特征图的大小为 B ∗ C o ∗ H ∗ W B*C_o*H*W B∗Co∗H∗W,每个像素点的值都是一个 k ∗ k ∗ C i k*k*C_i k∗k∗Ci大小的核点乘求和得到的,因此,总的计算量大致为 B ∗ C o ∗ H ∗ W ∗ k ∗ k ∗ C i B*C_o*H*W*k*k*C_i B∗Co∗H∗W∗k∗k∗Ci)。 - 分组卷积计算量
对于一个输入 shape 为 B ∗ C i ∗ H ∗ W B*C_i*H*W B∗Ci∗H∗W的特征图来说,假设我们使用了 g g g组的分组卷积,每组卷积核的大小为 k ∗ k ∗ C i g k*k*\frac{C_i}{g} k∗k∗gCi,每组都使用了 C o g \frac{C_o}{g} gCo个不同的卷积核,那么每组输出的特征图的大小为 B ∗ C o g ∗ H ∗ W B*\frac{C_o}{g}*H*W B∗gCo∗H∗W。(这里假设通过 padding 后,特征图的长宽不变)。那么对于每个组来说,该计算过程的参数量为: k ∗ k ∗ C i g ∗ C o g k*k*\frac{C_i}{g}*\frac{C_o}{g} k∗k∗gCi∗gCo,计算量为: B ∗ C o g ∗ H ∗ W ∗ k ∗ k ∗ C i g B*\frac{C_o}{g}*H*W*k*k*\frac{C_i}{g} B∗gCo∗H∗W∗k∗k∗gCi。总的参数和计算量则是所有组的参数和计算量的和,分别是: k ∗ k ∗ C i C o g k*k*C_i\frac{C_o}{g} k∗k∗CigCo和 B ∗ C o ∗ H ∗ W ∗ k ∗ k ∗ C i g B*C_o*H*W*k*k*\frac{C_i}{g} B∗Co∗H∗W∗k∗k∗gCi。也就是说,整体参数量和计算量都会变为原来的 1 g \frac{1}{g} g1。
不过本文并没有在所有的卷积操作上使用分组卷积,而把这个选择作为了一个超参进行交叉验证调试。
4.2.3 局部响应归一化(Local Response Normalization)
局部响应归一化的动机来源于神经生物学上的一种“侧抑制”的概念:即被激活的神经元会抑制相邻神经元的一种现象,这里需要明确的是,局部响应归一化是对响应进行后处理的一种操作,也就是说,需要先通过全连接或者卷积神经网络前传得到响应后,再针对响应值进行后处理归一化。在具体使用过程中,我们需要明确的是“神经元”的概念。
对于全连接神经网络来说,神经元的概念比较好理解,“侧抑制”的概念就可以理解为,即对于全连接的各个输出响应来说,其需要对相邻的响应进行抑制。
举例说明,对于一个 N N N个神经元的全连接输出来说,其得到 N N N个输出值,或者称为响应(Response),那么,局部响应归一化定义为:
b i = a i / ( k + α ∑ j = max ( 0 , i − n / 2 ) min ( N − 1 , i + n / 2 ) ( a j ) 2 ) β b^{i}=a^{i} /\left(k+\alpha \sum_{j=\max (0, i-n / 2)}^{\min (N-1, i+n / 2)}\left(a^{j}\right)^{2}\right)^{\beta} bi=ai/⎝⎛k+αj=max(0,i−n/2)∑min(N−1,i+n/2)(aj)2⎠⎞β其中, i ∈ N i \in N i∈N表示神经元的各个位置, n n n表示相邻神经元的范围, k k k, α \alpha α, β \beta β都是用于数值调节的超参数。
类比全连接网络,我们可以分析一下卷积神经网络。对于某个卷积神经网络的输出来说,假设其大小为 C ∗ H ∗ W C*H*W C∗H∗W,对于每个位置 ( x , y ) , x ∈ H , y ∈ W (x,y),x\in H,y\in W (x,y),x∈H,y∈W来说,其由 C C C个响应值,如果单看某个 ( x , y ) (x,y) (x,y),其情况和一个神经元个数为 C C C的全连接神经网络类似,因此,我们不难推导出AlexNet文中的公式:
b x , y i = a x , y i / ( k + α ∑ j = max ( 0 , i − n / 2 ) min ( N − 1 , i + n / 2 ) ( a x , y j ) 2 ) β b_{x, y}^{i}=a_{x, y}^{i} /\left(k+\alpha \sum_{j=\max (0, i-n / 2)}^{\min (N-1, i+n / 2)}\left(a_{x, y}^{j}\right)^{2}\right)^{\beta} bx,yi=ax,yi/⎝⎛k+αj=max(0,i−n/2)∑min(N−1,i+n/2)(ax,yj)2⎠⎞β
该操作的本质上就是对每个位置的激活值进行了归一化,使得对于 n n n个相邻的神经元来说,激活值较大的神经元的激活值会较大,而激活值较小的神经元的激活值会变小。
LRN 是对 Channel 进行归一化的一种方式,目前 pytorch 也有官方的实现:torch.nn.LocalResponseNorm(),可以参考其具体代码进行理解,这里也对其做简单解释。
def local_response_norm(input, size, alpha=1e-4, beta=0.75, k=1.):
# type: (Tensor, int, float, float, float) -> Tensor
r"""Applies local response normalization over an input signal composed of
several input planes, where channels occupy the second dimension.
Applies normalization across channels.
See :class:`~torch.nn.LocalResponseNorm` for details.
"""
if not torch.jit.is_scripting():
if type(input) is not Tensor and has_torch_function((input,)):
return handle_torch_function(
local_response_norm, (input,), input, size, alpha=alpha, beta=beta, k=k)
dim = input.dim()
if dim < 3:
raise ValueError('Expected 3D or higher dimensionality \
input (got {} dimensions)'.format(dim))
# div即为原公式中的分母部分。
# 核心即为一个大小为size的窗口的内的求和操作,这里采用的是AveragePooling的方式进行的实现。(由于AveragePooling是个平均操作,和原公式的求和操作存在着一个常数size的差异)
# 由于AveragePooling作用于Channel后的维度,即第2个维度及以后。
# 而LRN作用于Channel维度,因此,需要将Channel后移一个维度,这里就是用的是unqueeze操作进行占位操作,
# 使得AveragePooling可以作用于Channel维度,从而实现核心操作:一个大小为size的窗口的内的求和操作。
div = input.mul(input).unsqueeze(1)
if dim == 3:
div = pad(div, (0, 0, size // 2, (size - 1) // 2)) # padding操作处理边界情况
div = avg_pool2d(div, (size, 1), stride=1).squeeze(1) # 除了Channel那个维度外的kernel size设置为1,使得avg操作对其他维度不产生影响
else:
sizes = input.size()
div = div.view(sizes[0], 1, sizes[1], sizes[2], -1)
div = pad(div, (0, 0, 0, 0, size // 2, (size - 1) // 2))
div = avg_pool3d(div, (size, 1, 1), stride=1).squeeze(1)
div = div.view(sizes)
div = div.mul(alpha).add(k).pow(beta)
return input / div
以上是其核心代码,关键部分加上了注释,可以对照注释进行理解:
div 即为原公式中的分母部分。
核心即为一个大小为 size 的窗口的内的求和操作,这里采用的是 AveragePooling 的方式进行的实现。(由于 AveragePooling 是个平均操作,和原公式的求和操作存在着一个常数 size 的差异)
由于 AveragePooling 作用于 Channel 后的维度,即第 2 个维度及以后。
而 LRN 作用于 Channel 维度,因此,需要将 Channel 后移一个维度,这里就是用的是 unqueeze 操作进行占位操作,
使得 AveragePooling 可以作用于 Channel 维度,从而实现核心操作:一个大小为 size 的窗口的内的求和操作。
4.2.4 重叠池化 Overlapping Pooling
AlexNet 还强调了重叠池化的作用。重叠池化实际上就是池化的 kernel size 大于 stride 的情况。这个可能更多的是实验结果吧,没有理论的依据。
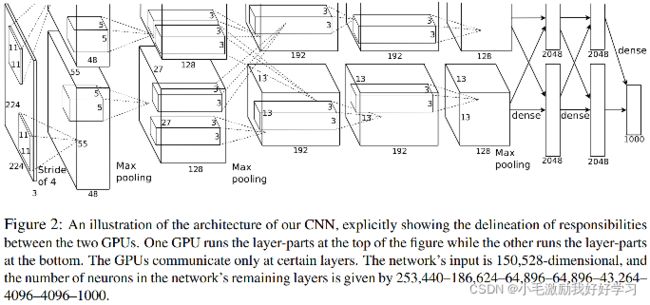
4.2.5 整体结构
上图是 AlexNet 的整体结构图,就模型设计上而言,放到现在来说的话,没有太多可值得说道的内容。整体还是遵循着卷积层提特征降维,全连接层完成分类任务的范式。不过其存在着以下几个不同的设计:
- 在第二、第四和第五个卷积层使用的是分组卷积。
- 在第一个和第二个卷积后使用了 LRN。
- 重叠池化在 LRN 和最后一个卷积层后使用。
- ReLU 激活函数应用于所有的卷积和全连接层。
具体的每个卷积的 kernel 以及 channel 的设置这里就不展开写了,具体可以参考论文及相关代码。
4.3 减轻过拟合现象的几个策略
由于 AlexNet 使用了三个全连接层,参数量很大,存在着较大的过拟合风险,因此,AlexNet 也采用了大量的减轻过拟合的策略。
4.3.1 数据增强
4.3.1.1 增强方案 1
AlexNet 生成了很多相关的图片以扩大数据集的数量。
对于原始处理后的 256x256 的图片,对其进行 224x224 大小的随机裁剪,AlexNet 将在这些裁剪后的 patch 上进行训练。这个策略配合上水平翻转理论上可以扩大数据集 2048 倍( ( 256 − 224 ) ∗ ( 256 − 224 ) ∗ 2 = 32 ∗ 32 ∗ 2 = 2048 (256-224)*(256-224)*2=32*32*2=2048 (256−224)∗(256−224)∗2=32∗32∗2=2048)。尽管这些数据之间具有高度的相关性,但这个策略还是极大地缓解了 AlexNet 的过拟合问题。
测试阶段使用了测试时增强(TestingTimeAugmentation,TTA),即得到 256x256 的图片的四个角以及中心的 5 个 224x224 的 patch 及其水平翻转的 patch,一共 10 个 patch,并对其 10 个预测结果进行平均。
4.3.1.2 增强方案 2
AlexNet 还对训练集图片的 RGB 三通道采用了一种 PCA Jittering。这个策略可以参考这一篇博客,我觉得讲得挺好的。
4.3.2 Dropout
Dropout 也是现在依然经常使用的一种减轻过拟合的策略。其具体做法就是每个神经元在前传过程中以一定的概率 p p p进行“失活”,“失活”的意思是指其不会对前传的结果产生影响,也不会参与反向传播。
Dropout 可以减轻神经元之间的协同适应性,使得神经元不能依赖于其他的神经元,从而习得更具有鲁棒性的特征。
测试阶段时,需要对结果的概率分布进行调整,乘以 1 − p 1-p 1−p,使得其概率分布与训练时基本保持一致。
提供一个相关的 Dropout 的 pytorch 代码:
"""
Borrowed from https://blog.csdn.net/qq_37555071/article/details/107801384
"""
import numpy as np
import torch
import torch.nn as nn
class Dropout(nn.Module):
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x):
if self.training:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
5. Results