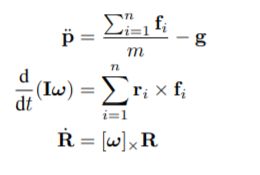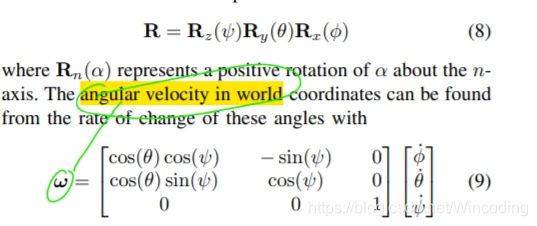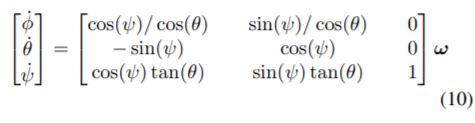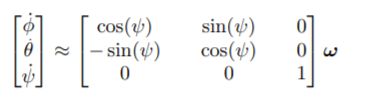- LeetCode - 3274. Check if Two Chessboard Squares Have the Same Color
阿蒙Armon
LeetCodeleetcode算法职场和发展
LeetCode-3274.CheckifTwoChessboardSquaresHavetheSameColor在LeetCode的算法题库中,有许多有趣的题目将实际场景与编程逻辑相结合,LeetCode3274题CheckifTwoChessboardSquaresHavetheSameColor便是其中之一。这道题以国际象棋棋盘为背景,要求我们判断给定的两个方格颜色是否相同。通过解决这道题,
- 美团外卖券购买攻略,如何轻松获取优惠?
高省APP
美团外卖凭借其便捷的服务和丰富的选择,成为了许多消费者日常用餐的首选。而美团外卖券作为一种常见的优惠方式,更是受到了广大用户的青睐。那么,如何购买美团外卖券呢?本文将为您详细解答,并带您了解购买过程中的注意事项。都在挣钱!推荐个月入几千到几万的靠谱副业项目!月入十万必看!都在挣钱!推荐几个月入几千到几万的靠谱副业项目!(公众号:善士思维笔记)公众号流量主就找善士导师(shanshi2024)公众号
- 算法竞赛备考冲刺必刷题(C++) | 洛谷 P1024 一元三次方程求解
热爱编程的通信人
c++算法开发语言
本文分享的必刷题目是从蓝桥云课、洛谷、AcWing等知名刷题平台精心挑选而来,并结合各平台提供的算法标签和难度等级进行了系统分类。题目涵盖了从基础到进阶的多种算法和数据结构,旨在为不同阶段的编程学习者提供一条清晰、平稳的学习提升路径。欢迎大家订阅我的专栏:算法题解:C++与Python实现!附上汇总贴:
- 高省是什么? 高省最高级别是什么
高省APP
现在高省很火,经常有伙伴来问我:高省是什么?高省是不是真的赚钱?高省的各个级别怎么升级?高省的各级别的收益怎么分配?今天我就和大家详细说一下高省是以抖音快手直播电商为主,结合淘宝、京东等传统电商平台为一体的分佣平台,没有高省之前,在抖音快手等平台购物,购物完成后,并不会有返现,也就是说你买100元的商品,你需要支付100元,并且平台也不会给你返1分钱有了高省之后,通过高省再跳转到抖音、快手平台购物
- 处理Electron Builder 创建新进程错误 spawn ENOMEM
这个错误spawnENOMEM表明系统内存不足,无法为ElectronBuilder创建新进程。以下是一些可能的解决方案:释放系统内存关闭不必要的程序和服务增加物理内存(RAM)或交换空间(swap)使用free-h和top命令检查内存使用情况临时增加交换空间#创建一个4G的交换文件sudofallocate-l4G/swapfilesudochmod600/swapfilesudomkswap/
- 解忧信件5648
鱼羊姑娘
第5648封来信爷爷你好:我从小是单亲,跟着爸爸,妈妈在我八九岁的时候就当着我的面离开了,后来回来直接离婚又走了,这对我伤害很大我一直觉得我妈妈不爱我,因为她有了特别好的老公,还生了一个女儿。所以是不需要我的所以从小我自卑,胆怯,讨好型人格,不敢表达自己的感受,不敢开别人玩笑,总是被别人语言上欺负高三我拼了命地努力,却只考上了二本,而且还带给了我影响我身体方方面面的慢性疾病,甲亢会影响我生育,月经
- 复刻劳力士绿水鬼多少钱(复刻绿水鬼价格一览表)
潮品会
劳力士绿水鬼,作为腕表界的经典之作,其独特的设计和卓越的品质赢得了无数表迷的喜爱。然而,由于其高昂的原版价格,许多消费者转而寻求复刻版以满足对这款经典手表的向往【重要提醒】文章最下面有联系方式那么,复刻劳力士绿水鬼到底多少钱呢?将带您一探究竟。一、价格范围概览复刻劳力士绿水鬼的价格因品质、制作工艺及市场波动而异,大致可以划分为几个不同的区间。从几百元到数万元不等,消费者可以根据自己的需求和预算进行
- 交流时, 我们为什么总在人身攻击
陌陌的邮箱
有一次,同学的书遗忘在教室,让我陪他去取,我表示答应,嘴上顺口说了一句:“你可真是一个丢三落四的人”没想到同学听完这句话轻轻地皱了皱眉头,然后一本正经地对我说:“你不应该这样随意定义一个人,很不礼貌”听了他的话,我当时只是有些诧异。但随后的一整天我开始思考,竟然陷入了深深的恐惧之中。我说出“你是一个丢三落四的人。”这句话时,我自己都没有意识到,这实质上是一种极不负责,毫无根据的人身攻击。我仅仅因为
- 七里香细雨绵绵海蓝梦(老周楚轻染谷雨梦过山风)完结小说大全_热门的网络小说七里香细雨绵绵海蓝梦老周楚轻染谷雨梦过山风
晚晚美文
《七里香》主角:老周楚轻染,简介:前几天,老周来城里办事,住进了继子王涛的出租屋里。在见到继子小女友的那一刻,老周顿时惊为天人。这一刻,老周感觉自己呼吸都快要停止了。赶忙装作一副治病救人的模样说:“轻染,你现在躺在床上,咱们开始吧!”“一定要躺在床上吗?”楚轻染有些为难道。“对呀,不躺下去,叔没有办法给你按呀!”“好吧...”楚轻染相信了老周的话,咬了咬牙躺在她和王涛的大床上。这一刻,她感觉羞耻到
- CentOS 清理技巧
老罗技术
centoslinux运维
✅1.查看磁盘使用情况(补充)查看inode使用情况,避免因inode用尽导致写入失败:df-i排序显示当前目录下各文件夹所占空间:du-sh*|sort-hr|head-n20✅2.清理日志文件(增强)对gzip压缩的旧日志也清理:find/var/log-name"*.gz"-mtime+30-execrm-f{}\;定期压缩+删除旧日志建议结合logrotate:示例配置:/etc/logr
- 麦吉丽一般几折拿货?麦吉丽代理拿货价格表?
广州时尚王子
麦吉丽等级分:A类、B类、C类三个等级划分详细了解可以M麦吉丽芹大元老➕qin201262加入麦吉丽代理的费用根据不同的代理级别有所不同vx:qin201262具体如下:C级代理:首批货款7500元,保证金1000元。B级代理:首批货款28000元,保证金3000元。A级代理:首批货款120000元,保证金10000元。需要注意的是,保证金是可以全额退款的麦吉丽护肤品代理,麦吉丽素颜三部曲总代理,
- 虚拟机Ubuntu搭建gitlab服务器,ssh连接
yizhiyu_hh
服务器ubuntugitlab
任务:在一台新的计算机上搭建gitlab环境,用于版本管理并使用ssh连接要求:1、要在Windows系统下运行2、gitlab可以在局域网内被任何pc访问3、搭建完后,使用ssh工具管理4、工具要免费SP1:下载安装虚拟机和ubuntu系统虚拟机选择virtualbox,链接https://www.virtualbox.org/wiki/Downloads现在的virtualbox版本都比较高,
- 《有钱人和你想的不一样》共读 第二篇 财富档案7
橙澄读书写作
金句分享:1人与积极的成功人士交往。穷人与消极的人或不成功的人交往。(真的有这种感觉,跟对圈子很重要,三观不同的人不宜交往太密,远离那些总是消极、负能量的人)2成功的人会把其他成功的人当做激励自己的动力,把其他的成功人士看成学习对象,告诉自己如果他们做得到,我也可以。3模仿,是人最主要的学习方式。4有钱人会感谢在他们之前就已经成功的人,因为他们提供了模范供人追随,让别人比较容易获得成功。5你的目标
- 从空白的头脑,写出丰富的宝藏
迷恋成长
图片发自App有时候中午,午休之后,头脑会发蒙,容易发呆。我不太喜欢这种头脑空白的感觉。我打算还是要写点东西。好像大脑这个东西,会有活跃期,也有懒惰期。在这种情况下,我打开电脑,我想噼里啪啦的写起来。无论写点什么都好,就是不想浪费时间,坐在那里,好像失忆的感觉。写文章,写一本,这是一种不错的活法。我的激情,我的灵感,都在敲打文字的过程中产生。不仅如此,我还在这个过程中看到我的专注。一个人,完全地沉
- gym 安装
ZPC8210
AI强化学习算法python开发语言
安装OpenAIGym的详细指南,涵盖不同版本和扩展组件的安装方法:1.基础安装(核心功能)使用pip安装:bashpipinstallgym使用conda安装:bashcondainstall-cconda-forgegym2.完整安装(包含所有官方环境)bashpipinstallgym[all]注意:这会安装所有依赖,包括MuJoCo等专有环境(需要额外许可证)3.版本选择安装经典版本(0.
- ros2 server 可以设置命令同时获取位置
一个自定义服务SetCommandGetPose.srv:请求字段float32command响应字段geometry_msgs/Posepose服务端收到请求后,把command缓存下来,再把当前位姿填进响应返回。为了便于演示,位置用一个简单计数器模拟;你可以把它替换成TF、里程计或SLAM输出。一、创建功能包bash复制ros2pkgcreate--build-typeament_cmakep
- 苏轻语许流年《失望叠加爱已消失》完结版阅读_(失望叠加爱已消失)全集阅读
热门小说_2
书名:失望叠加爱已消失主角:苏轻语许流年简介:【许流年,你给我听好了,我苏轻语这辈子都不打算生孩子,因为没有任何男人,值得我为他承受十月怀胎的苦!】>>>>>>>请前往文章底部全文完整免费阅读>>>>>>>>>戳我继续阅读<<<<<<<<<<关注微信公众号【书香朗阅】去回个书名或主配角,即可免费阅读【失望叠加爱已消失】小说全文!
- 天空
冰夫
亮蓝的天空,透白的云朵。天空像一本无字之书,引导人们驻足仰望,穿过那些风云雨雪,在浩大的天幕上读懂神秘的生命。用天真的蓝色描绘,用多彩的虹云点缀,叙述天空的故事,排解生活的烦扰,放牧寂寞的灵魂,看太阳在新的一天升起。
- 四种人物形象的描写
夏林曦
关于20-25岁的城市女性的描写:继续上学是昕峄一直以来的梦想。她知道自己已经25岁了,再不拼一下就更没机会了。经过她头悬梁锥刺股般的努力,她终于考进一所理想的大学,即将开始她读博的学习生涯。周围亲友好心提醒昕峄,该找对象了,她听了只是一笑了之。找对象?现在她还没有落实工作,该怎么找,找什么样的合适?想起这些她就头大。不管了,先上学再说。离开学还有几个月的时间,昕峄找了一份临时工作,她得为自己挣点
- 【docker】AnythingLLM的docker-compose及一些启动踩坑
BigBigHang
dockerAIdocker容器ai
摘要:使用docker-compose配置和启动AnythingLLM服务。配置包括指定镜像、设置容器名称、端口映射、数据卷挂载等。通过docker-compose启动AnythingLLM可以进行以下配置:services:anythingllm:image:docker.io/mintplexlabs/anythingllm:latestcontainer_name:anythingllmpo
- Valentino 钱包怎么买便宜?钱包怎么选,钱包推荐
直返APP抖音优惠券
天要给大家分享一款超级美丽的Valentino钱包!它的设计简直太精致了,每一个细节都展现着高级感和品质。钱包的材质非常优质,手感极佳,让人爱不释手。它有多种颜色可选,每一种都美到让人窒息!无论搭配什么风格的服装,都能成为亮点✨。内部空间设计合理,可以轻松容纳各种卡片和现金,非常实用。拥有Valentino钱包,就像是拥有了一份独特的时尚态度,让你在人群中脱颖而出。Valentino钱包的设计堪称
- 2018-12-01
11bbc2c5d0c6
练习题1小明varscore=prompt('请输入小明的期末成绩(0-100):');if(score==100){alert('BMW');}elseif(score>=80&&score=60&&score练习题2嫁女儿varH=180,M=10000000,F=500;if(H>=180&&M>=10000000&&F>=500){alert('我一定要嫁给他');}elseif(H>=1
- 2018-12-13
1bdb7fe682ab
姓名:周贤文常州新日催化剂有限公司【日精进打卡第63天】【知~学习】1.《六项精进》1遍共94遍1.《大学》1遍共93遍【经典名句分享】创新的秘密在于知道如何把你的智谋藏而不露。——爱因斯坦喜欢(566)加入句集评论(2)浅浅梦分享人类的创新之举是极其困难的,因此便把已有的形式视为神圣的遗产。——蒙森【行~实践】一、修身:听音乐二、齐家:洗衣服【省~觉悟】说那么多干嘛,干就完了{积善}:从2018
- Python FastAPI 与传统 Web 框架的性能对比
Python编程之道
pythonfastapi前端ai
PythonFastAPI与传统Web框架的性能对比关键词:FastAPI、性能对比、Web框架、异步编程、Python、Django、Flask摘要:本文深入探讨了FastAPI与传统PythonWeb框架(如Django和Flask)在性能方面的差异。我们将从架构设计、请求处理模型、并发能力等多个维度进行对比分析,并通过基准测试数据展示实际性能差异。文章还将提供代码示例和性能优化建议,帮助开发
- 警方认定网红用濒危大白鲨做美食,网友神吐槽
赛鲁斯
“天必像烟云消散,地必如衣服渐渐旧了;其上的居民也要如此死亡。唯有我的救恩永远长存;我的公义也不废掉。”——圣经话说这两天“濒危物种”这个词频繁出现,前些日子是长江白鲟被确定灭绝,同时其它鲟鱼被列为及其濒危,之后有一位网络美食博主在视频里烧烤鲨鱼,被怀疑是国际濒危的大白鲨。据光明网报道,7月14日,一位名叫“提子”的美食网红博主拍摄水煮鲨鱼和烧烤鲨鱼的视频火爆网络,有科普博主反映,这条鲨鱼是国际濒
- Python Django 数据库索引优化
Python编程之道
pythondjango数据库ai
PythonDjango数据库索引优化关键词:DjangoORM、数据库索引、查询优化、性能调优、PostgreSQL、MySQL、执行计划摘要:本文深入探讨Django框架中的数据库索引优化策略。我们将从数据库索引的基本原理出发,详细分析DjangoORM如何生成SQL查询,以及如何通过合理的索引设计提升查询性能。文章包含索引类型选择、复合索引优化、Django模型字段索引配置、查询集优化技巧等
- Python Scrapy爬取办公用品网站数据的策略
Python编程之道
pythonscrapy开发语言ai
1.引入与连接想象一下,你是一家办公用品公司的市场调研人员,需要了解竞争对手的产品价格、种类等信息。如果手动去各个办公用品网站收集这些数据,那将是一项极其繁琐且耗时的工作。而Python的Scrapy框架就像是一个不知疲倦的超级助手,能帮你快速、高效地从众多网站抓取所需数据。你可能已经对Python有了一定的了解,知道它是一门功能强大且应用广泛的编程语言。Scrapy则是Python中专门用于网络
- 使用Python Scrapy打造个性化爬虫
使用PythonScrapy打造个性化爬虫——知识金字塔构建1.引入与连接:从“手动复制”到“自动化采集”的跨越你是否遇到过这样的场景?想整理1000条知乎优质回答做数据分析,却要逐条复制;想追踪某电商平台的商品价格波动,却要每天手动刷新页面……这些重复劳动,正是“个性化爬虫”的用武之地!与已有知识的连接:你可能用过requests+BeautifulSoup写过简单爬虫,但面对大规模数据、复杂反
- 劝你别瞎自学!2025AI大模型路线图,手把手教你!大模型新人必看,少走三年弯路就靠这篇!
AGI大模型老王
人工智能程序员chatgptAI产品经理大模型AI大模型学习
这两年,大模型从实验室里的高冷研究,走到每个程序员、学生、转行者的聊天框和职业规划表里。几乎每天都有人来问我:"师兄,我是做后端的,能不能转大模型?""我在看一些课程,不知道该学哪些才有用?""我试着搭了个模型,发现全是坑,是不是我不适合?"今天这篇文章,我不打算讲那些泛泛而谈的大模型原理,我就站在一个“老转行人+老程序员+老训练营主理人”的角度,跟你聊聊:大模型怎么转?适合哪些人?哪些方向对新手
- 《聚宝盆成精后,我抢了个古代男友》叶苜苜战承胤
一米文库
简介:父母死后,叶苜苜一直浑浑噩噩,并没有第一时间察觉,家里会莫名其妙多些东西。譬如:有时是黄纸,纸张繁体字写关于战争、干旱、饥荒的事迹。有时是半个旧瓷碗的碎片。有次家里突然出现带血的断刀片。她才恍然惊觉,一度以为家里闹了鬼!书名:《聚宝盆成精后,我抢了个古代男友》主角:叶苜苜战承胤类型:现代言情打开微信搜索公众号-【一米文库】关注并回复数字:2013即可快速免费阅读《聚宝盆成精后,我抢了个古代男
- 强大的销售团队背后 竟然是大数据分析的身影
蓝儿唯美
数据分析
Mark Roberge是HubSpot的首席财务官,在招聘销售职位时使用了大量数据分析。但是科技并没有挤走直觉。
大家都知道数理学家实际上已经渗透到了各行各业。这些热衷数据的人们通过处理数据理解商业流程的各个方面,以重组弱点,增强优势。
Mark Roberge是美国HubSpot公司的首席财务官,HubSpot公司在构架集客营销现象方面出过一份力——因此他也是一位数理学家。他使用数据分析
- Haproxy+Keepalived高可用双机单活
bylijinnan
负载均衡keepalivedhaproxy高可用
我们的应用MyApp不支持集群,但要求双机单活(两台机器:master和slave):
1.正常情况下,只有master启动MyApp并提供服务
2.当master发生故障时,slave自动启动本机的MyApp,同时虚拟IP漂移至slave,保持对外提供服务的IP和端口不变
F5据说也能满足上面的需求,但F5的通常用法都是双机双活,单活的话还没研究过
服务器资源
10.7
- eclipse编辑器中文乱码问题解决
0624chenhong
eclipse乱码
使用Eclipse编辑文件经常出现中文乱码或者文件中有中文不能保存的问题,Eclipse提供了灵活的设置文件编码格式的选项,我们可以通过设置编码 格式解决乱码问题。在Eclipse可以从几个层面设置编码格式:Workspace、Project、Content Type、File
本文以Eclipse 3.3(英文)为例加以说明:
1. 设置Workspace的编码格式:
Windows-&g
- 基础篇--resources资源
不懂事的小屁孩
android
最近一直在做java开发,偶尔敲点android代码,突然发现有些基础给忘记了,今天用半天时间温顾一下resources的资源。
String.xml 字符串资源 涉及国际化问题
http://www.2cto.com/kf/201302/190394.html
string-array
- 接上篇补上window平台自动上传证书文件的批处理问卷
酷的飞上天空
window
@echo off
: host=服务器证书域名或ip,需要和部署时服务器的域名或ip一致 ou=公司名称, o=公司名称
set host=localhost
set ou=localhost
set o=localhost
set password=123456
set validity=3650
set salias=s
- 企业物联网大潮涌动:如何做好准备?
蓝儿唯美
企业
物联网的可能性也许是无限的。要找出架构师可以做好准备的领域然后利用日益连接的世界。
尽管物联网(IoT)还很新,企业架构师现在也应该为一个连接更加紧密的未来做好计划,而不是跟上闸门被打开后的集成挑战。“问题不在于物联网正在进入哪些领域,而是哪些地方物联网没有在企业推进,” Gartner研究总监Mike Walker说。
Gartner预测到2020年物联网设备安装量将达260亿,这些设备在全
- spring学习——数据库(mybatis持久化框架配置)
a-john
mybatis
Spring提供了一组数据访问框架,集成了多种数据访问技术。无论是JDBC,iBATIS(mybatis)还是Hibernate,Spring都能够帮助消除持久化代码中单调枯燥的数据访问逻辑。可以依赖Spring来处理底层的数据访问。
mybatis是一种Spring持久化框架,要使用mybatis,就要做好相应的配置:
1,配置数据源。有很多数据源可以选择,如:DBCP,JDBC,aliba
- Java静态代理、动态代理实例
aijuans
Java静态代理
采用Java代理模式,代理类通过调用委托类对象的方法,来提供特定的服务。委托类需要实现一个业务接口,代理类返回委托类的实例接口对象。
按照代理类的创建时期,可以分为:静态代理和动态代理。
所谓静态代理: 指程序员创建好代理类,编译时直接生成代理类的字节码文件。
所谓动态代理: 在程序运行时,通过反射机制动态生成代理类。
一、静态代理类实例:
1、Serivce.ja
- Struts1与Struts2的12点区别
asia007
Struts1与Struts2
1) 在Action实现类方面的对比:Struts 1要求Action类继承一个抽象基类;Struts 1的一个具体问题是使用抽象类编程而不是接口。Struts 2 Action类可以实现一个Action接口,也可以实现其他接口,使可选和定制的服务成为可能。Struts 2提供一个ActionSupport基类去实现常用的接口。即使Action接口不是必须实现的,只有一个包含execute方法的P
- 初学者要多看看帮助文档 不要用js来写Jquery的代码
百合不是茶
jqueryjs
解析json数据的时候需要将解析的数据写到文本框中, 出现了用js来写Jquery代码的问题;
1, JQuery的赋值 有问题
代码如下: data.username 表示的是: 网易
$("#use
- 经理怎么和员工搞好关系和信任
bijian1013
团队项目管理管理
产品经理应该有坚实的专业基础,这里的基础包括产品方向和产品策略的把握,包括设计,也包括对技术的理解和见识,对运营和市场的敏感,以及良好的沟通和协作能力。换言之,既然是产品经理,整个产品的方方面面都应该能摸得出门道。这也不懂那也不懂,如何让人信服?如何让自己懂?就是不断学习,不仅仅从书本中,更从平时和各种角色的沟通
- 如何为rich:tree不同类型节点设置右键菜单
sunjing
contextMenutreeRichfaces
组合使用target和targetSelector就可以啦,如下: <rich:tree id="ruleTree" value="#{treeAction.ruleTree}" var="node" nodeType="#{node.type}"
selectionChangeListener=&qu
- 【Redis二】Redis2.8.17搭建主从复制环境
bit1129
redis
开始使用Redis2.8.17
Redis第一篇在Redis2.4.5上搭建主从复制环境,对它的主从复制的工作机制,真正的惊呆了。不知道Redis2.8.17的主从复制机制是怎样的,Redis到了2.4.5这个版本,主从复制还做成那样,Impossible is nothing! 本篇把主从复制环境再搭一遍看看效果,这次在Unbuntu上用官方支持的版本。 Ubuntu上安装Red
- JSONObject转换JSON--将Date转换为指定格式
白糖_
JSONObject
项目中,经常会用JSONObject插件将JavaBean或List<JavaBean>转换为JSON格式的字符串,而JavaBean的属性有时候会有java.util.Date这个类型的时间对象,这时JSONObject默认会将Date属性转换成这样的格式:
{"nanos":0,"time":-27076233600000,
- JavaScript语言精粹读书笔记
braveCS
JavaScript
【经典用法】:
//①定义新方法
Function .prototype.method=function(name, func){
this.prototype[name]=func;
return this;
}
//②给Object增加一个create方法,这个方法创建一个使用原对
- 编程之美-找符合条件的整数 用字符串来表示大整数避免溢出
bylijinnan
编程之美
import java.util.LinkedList;
public class FindInteger {
/**
* 编程之美 找符合条件的整数 用字符串来表示大整数避免溢出
* 题目:任意给定一个正整数N,求一个最小的正整数M(M>1),使得N*M的十进制表示形式里只含有1和0
*
* 假设当前正在搜索由0,1组成的K位十进制数
- 读书笔记
chengxuyuancsdn
读书笔记
1、Struts访问资源
2、把静态参数传递给一个动作
3、<result>type属性
4、s:iterator、s:if c:forEach
5、StringBuilder和StringBuffer
6、spring配置拦截器
1、访问资源
(1)通过ServletActionContext对象和实现ServletContextAware,ServletReque
- [通讯与电力]光网城市建设的一些问题
comsci
问题
信号防护的问题,前面已经说过了,这里要说光网交换机与市电保障的关系
我们过去用的ADSL线路,因为是电话线,在小区和街道电力中断的情况下,只要在家里用笔记本电脑+蓄电池,连接ADSL,同样可以上网........
- oracle 空间RESUMABLE
daizj
oracle空间不足RESUMABLE错误挂起
空间RESUMABLE操作 转
Oracle从9i开始引入这个功能,当出现空间不足等相关的错误时,Oracle可以不是马上返回错误信息,并回滚当前的操作,而是将操作挂起,直到挂起时间超过RESUMABLE TIMEOUT,或者空间不足的错误被解决。
这一篇简单介绍空间RESUMABLE的例子。
第一次碰到这个特性是在一次安装9i数据库的过程中,在利用D
- 重构第一次写的线程池
dieslrae
线程池 python
最近没有什么学习欲望,修改之前的线程池的计划一直搁置,这几天比较闲,还是做了一次重构,由之前的2个类拆分为现在的4个类.
1、首先是工作线程类:TaskThread,此类为一个工作线程,用于完成一个工作任务,提供等待(wait),继续(proceed),绑定任务(bindTask)等方法
#!/usr/bin/env python
# -*- coding:utf8 -*-
- C语言学习六指针
dcj3sjt126com
c
初识指针,简单示例程序:
/*
指针就是地址,地址就是指针
地址就是内存单元的编号
指针变量是存放地址的变量
指针和指针变量是两个不同的概念
但是要注意: 通常我们叙述时会把指针变量简称为指针,实际它们含义并不一样
*/
# include <stdio.h>
int main(void)
{
int * p; // p是变量的名字, int *
- yii2 beforeSave afterSave beforeDelete
dcj3sjt126com
delete
public function afterSave($insert, $changedAttributes)
{
parent::afterSave($insert, $changedAttributes);
if($insert) {
//这里是新增数据
} else {
//这里是更新数据
}
}
- timertask
shuizhaosi888
timertask
java.util.Timer timer = new java.util.Timer(true);
// true 说明这个timer以daemon方式运行(优先级低,
// 程序结束timer也自动结束),注意,javax.swing
// 包中也有一个Timer类,如果import中用到swing包,
// 要注意名字的冲突。
TimerTask task = new
- Spring Security(13)——session管理
234390216
sessionSpring Security攻击保护超时
session管理
目录
1.1 检测session超时
1.2 concurrency-control
1.3 session 固定攻击保护
- 公司项目NODEJS实践0.3[ mongo / session ...]
逐行分析JS源代码
mongodbsessionnodejs
http://www.upopen.cn
一、前言
书接上回,我们搭建了WEB服务端路由、模板等功能,完成了register 通过ajax与后端的通信,今天主要完成数据与mongodb的存取,实现注册 / 登录 /
- pojo.vo.po.domain区别
LiaoJuncai
javaVOPOJOjavabeandomain
POJO = "Plain Old Java Object",是MartinFowler等发明的一个术语,用来表示普通的Java对象,不是JavaBean, EntityBean 或者 SessionBean。POJO不但当任何特殊的角色,也不实现任何特殊的Java框架的接口如,EJB, JDBC等等。
即POJO是一个简单的普通的Java对象,它包含业务逻辑
- Windows Error Code
OhMyCC
windows
0 操作成功完成.
1 功能错误.
2 系统找不到指定的文件.
3 系统找不到指定的路径.
4 系统无法打开文件.
5 拒绝访问.
6 句柄无效.
7 存储控制块被损坏.
8 存储空间不足, 无法处理此命令.
9 存储控制块地址无效.
10 环境错误.
11 试图加载格式错误的程序.
12 访问码无效.
13 数据无效.
14 存储器不足, 无法完成此操作.
15 系
- 在storm集群环境下发布Topology
roadrunners
集群stormtopologyspoutbolt
storm的topology设计和开发就略过了。本章主要来说说如何在storm的集群环境中,通过storm的管理命令来发布和管理集群中的topology。
1、打包
打包插件是使用maven提供的maven-shade-plugin,详细见maven-shade-plugin。
<plugin>
<groupId>org.apache.maven.
- 为什么不允许代码里出现“魔数”
tomcat_oracle
java
在一个新项目中,我最先做的事情之一,就是建立使用诸如Checkstyle和Findbugs之类工具的准则。目的是制定一些代码规范,以及避免通过静态代码分析就能够检测到的bug。 迟早会有人给出案例说这样太离谱了。其中的一个案例是Checkstyle的魔数检查。它会对任何没有定义常量就使用的数字字面量给出警告,除了-1、0、1和2。 很多开发者在这个检查方面都有问题,这可以从结果
- zoj 3511 Cake Robbery(线段树)
阿尔萨斯
线段树
题目链接:zoj 3511 Cake Robbery
题目大意:就是有一个N边形的蛋糕,切M刀,从中挑选一块边数最多的,保证没有两条边重叠。
解题思路:有多少个顶点即为有多少条边,所以直接按照切刀切掉点的个数排序,然后用线段树维护剩下的还有哪些点。
#include <cstdio>
#include <cstring>
#include <vector&