人工智能学习（三）：通过搜索进行问题求解——有信息搜索
目录
引言
2.1 贪婪最佳优先搜索
2.2 贪婪最佳优先搜索 V.S. 一致代价搜索
2.3 A*搜索：缩小总评估代价
2.4 A*搜索和一致代价搜索的直观比较
2.5 五种搜索算法的直观比较
2.6 可接受的启发式方法
2.7 局部搜索算法
2.7.1 局部搜索算法
2.7.2 爬山算法
引言
有信息搜索又称为启发式搜索：
使用问题本身的定义之外的特定知识——比无信息的搜索策略更有效地进行问题求解。
最佳优先搜索（best-first search）：
我们要考虑的一般算法称为最佳优先搜索。 最佳优先搜索结点是基于评价函数
值被选择扩展的。评估函数被看作是代价估计，因此评估值最低的结点被选择首先进行扩展。
最佳优先图搜索的实现与一致代价搜索类似，不过最佳优先是根据
值而不是
值对优先级队列排队。
启发函数（heuristic function）：
对
结点
到目标结点的最小代价路径的代价估计值
（要注意的是
以结点为输入，但它与
不同，它只依赖于结点状态）。
若n是目标结点，则
。
启发式函数常用的测距方法：
曼哈顿距离
两点之间沿着坐标轴方向的累积距离
欧几里得距离
两点之间的直线距离
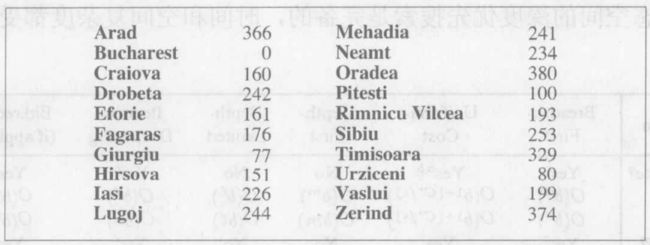
描述一下下面使用的问题情景：
在地图中寻找起始城市到达目标城市的路径。如未指明，起始城市默认为：
；目标城市默认为：
。
启发式函数默认使用直线距离：
2.1 贪婪最佳优先搜索
贪婪最佳优先搜索（greedy best-first search）：
贪婪最佳优先搜索试图扩展离目标最近的结点，理由是这样可能可以很快找到解。
启发函数：
只用启发式信息，即
。
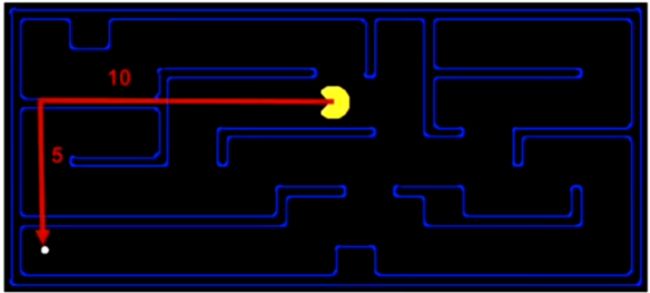
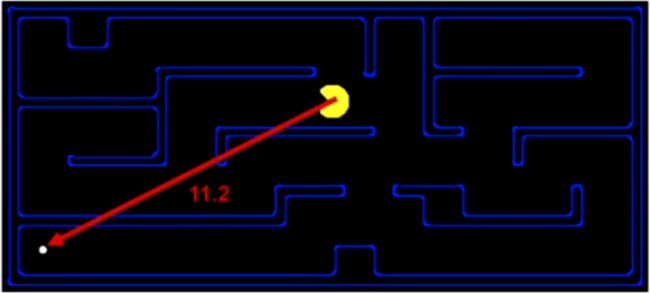
将此算法应用在罗马尼亚问题中；使用直线距离启发式，记为
。 如果目的地是，我们需要知道到达的直线距离，如图所示。不能由问题本身的描述计算得到。而且，由经验可知和实际路程相关，因此这是一个有用的启发式。
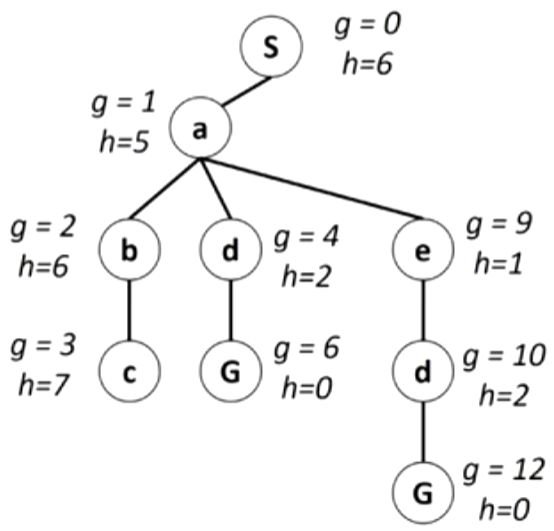
下图给出了使用的贪婪最佳优先搜索寻找从到的路的过程：
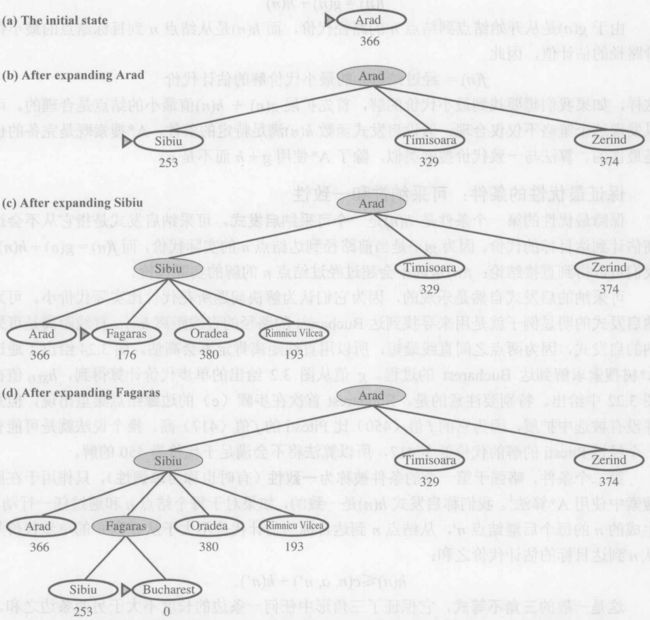
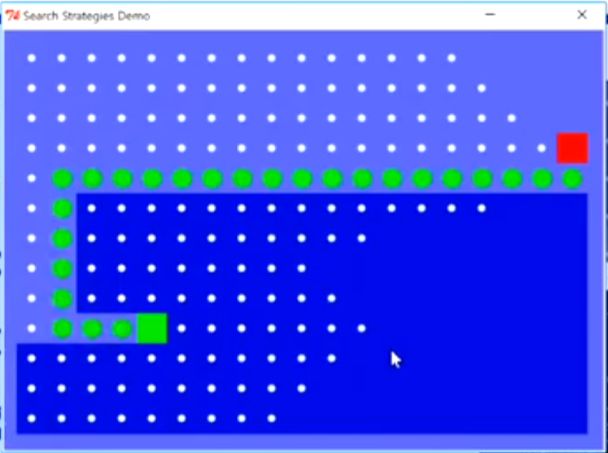
- 从出发最先扩展
，因为与
和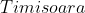
相比，它距离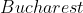最近。 - 下一个扩展的结点是
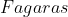，因为它是离目标最近的。 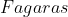- 接下来生成了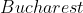，也就是目标结点。
完备性：贪婪最佳优先搜索不是完备的。
贪婪最佳优先搜索与深度优先搜索类似，即使是有限状态空间，它也是不完备的。考虑从
到
理想状态下，启发式建议先扩展
，因为它离
——根据启发式这是离目标较远的一步，然后继续前往
，
然而，算法始终找不到这个解，因为扩展
最优性：贪婪最佳优先搜索不是最优的。
对于这个特殊问题，使用
到
到
公里。这说明了为什么这个算法被称为“贪婪的”——在每一步它都要试图找到离目标最近的结点。
最坏情况下，时间和空间复杂度都是
，其中
是搜索空间的最大深度。然而这是建立在启发式函数是直线距离的基础上，如果有一个好的启发式函数，复杂度可以得到有效降低。下降的幅度取决于特定的问题和启发式函数的质量。
时间复杂度：最坏情况下，算法的时间复杂度为
空间复杂度：最坏情况下，算法的空间复杂度为
2.2 贪婪最佳优先搜索 V.S. 一致代价搜索
我们上一篇博客学习了一直代价搜索，一致代价搜索主张扩展
最小的节点，它和贪婪最佳优先搜索的区别和联系是什么呢？
如果把
比喻成一只乌龟，缓慢的、按部就班地依次对所有当前最短的进行搜索，但它是完备的并且最终得到最优解。
贪婪最佳优先搜索就是兔子，跑的很快，但是不一定找到最优解甚至不一定完备。
下面有一个例子：左边是各个
的状态图，右边是根据状态图构建的搜索树。
对于这样一颗搜索树，其中是从起始节点到当前边缘节点的累积；如果按照的思路，会依次扩展
然，得到最优解。
如果对于贪婪最佳优先搜索，则依据的是当前边缘节点到目标节点的距离，然后选择最短的一条，因此他会依次扩展：
，很显然，这并不是最优的。
2.3 A*搜索：缩小总评估代价
最佳优先搜索的最广为人知的形式是
搜索。搜索结合了贪婪最佳优先搜索和的优点。
启发函数：
它对结点的评估结合了
由于
经过结点n的最小代价解的估计代价
注意：将节点压入边缘节点集合的时候如果符合目标检测的条件，搜索不能马上结
束。而应该等到这个边缘节点从数据结构中弹出才能进行目标检测判断是否结束。
目标检测时机：
目标检测应用于结点被选择扩展时，而不是在结点生成的时候进行。
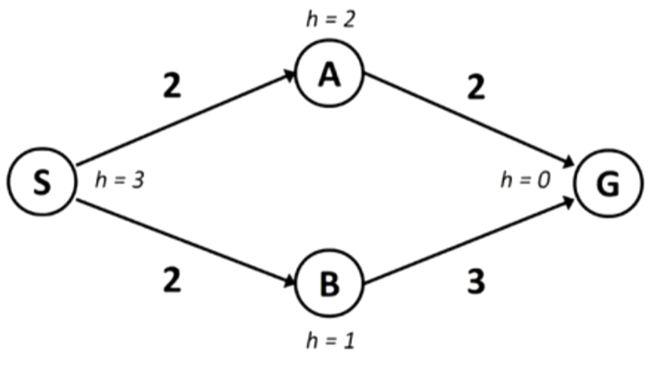
这是为什么呢？我们描述一个应用场景：
在本图中，首先扩展
，边缘节点集合中加入
，根据的
：
得出应该扩展
；这个时候边缘节点集合更新为
。如果这时候仅凭
是否出现在边缘节点集合中判断是否返回，那么现在就得到了
这条路，
，显然不是最优路径；
按照规定的流程，比较和
哪个应该被扩展，此时的
；的
，因此应该选择 进行扩展，而这时候边缘节点集合更新为
；从那边到达的的，因此应该选择扩展
，
，是最优路径。
具体描述：
- 首先扩展。
- 扩展
，现在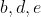
作为边缘节点。 - 根据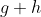最小选择作为新的扩展节点进行扩展，边缘节点集中的节点更新为：
。 - 对进行扩展（加入到解中），进行目标检测，程序结束。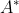搜索算法完成。
这样，如果我们想要找到最小代价的解，首先扩展
值最小的结点是合理的。可以发现这个策略不仅仅合理：假设启发式函数满足特定的条件，搜索既是完备的也是最优的。算法与一致代价搜索类似，除了使用而不只是。
完备性：
最优性：
但是存在保证最优性的条件——可采纳性和一致性：
可采纳性：
因为
。我们可以得到直接结论：
可采纳的启发式自然是乐观的，因为它们认为解决问题所花代价比实际代价小。
一致性：
只作用于在图搜索中使用
，从结点
这是一般的三角不等式，它保证了三角形中任何一条边的长度不大于另两条边之和。这里，三角形是由
构成的。
对于可采纳的启发式，这种不等式有明确意义：如果从
时间复杂度：最坏情况下，算法的时间复杂度为。
空间复杂度：最坏情况下，算法的空间复杂度为。
证明可采纳性是搜索是最优性的条件：
上面说到只要
，由于没有过高地估计某个点到目标点的花费，这样我们必然能够找到最优的线路；而相反，如果某个点的
，那么我们就很有可能不会走这个点。
下面给出一个形式化的证明：
我们假设出发点位于顶端，为最优目标点，为非最优目标点，为最优线路上的点：
因为是某条线路下的目标点
所以
，同理
又因为非最优目标点，为最优目标点
所以
，
，对于点来说，
所以
而我们知道为最优目标点，故
综上
所以永远也不会通过走某条非最优路来到达目标点！
2.4 A*搜索和一致代价搜索的直观比较
UCS
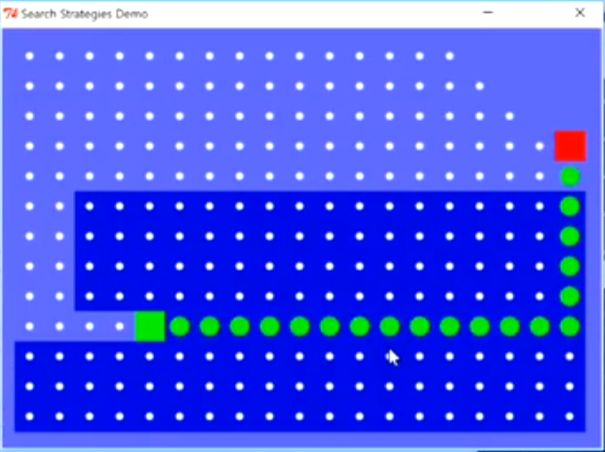
UCS的吃豆人
虽然和有着类似的扩散，但是更倾向于靠近目标点，向有利于目标的方向扩散。
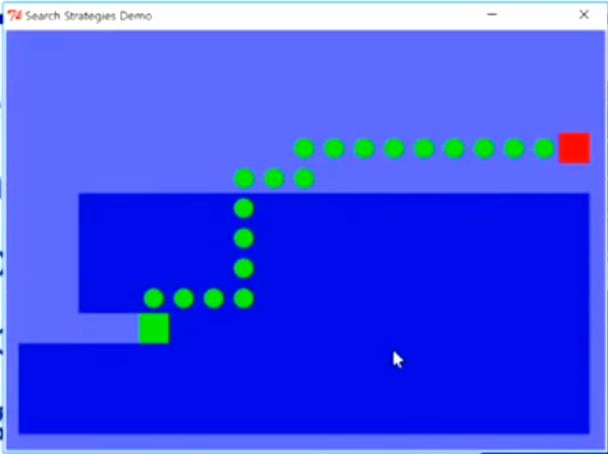
A星搜索的吃豆人
Greedy
2.5 五种搜索算法的直观比较
BFS
DFS
Greedy
UCS
2.6 可接受的启发式方法
主导：
那么
就会支配
，并且更有利于搜索。
在保证启发式是可接受的范围内，越接近真实的距离，越节省计算量。
宽松问题（Relaxed problems）：
可接受的启发式方法可以从问题的宽松版本的精确解决成本中得出。
如果8拼图的规则被放宽，使瓷砖可以移动到任何地方，那么给出了最短的解决方案。
如果放宽规则，使瓷砖可以移动到任何相邻的方格，那么给出了最短的解决方案。
2.7 局部搜索算法
参考：爬山算法
2.7.1 局部搜索算法
例如我们上面所提到的所有案例，都返回从初始状态到目标状态的这条路径作为这个问题的解；
而实际中有很多最优化的问题，不关心路径，它只关心状态本身，它需要算法找到一个符合要求的目标状态，那么这个目标状态本身才是问题的解。针对这一类问题我们可以采用局部搜索算法。
局部搜索算法不记录它的搜索过程，它只记录一个或多个当前状态，然后通过不断的改进修改当前状态，直到它满足目标约束，也就是说是一个目标状态为止。那么这个目标状态本身返回去作为这个问题的解，那么它叫做局部的原因就是因为它只储存当前状态。那么它并不像前面一样，系统的记录从初始结点到达后续结点、目标节点的路径，并不储存这些东西。它只是在当前状态这个局部领域里记录它的搜索。这个是局部搜索算法的思想和它适用的问题。
这种算法有一个很大的优点，就是它对存储空间的要求非常的低，它只需要存储当前状态，并不需要把它走过的结点都记录下来。所以它对于现实世界的问题，一般都是无限空间状态的问题。那么它是很有实用性的，也就是说它可以用来解决一些实际的大问题。
2.7.2 爬山算法
那么首先我们来看到第一种局部搜索算法叫做爬山搜索，爬山搜索就是不断地向更高点前进。
爬山搜索就像有失忆的人在浓雾中攀登珠峰。这句话就是很形象的比喻出来了爬山搜索算法的两个问题：
失忆的人，那么他是不记得他曾经到过什么地方，也就是说它只记得它自己现在处在什么位置，周边是什么样的。——只储存当前状态
浓雾中攀登珠峰，在浓雾中定就是看的不远。他只能看到他周边的地形，远处如果有更高的山峰他是看不到的。——只把局部的最值点返回
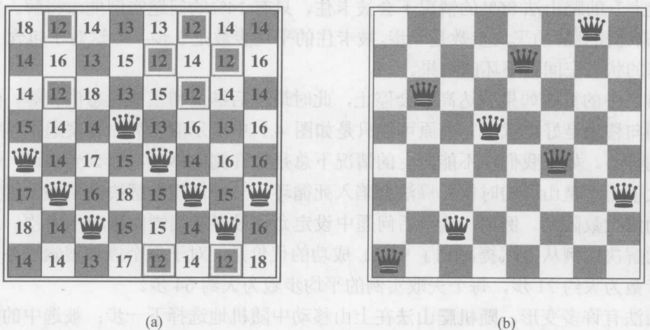
例子：
互相攻击到的皇后对数
虽然不是一个正确的解，但他是爬山法得出的一个局部最优解，
。