3 AI 经典搜索算法知识点

3.1 Problem solving in AI 人工智能中的问题求解

• The solution 解
  It is a sequence of actions to reach the goal.
  解是一个达到目标的动作序列。
• search 搜索
  The process of looking for a sequence of actions that reaches the goal is called search. (The process of looking for a solution)
  为达到目标，寻找这样的行动序列的过程被称为搜索。
• A search algorithm takes a problem as input and returns a solution in the form of an action sequence.
  搜索算法的输入是问题，输出是问题的解，以行动序列的形式返回问题的解。
• State space 状态空间
  The state space of the problem is formally defined by: initial state, actions and goal state.
  问题的状态空间可以形式化地定义为：初始状态、动作（操作）和目标状态。
• Goal test is to determine whether a given state is a goal state.
  目标测试，确定给定的状态是不是目标状态.
• Graph 图
  State space forms a graph, in which nodes are states, and links are actions.
  状态空间形成一个图，其中节点表示状态、链接表示动作。
• Path 路径
  A path in the state space is a sequence of states connected by a sequence of actions. 状态空间的一条路径是通过行动连接起来的一个状态序列。
• Path cost 路径代价
  Assign a numeric value to each path to denote the cost of taking the action. The
  path cost can be described as the sum of the costs of the individual actions along the path.为每条路径赋一个代价值，即边加权。一条路径的代价值为该路径上的每个行动（每条边）的耗散值总和。
• 人工智能研究的搜索技术问题：
  如何生成、存储与问题有关的部分状态空间？
• 知识存储方式：
  显示存储：与问题有关的全部知识（叙述知识、过程知识和控制知识）都存入知识库。
  隐式存储：只存储与问题求解有关部分知识。
  在知识库种存储局部状态空间图
  从初始状态出发，运用相应知识生成部分状态空间图，通过搜索逐步达到目标状态。
• 为了节约存储容量，提高存储效率，采用隐式存储，进行隐式图搜索。

3.2 Example

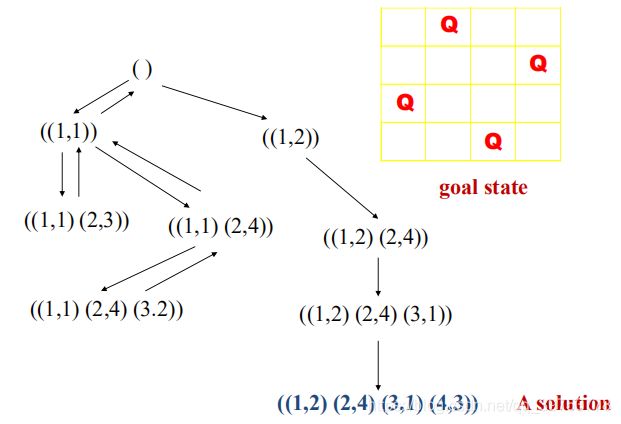
Problem 1: 8-queens problem

The goal is to place 8 queens on a chessboard such that no queen attacks any other. (A queen attacks any piece in the same row, column or diagonal.)
八皇后问题的目标是将8个皇后摆放在国际象棋的棋盘上，使得皇后之间不发生攻击一个皇后会攻击同一行、同一列或同一斜线上的其他皇后）。

In figure ©, the queen in the rightmost column is attacked by the queen at the top left.最右下角的皇后与最左上角的皇后可能互相攻击。

• States: Any arrangement of 0 to 8 queens on the board is a state.
  棋盘上0 到8 个皇后的任一摆放都是一个状态。
• Initial state: No queens on the board.棋盘上没有皇后。
• Actions: Add a queen to any empty square. 在任一空格增加摆放1 个皇后。
• Goal test: 8 queens are on the board, none attacked.
  8 个皇后都在棋盘上，并且不互相攻击。

Problem 2: 8-puzzle 8数码难题

• 3×3 board with 8 numbered tiles and a blank space.
  3×3棋盘上有8个数字棋子和一个空位。
• A tile adjacent to the blank space can slide into the space. The object is to reach a specified goal state， such as the one shown on the right of the figure (b）.与空位相邻的滑块可以移向该空位。游戏目标是达到一个指定的目标状态。
  
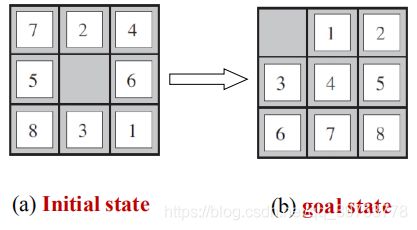
• States: A state description specifies the location of each of the eight tiles and the blank in one of the nine squares.状态描述指明8 个棋子以及空位在棋盘9 个方格上的分布。
• Initial state: Any state can be designated as the initial state.
  任何状态都可能是初始状态。
• Actions: defines the actions as movements of the blank space Left, Right, Up, or Down. It is equivalent to move a numbered tile into the blank space.
  动作：就是将空位向Left、Right、Up或Down 方向移动，等价于将数字牌移动到空位。
• Goal test: This checks whether the state matches the specified goal configuration
  目标测试：用来检测状态是否能匹配指定的目标布局.
• Path cost: Each step costs 1, so the path cost is the number of steps in the path.路径代价：每一步的代价值为1, 因此整个路径的代价值是路径中的步数。

Searching for Solutions 搜索解

• How to find the solutions of the problems?
  There are several methods （deduction 演绎，induction 归纳，reasoning 推理，searching 搜索）to solve the problems, but we focus on search algorithms.
• There are two types of searching:

Uninformed Search Strategies 无信息搜索策略（盲目搜索）	Informed Search Strategies 有信息搜索策略（启发式heuristic)
The strategies use only the information available in the problem definition. 只使用问题定义中可用的信息。	The strategies use problem-specific knowledge beyond the definition of the problem itself, so that can find solutions more efficiently than can an uninformed strategy.这类策略采用超出问题本身定义的、问题特有的知识(启发函数)，因此能够找到比无信息搜索更有效的解

• Uninformed Search Strategies 无信息搜索策略（盲目搜索）
   Backtracking search 回溯搜索
   Graph Search 图搜索

（1）General Graph Search 一般的图搜索
（2）Breadth-first search 宽度优先搜索
（3）Depth-first search 深度优先搜索
（4）Uniform-cost search 一致代价搜索
（5）Depth-limited search 深度受限搜索
（6）Iterative deepening search 迭代加深的深度优先搜索
（7）Bidirectional Search 双向搜索

• Informed Search Strategies 有信息搜索策略（ heuristic ）
  Best-first Search 最佳优先搜索
  A Search
  A Search*
  Local search algorithms（局部搜索）

 Hill-climbing search（爬山搜索）
 Local beam search（局部束搜索）
 Simulated annealing search（模拟煺火搜索）
 Genetic algorithms（遗传算法）

3.3 Uninformed Search Strategies 无信息搜索策略

• The uninformed search is also called blind search.无信息搜索也被称为盲目搜索。
• The term (uninformed, or blind) means that the search strategies have no additional information about states beyond that provided in the problem definition.该术语（无信息、盲目的）意味着该搜索策略没有超出问题定义提供的状态之外的附加信息。
• Uninformed search strategies use only the information available in the problem definition. 无信息搜索策略只使用问题定义中可用的信息。
• All they can do is to generate successors and distinguish a goal state from a non-goal state.搜索算法要做的就是生成后继结点，并且区分目标状态和非目标状态。
• All search strategies are distinguished by the order in which nodes are expanded.所有的搜索策略是由节点扩展的顺序加以区分。

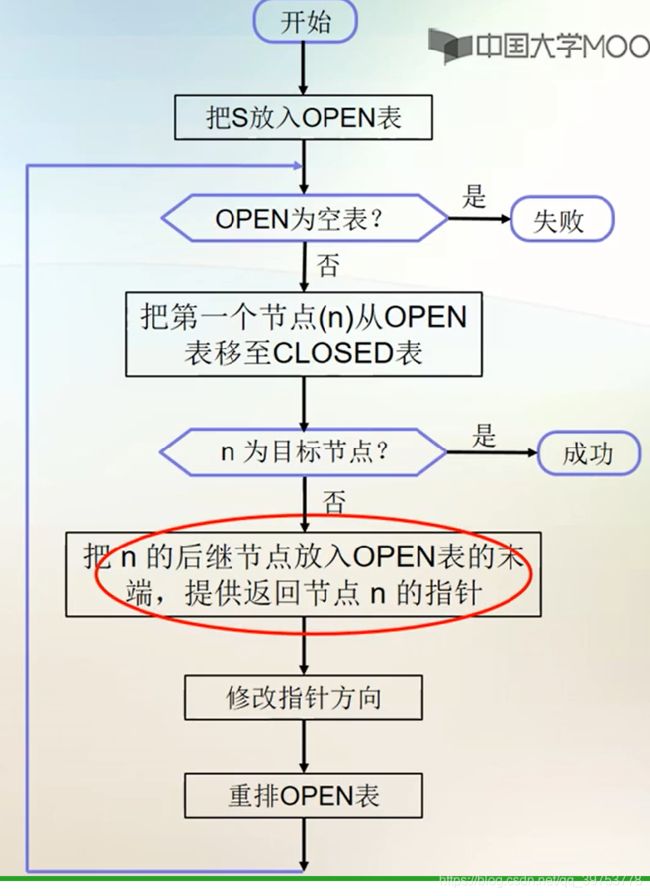
3.3.1 Backtracking search 回溯搜索

Backtracking search is as follows.

• Starting from the initial state, search for the path continuously and tentatively until it reaches the goal state or “unsolvable node”, that is, “dead end”.
  从初始状态出发，不停地、试探性地寻找路径，直到它到达目的状态或“不可解结
  点”，即“死胡同”为止。
• If it encounters an unsolvable node, it goes back to the nearest parent node in
  the path to see if there are any other child nodes that have not been expanded.
  若它遇到不可解结点，就回溯到路径中最近的父结点上，查看该结点是否还有其他的子结点未被扩展。
• If yes, the search continues along these child nodes;
  若有未被扩展的子结点，则沿这些子结点继续搜索；
• If it finds a goal state, exit the search successfully and return the problem–solving path. 如果找到目标状态，就成功退出搜索，返回解题路径。
  
• The number indicates the order in which the search is made.数字表示被搜索的次序.
• This procedure presents the property of recursive procedure.该过程呈现出递归过程的性质。

3.3.1 Backtracking Search Algorithm回溯搜索算法

Function BACKTRACK1（DATALIST）
DATALIST： is the state sequence from the initial state to the current state (reverse)
输入：从初始状态到当前状态的状态序列表（逆向）
returned value：a path from the current state to the goal state (expressed as a rule table, i.e. an action sequence) or FAIL
返回值:从当前状态到目标状态的路径（以规则表的形式表示）或FAIL。

1. DATA:=FIRST(DATALIST) 
2. // get the first state in the DATALIST
3. IF MENBER(DATA, TAIL(DATALIST)) // set element judgment 
	RETURN FAIL; // TAIL(DATALIST) remain the rest elements but the first
// if DATA is in TAIL(DATALIST), it means there is a loop. 出现回路，陷入死循环
4. IF TERM(DATA) RETURN NIL; // judge whether DATA is the goal state（终点）
5. IF DEADEND(DATA) RETURN FAIL; // judge whether DATA is the legal
6. IF LENGTH(DATALIST)>BOUND // judge if the recursive depth is too large
		RETURN FAIL; // if too deep, stop searching. Otherwise can not go back.
7. RULES:=APPRULES(DATA); // RULES is the set including all legal actions of the current state (DATA)，将DATA加入路径集合
8. LOOP: IF NULL(RULES) RETURN FAIL; // 判断动作集是否为空
9. R:=FIRST(RULES); // get the first action in the RULES 
10. RULES:=TAIL (RULES);
11. RDATA:=GEN (R, DATA);// 将动作R作用于当前状态，生成新状态
12. RDATALIST:=CONS (RDATA, DATALIST);// 将新状态加入到状态表中
13. PATH:=BACKTRCK1 (RDATALIST) // recursive call, 递归调用
14. IF PATH=FAIL GO LOOP;
15. RETURN CONS (R, PATH); // 将动作R加入到PATH中，并返回路径。

Example：4-Queens

Why need Graph Search

• A feature of the backtracking search strategy is that only one path from the initial state to the current state is recorded. When backtracking occurs, the search at the backtracking point will be “forgotten” by the algorithm. 回溯搜索策略的一个特点就是：只保留了从初始状态到当前状态的一条路径。当回溯出现时，回溯点处进行的搜索将被算法 “遗忘”。
• The advantage is that the storage space is saved; 其好处是节省了存储空间；
• The disadvantage is that these searched parts that have been forgotten can not be reused later. 其坏处是这些被回溯掉（遗忘掉）的已被搜索过的部分，以后无法使用。
• The graph search strategy records all the applied operations and their generated states in the search process. This search method is called “graph search” .图搜索策略则将搜索过程中所有应用过的操作及其生成的状态都记录下来，这种搜索方法称为“图搜索”
• Graph search has two advantages: 其优点有二：
  （1） The searched paths can be reused; 搜索过的路径可以被重复利用；
  （2） The knowledge related to the problem can be used more effectively to achieve the purpose of heuristic search. 可以更有效地利用与问题有关的知识，从而达到启发式搜索的目的。

耗费空间，节省时间

3.3.2 Graph Search 图搜索

（1）General Graph Search （GGS） 一般图搜索
（2）Breadth-first search 宽度优先搜索
（3）Depth-first search 深度优先搜索

Some Basic Concepts

• In a graph, a node denotes a state, an arc denotes an action.
• Depth of a node (结点深度)：
   Depth of the root (根结点深度)=0
   the Depth of the rest nodes = the Depth of its parent node+1
  其它结点深度=该结点的父结点深度+1
  
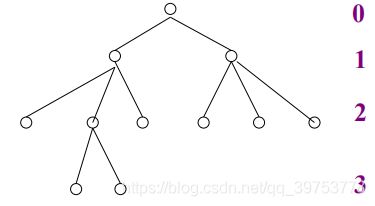
• Path （路径）
  Let a sequence of nodes be (n0, n1,…,nk) , for i=1,…,k. If node ni-1 has a
  successor node ni, the sequence is called a path from n0 to nk. 设一节点序列为(n0, n1,…,nk)，对于i=1,…,k，若节点ni-1具有一个后继节点ni，则该序列称为从n0到nk的路径。
• Path cost (路径代价)
  The cost of a path is equal to the sum of all the costs connected to each node of
  the path. g (n) represents the cost of a path from initial state to Node n.
  一条路径的代价等于连接这条路径各节点间所有代价的总和。用g(n)表示从初始状态到结点n的路径代价。
• Expand a node（扩展一个节点）
  All successor nodes of the node are generated and the cost of the connection arc is given. This process is called “Expand a node”.
  生成该结点的所有后继节点，并给出连接弧的代价。这一过程称为“扩展一个节点”。

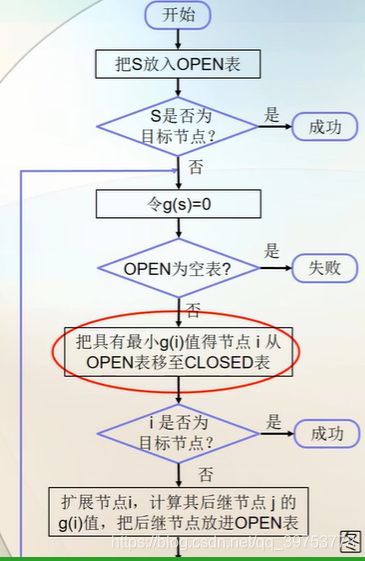
（1）General Graph Search Algorithm一般的图搜索算法

1. G=G0 (G0=s), OPEN:=(s);

// G is the generated search graph, Table OPEN is used for storing the nodes to be expanded, one node is taken out from Table OPEN to be expanded in each loop, and the newly generated nodes are added into Table OPEN ;
// G是生成的搜索图，OPEN表用来存储待扩展的结点，每次循环从OPEN表中取出一个结点加以扩展，并把新生成的结点加入OPEN表；

2. CLOSED:=( );

// Table CLOSED is used to store expanded nodes and is used to check whether newly generated nodes have been expanded. CLOSED表用来存储已扩展的结点，它的用途是检查新生成的结点是否已被扩展过。

3. LOOP: IF OPEN=( ) THEN EXIT(FAIL);
4. n:=FIRST(OPEN), REMOVE(n, OPEN), ADD(n, CLOSED);

// 将n从OPEN中删除，加入CLOSED中

5. IF GOAL(n) THEN EXIT(SUCCESS);
6. EXPAND(n)→{mi}, G:=ADD(mi, G);

// The set {mi} is established to include the successor nodes of n, but not the
ancestors of n, and these successor nodes are added to G.
// 扩展结点n，建立集合{mi}, 使其包含n的后继结点，而不包含n的祖先，并将这些后继结点加入G中。
Note：There are 3 types of n’s successor nodes ： {mi} = {mj} ∪ {mk} ∪ {ml},
（1）n’s successor mj is included neither in OPEN，nor in CLOSED；
（2） n’s successor mk is included in OPEN；
（3） n’s successor ml is included in CLOSED；
注：n 的后继结点有三类： {mi} = {mj} ∪ {mk} ∪ {ml},
（1）n的后继结点mj 既不包含于OPEN，也不包含于CLOSED；
（2）n的后继结点mk包含在OPEN中；
（3）n的后继结点ml 包含在CLOSED中；

7. For all nodes in {mi}, mark and modify their pointers.

//对{mi}中所有结点，标记和修改指针：

(1) ADD(mj, OPEN), and set a pointer from mj to n;

//并标记从mj到n的指针；

(2) judge whether the pointers of mk or ml should be set to point to n;

// 计算是否要修改 mk 和 ml 到n的指针，决定是否应当将它们的指针指向n（这些结点已有指针）；

(3) judge whether the pointers of the successors of ml should be set to point to ml;

// 计算是否要修改ml后继节点的指针，决定是否应当使ml的后继的指针指向ml 本身；

8. Reorder nodes in OPEN by some principle;

//对OPEN中的结点按某种原则重新排序；

9. GO LOOP；

GGS：Example of step 7(2)—Node 6

(a) To expand Node 6 (n=6), first generate its successor set {4,7}, where Node 4 is already in OPEN（only considering step 7(2)）, the cost of the original path {s➜3➜2➜4} is 5, the cost of the new path {S ➜6➜ 4} is 4, So the pointer of Node 4 should be changed from pointing to 2 to pointing to 6.
要扩展结点6，先生成其后继结点集合{4,7}，其中结点4已在OPEN中,只需考虑第7(2)步骤，原来路径{s➜3➜2➜4}代价为5，新路径{s➜6➜4}代价为4，故结点4的指针应由指向2改为指向6。
Dash line points from the current node to its previous node in the path.
Solid circle denotes the node in CLOSED, which is expanded already.
Hollow circle denotes the node in OPEN, which is waiting for being expanded.
GGS： Example of step 7(2) —Node 1

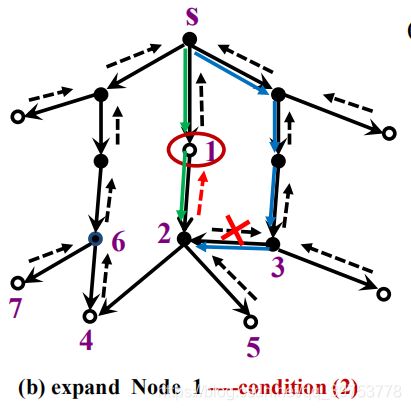
To expand Node 1 (n=1), first generate its successor set {2}, where Node 2 is already in CLOSED, so need to consider both Step 7(2) and 7(3).
要扩展结点1，先生成其后继结点集合{2}，结点2已在CLOSED中,需同时考虑 Step7中的(2)和 (3) 步骤.

• For Step 7(2), the cost of the original path {s➜3➜2} is 4, the cost of the new
  path {S ➜1➜ 2} is 2, So the pointer of Node 2 should be changed from pointing
  to 3 to pointing to 1.
  执行步骤7(2)，原来路径{s➜3➜2}代价为4，新路径{s➜1➜2}代价为2，故结点2的指针应由指向3改为指向1。
  GGS：Example of step 7(3) —Node 1
  
  © To expand Node 1, it has only one successor, Node 2, which is already in CLOSED.
• For Step 7(3), Node 2 has two successors (Node 4 and Node 5).
• There are two paths from S to Node 4: {S➜3➜2 ➜4} and {s➜6➜4}. The original pointer of Node 4 is to point to 6, whose cost is 4.
• Now we have a new new path {S ➜1➜ 2 ➜4}, its cost is 3, So the pointer of Node 4 should be changed from pointing to 6 to pointing to 2.
  执行步骤7(3)，结点2还有2个后继结点：4和5. 需要决定结点4和5的后继是否应改变指针。初始结点S到结点4已有两条路径：{S ➜3➜2 ➜4}和路径{s➜6➜4}, 代价分别为5和4. 结点4原来的指针指向6，其代价为4.现在从S到结点4又增加了一条新路径{s➜1➜2 ➜4},其代价为3，故© expand Node 1----condition (3) 结点4的指针应由指向6改为指向2。

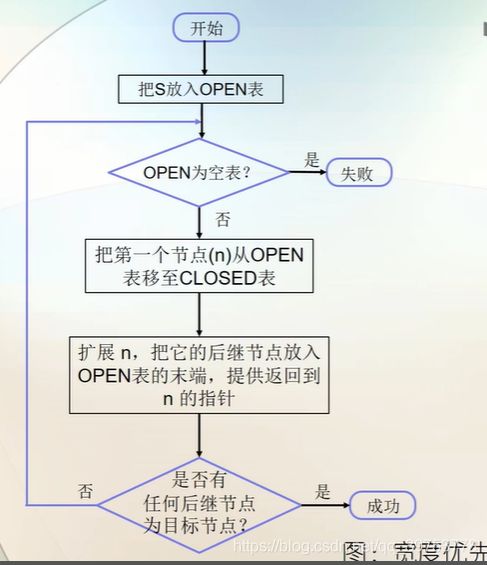
（2）Breadth-first Search 宽度优先搜索—BFS

• BFS is derived from a general graph search algorithm.
  BFS是从一般图搜索算法变化来的.
• BFS is to sort the nodes in Table OPEN in ascending order according to the node depth in the search tree. The nodes with the smallest depth are
  arranged at the front of Table OPEN, and the nodes with the same depth can be arranged in any arrangement. Such a search method is called “Breadth-first search”.
• BFS就是把OPEN表中的结点按搜索树中结点深度的增序排序，深度最小的结点排在最前面，深度相同的结点可以任意排列。这样的搜索方式称为“宽度优先搜索”。

Search Strategy 搜索策略

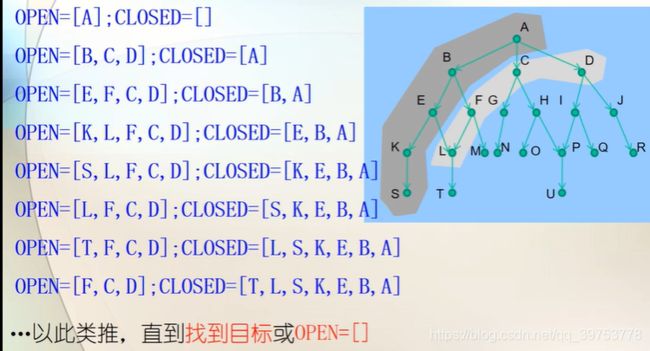
• It is a simple strategy in which the root node is expanded first, then all the successors of the root node are expanded next, then their successors, and so on. BFS是简单搜索策略. 先扩展根结点，接着扩展根结点的所有后继，然后再扩展它们的后继，依此类推。
• In BFS, the shallowest unexpanded node is chosen for expansion.
  BFS每次总是扩展深度最浅的结点。
• In general, all the nodes are expanded at a given depth in the search tree before any nodes at the next level are expanded.
  一般地，在下一层的任何结点扩展之前，搜索树上本层深度的所有结点都应该已经扩展过。

Implementation 实现方法

Use FIFO (First-In First-Out) queue to store Table OPEN.
使用FIFO队列存储OPEN表。
Thus, new nodes (which are always deeper than their parents) go to the tail of the queue, and old nodes, which are shallower than the new nodes, get expanded first.
新结点（结点比其父结点深）总是加入到队列尾端，这意味着浅层的老结点
会在深层的新结点之前被扩展。

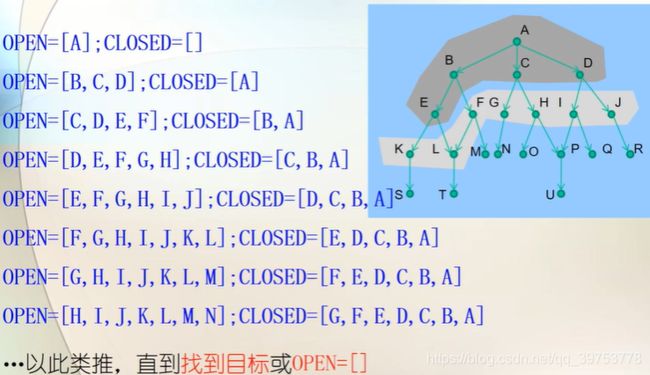
Breadth-first Search on a Simple Binary Tree 简单二叉树的宽度优先搜索

The searching order is {A, B, C, D, E, F, G}.

• The black circles denote expanded nodes.
  涂黑的圆圈表示已被扩展过的结点；
• The circle pointed by a triangle denote the node to be expanded next.
  三角指向的圆圈表示下一个将要被扩展的结点。

Breadth-First Search Algorithm

1. G:=G0 (G0=s), OPEN:=(s), CLOSED:=( );

// Table OPEN is used to store
the nodes to be expanded. OPEN is stored in a queue (FIFO) .

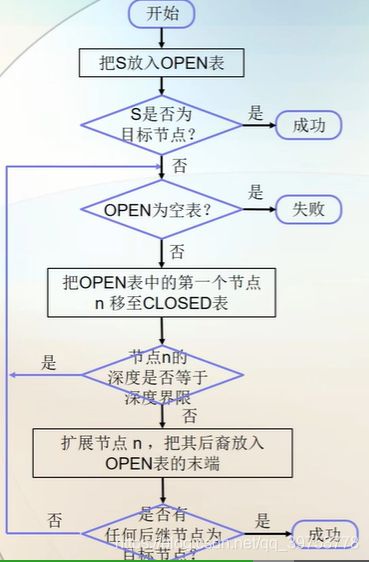
2. LOOP: IF OPEN=( ) THEN EXIT (FAIL);
3. n:=FIRST(OPEN);

//get the first element from Table OPEN(the front of queue)

4. IF GOAL(n) THEN EXIT (SUCCESS);
5. REMOVE(n, OPEN), ADD(n, CLOSED);
6. EXPAND(n) →{mi}, G:=ADD(mi, G);

// The set {mi} is established to include the successor nodes of n, but not the ancestors of n, and these successor nodes are added to G.
// 扩展结点n，建立集合{mi}, 使其包含n的后继结点，而不包含n的祖先，并将这些后继结点加入G中。

7. IF Goal state is in{mi}, THEN EXIT(SUCCESS);
8. ADD(mj,OPEN), and mark the pointer from mj to n;

// mj denotes the nodes that are neither in Table CLOSED nor in Table OPEN.
ADD is to place mj in the tail of Table OPEN, so that the shallowest nodes can
be expanded preferentially.
// mj表示不在CLOSED和OPEN中的结点，ADD用于把mj放进OPEN表尾端，使深度最浅的结点可优先扩展。

9. GO LOOP;
   

Features of BFS 宽度优先搜索的性质

• When the problem has a solution, it must be found.
  当问题有解时，一定能找到解.
• When the problem is unit cost and the problem has a solution, the optimal solution can be found. 当问题为单位代价，且问题有解时，一定能找到最优解
• BFS is a general problem-independent approach
  BFS是一个通用的与问题无关的方法.
• Low efficiency（效率较低）

（3）Depth-first Search 深度优先搜索 —DFS

• DFS is also derived from a general graph search algorithm.
  DFS也是从一般图搜索算法变化来的.
• DFS is to sort the nodes in Table OPEN in descending order according to the node depth in the search tree. The nodes with the biggest depth are arranged at the front of Table OPEN, and the nodes with the same depth can be
  arranged in any arrangement. Such a method is called “Depth-first search”.
  DFS就是把OPEN表中的结点按搜索树中结点深度的降序排序，深度最大的结点排在最前面，深度相同的结点可以任意排列。这样的搜索方式称为“深度优先搜索”。
• DFS always expands the deepest unexpanded node first.
  DFS总是首先扩展最深的未扩展节点。
  BFS always expands the shallowest unexpanded node first.
  BFS总是首先扩展最浅的未扩展节点。

Search Strategy 搜索策略

• DFS always expands the deepest node in the current Table OPEN of the
  search tree.
• The search proceeds immediately to the deepest level of the search tree, where the nodes have no successors.
• After those nodes are expanded, they are dropped from Table OPEN.
• so then the search “backs up” to the next deepest node that still has unexplored successors.
  DFS总是扩展搜索树的当前OPEN表中最深的结点。搜索很快推进到搜索树的最深层，那里的结点没有后继。当那些结点被扩展完之后，就从表OPEN中去掉，然后搜索算法回溯到下一个还有未扩展后继的深度稍浅的结点。

Implementation of DFS (DFS 的实现方法)

• Use LIFO (Last-In First-Out) stack to store Table OPEN, put successors at the top of the stack.使用 LIFO 栈存储OPEN表，把后继节点放在栈顶。
• Note: breadth-first-search uses a FIFO queue
  注意：宽度优先搜索使用 FIFO 队列。

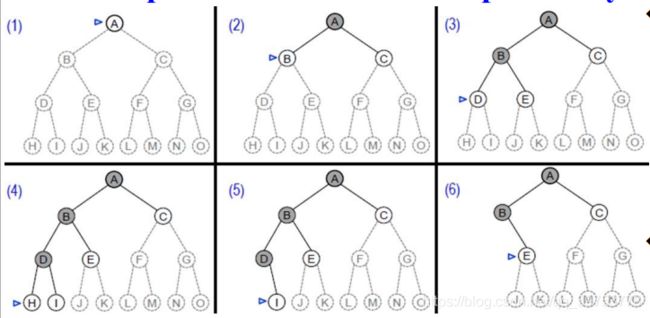
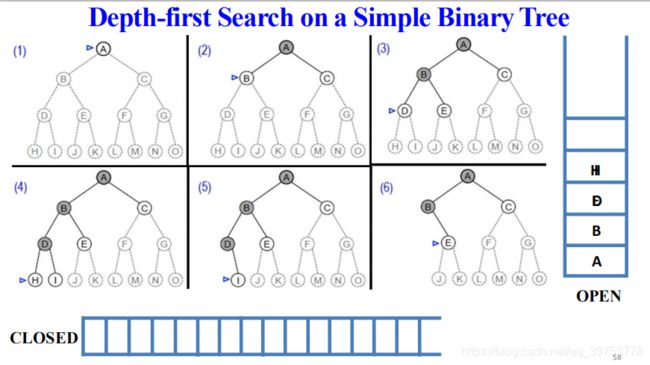
Depth-first Search on a Simple Binary Tree

• After a node is expanded, it is removed from the top of the stack (OPEN).
  一个结点被扩展后，就从OPEN表（栈）中将其删除。
  The expanded order (out of stack) is {H, I, D, J, K, E, B, L, M, F, N, O,G, C, A}.
• The black circles denote the explored and unexpanded nodes，which is pushed into the stack（OPEN）. 涂黑的圆圈表示已被探索过但未被扩展过的结点,随后被压入栈中；
• The circle pointed by a triangle denote the node to be explored next.
  三角指向的圆圈表示下一个将要被探索的结点。
  

Depth-first Search Algorithm

有界深度优先搜索算法

1. G:=G0(G0=s), OPEN:=(s), CLOSED:=( );
2. LOOP: IF OPEN=( ) THEN EXIT (FAIL);
3. n:=FIRST(OPEN);
4. IF GOAL(n) THEN EXIT (SUCCESS);
5. REMOVE(n, OPEN), ADD(n, CLOSED);
6. IF DEPTH(n)≥Dm GO LOOP;

// Dm is a threshold. 控制深度，以免陷入“深渊”

7. EXPAND(n) →{mi}, G:=ADD(mi, G);

// The set {mi} is established to include the successor nodes of n, but not the
ancestors of n, and these successor nodes are added to G.
// 扩展结点n，建立集合{mi}, 使其包含n的后继结点，而不包含n的祖先，并将这些后继结点加入G中。

8. IF Goal state is in{mi}, THEN EXIT(SUCCESS);

//IF 目标在{mi}中，则成功退出;

9. ADD(mj,OPEN), and mark the pointer from mj to n;

// mj denotes the nodes that are neither in Table CLOSED nor in Table OPEN.
ADD is to place mj in the tail of Table OPEN, so that the deepest nodes can be
extended preferentially.
// mj表示不在CLOSED和OPEN中的结点，ADD用于把mj放进OPEN表
后端，使深度最大的结点可优先扩展。

10. GO LOOP;
    
    
    The expanded order (out of stack) is {H, I, D, J, K, E, B, L, M, F, N, O,G, C, A}.

Features of DFS 深度优先搜索的性质

• There is no guarantee that the optimal solution can be found.
  一般不能保证找到最优解
• When the depth limit is not reasonable, the solution may not be found.
  当深度限制不合理时，可能找不到解.
• In the worst-case situation, search space is equivalent to exhaustion
  最坏情况时，搜索空间等同于穷举
• Compared with BFS, the advantage of DFS is that space complexity is low, because only one path from root to leaf is stored.
  与BFS相比，其优势在于：空间复杂度低，因为只存储一条从根到叶子的路径。
• DFS is a general problem-independent approach
  DFS是一个通用的与问题无关的方法.

（3）等代价搜索

等代价搜索=宽度优先搜索+ 最小代价

3.4 Informed Search Strategy (启发式搜索 Heuristic Search ）

The strategies use problem-specific knowledge beyond the definition of the problem itself, so that can find solutions more efficiently than can an uninformed strategy.
这类策略采用超出问题本身定义的、问题特有的知识，因此能够找到比无信息搜索更有效的解。
The general approaches use one or both of following functions:
一般方法使用如下函数中的一个或两者：

• An evaluation function, denoted f(n), used to select a node for expansion.
  评价函数，记作 f(n)，用于选择一个节点进行扩展。
• A heuristic function, denoted h(n), as a component of f.
  启发式函数，记作 h(n)，作为 f 的一个组成部分。

3.4.1 Best-First Search 最佳优先搜索

• Best-first search is an instance of the general GRAPH-SEARCH algorithm.
  最佳优先搜索是一般图搜索算法的一个实例。
• Best-first search is to sort all the nodes in Table OPEN according to the heuristic information, and the best node is ranked first, so it is called the “best first search”.
  最佳优先搜索就是把OPEN表中所有结点按照启发式信息排序，最佳结点排在最前面，因此称为“最佳优先搜索”

Search Strategy 搜索策略

• A node is selected for expansion based on an evaluation function, f(n).
  搜索策略：根据评价函数 f(n) 选择将要被扩展的节点。
• The evaluation function is construed as a cost estimate, so the node with the lowest evaluation is expanded first.
  评估函数被看作是代价估计，因此评估值最低的结点被选择首先进行扩展。

Heuristic Function (启发式函数)

Most best-first algorithms also include a heuristic function, h(n) as a component of f . 大多数的最佳优先算法的 f 中包含一个启发式函数h(n)。
h(n) = estimated cost of the cheapest path from the state at node n to a goal state.
h(n)=结点n 到目标结点的最小代价路径的代价估计值

Evaluation Function ：f(n)=h(n)+g(n).

Note: g(n) denotes the cost of the path from the initial state to Node n.
h(n) = estimated cost of the cheapest path from the state at node n to a goal state.

• If f(n) = g(n), it is called Uniform-cost Search. (一致代价搜索)
• If f(n) = g(n) = d(n), it is BFS. d(n)=搜索树的深度
  -If f(n) = h(n), it is called Greedy Best-First Search . (贪婪最佳优先搜索：不完备，搜索代价最小)

Implementation 实现方法

• Use FIFO queue to store Table OPEN.
• However best-first search uses f(n) instead of g(n) to order the priority queue.
  然而，最佳优先搜索使用f(n)，而不是用g(n)来对优先级队列进行排序。
• Identical to that for uniform-cost search.
  实现方法：与一致代价搜索相同
• Special cases 特例
  Greedy Search贪娈搜索 & A* search A* 搜索

3.4.2 A search （A 搜索）

• It is hoped that heuristic knowledge can be introduced to narrow the search scope and improve the search efficiency under the condition of finding the best solution. 希望引入启发知识，在保证找到最佳解的情况下，尽可能减少搜索范围，提高搜索效率。
• A search is a typical heuristic Graph search algorithm. A搜索是一种典型的启发式图搜索算法。
• Basic idea: define an evaluation function f, evaluate the current search status, and find out the most promising node to expand.
  基本思想：定义一个评价函数 f，对当前的搜索状态进行评估，找出一个最有希望的结点来扩展。

Search Strategy 搜索策略

• avoid expanding expensive paths, minimizing the total estimated solution cost.
  避免扩展代价高的路径，使总的估计求解代价最小化。
• Every time the elements in Table OPEN are sorted in ascending order according to f value.
  每次按照f 值的大小对OPEN表中的元素进行递增排序。
• Always select the node with the smallest f value of the current evaluation function to give priority to the expansion.
  每次扩展结点时，总是选择当前评价函数f值最小的结点来优先扩展。

Implementation 实现方法

Use FIFO (First-In First-Out) queue to store Table OPEN.

Evaluation Function ：f(n) = g(n) + h(n)

• g(n) ：the cost of the path from the initial state to Node n. (already happened)
• Heuristic Function h(n)： estimated cost of the cheapest path from n to the goal.
• f(n) = estimated cost of the cheapest solution through n .
• g*(n)： The cost of the shortest path from the initial state s to Node n.
  从 s（初始状态/结点）到结点 n 的最短路径的代价值. 可以准确计算
• h*(n)：The cost of the shortest path from Node n to the goal node.
  从结点n 到目标结点的最短路径的代价值.
• f*(n)=g*(n)+h*(n)：从s经过n到目标结点的最短路径的代价值.
  The cost of the shortest path from s to the goal node through n.

Symbol Representation

• g(n)、h(n)、f(n) is the estimate of g*(n), h*(n), f*(n), respectively.It is a kind of prediction.
  g(n)、h(n)、f(n)分别是g*(n)、h*(n)、f*(n)的估计值，是一种预测。
• g*(n) is the cost spent from the initial node s to Node n. The cost on the minimum-cost path from s to n, g(n),is calculated as the estimated value of g*(n).
  g*(n)是从初始结点s到达结点n 已花费的代价，计算从 s 到 n 的最小代价路径上的代价，作为g*(n)的估计值 g(n)。
• h*(n) is the cost from Node n to the goal node, which cannot be accurately calculated and can only be predicted. The prediction estimate h(n) can be referred to as heuristic information, depending on the knowledge in the field of problem.
• h*(n)是从结点n 到目标结点将要花费的代价，无法精确计算出来，只能预测.预测估计值h(n)可依靠问题领域的知识，称为启发式信息。

A search Algorithm

1. OPEN:=(s), f(s):=g(s)+h(s);

// s is the initial state/node.

2. LOOP: IF OPEN=( ) THEN EXIT(FAIL);
3. n:=FIRST(OPEN);
4. IF GOAL(n) THEN EXIT(SUCCESS);
5. REMOVE(n, OPEN), ADD(n, CLOSED);
6. EXPAND(n) →{mi}, compute f (n, mi):=g(n, mi)+h(mi);

//扩展结点n，建立集合{mi}，使其包含n的所有后继结点mi ，并计算每个mi的 f 值；
// mi is a successor of Node n. g(n, mi) is the cost from s to mi through n, f (n, mi) is the estimate of the cost from s and mi to the goal node through n;
// g(n, mi) 是从s经过n到达mi 的代价，
// f(n, mi)是从s经过n和mi 到达目标结点的代价的估计，是扩展 n 后的代价估计；
// h(mi) is the cost of the shortest path from mi to the goal node.h(mi)是从mi 到目标结点的最短路径的代价值.

ADD(mj, OPEN), and mark the pointer from mj to n;

// 标记mj 到n的指针；
// 将n 的后继中既不在OPEN中又不在CLOSED中的结点mj放入OPEN表中，并令mj 的指针指向n；
// mj is neither in OPEN，nor in CLOSED；mk is in Table OPEN, m1 is in Table CLOSED

(1) IF f(n, mk) THEN
f(mk):=f(n, mk), and mark the pointer from mk to n;

// f(mk) is the cost calculated before expanding n. If the condition holds, it means that the cost of the path from mk to the goal node after expanding n is lower than that before expanding n. The cost should be modified lower, and the pointer of mk should be modified to point to n.
// f(mk)是扩展 n 之前计算的代价，若条件1成立，说明扩展 n之后，从mk到目标结点的代价比扩展 n 之前的代价小，应修改mk的代价，并使mk的指针指向n。

(2) IF f(n, m1) THEN
{f(m1):=f(n, m1),；mark the pointer from ml to n; ADD(m1, OPEN); }

// 若条件2成立，则修改m1 的代价，且修改m1 的指针，使之指向n。
// 把m1 重新放回OPEN队列中，不必考虑改m1 后继结点的指针。

7. The nodes in Table OPEN are sorted in ascending order according to f value；

// OPEN中的结点按 f 值从小到大排序；

8. GO LOOP；

Note: if h=0, f(n)=d(n) (the depth of Node n), then A Search will degenerate into Breadth-First Search
若h=0，取估价函数f(n)=d(n)（结点n的深度），则A搜索将退化为广度优先搜索。

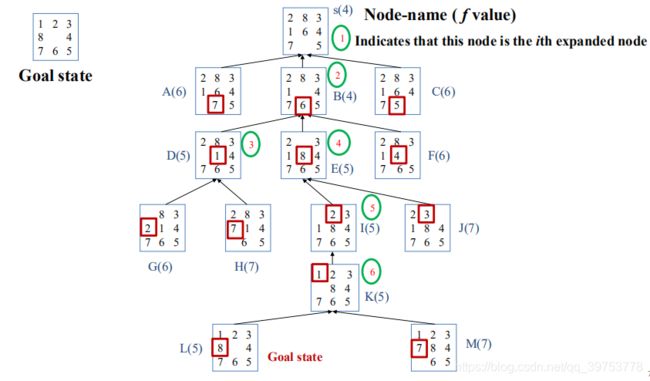
Solve 8-Puzzle problem using A Search Algorithm

Define the Evaluation Function ：f(n) = g(n) + h(n)

• g(n) is defined as the number of steps to move tiles, that is, the depth of Node n.
  g(n)为从初始状态到当前状态的代价值，定义为移动将牌的步数，即结点的深度.
• h(n) is defined as the number of misplaced tiles in the current state.
  h(n)是从n 到目标结点的最短路径的代价值，定义为当前状态中“不在位”的将牌数。
  

3.4.3 A* Search Algorithm （A*搜索算法）

• A Search Algorithm does not have any restrictions on the evaluation function f (n).
  A搜索算法没有对估价函数 f (n)做任何限制。
• In fact, the evaluation function is very important to the search process. If the selection is not proper, the solution of the problem may not be found, or the optimal solution of the problem may not be found.
  实际上，估价函数对搜索过程是十分重要的，如果选择不当，则有可能找不到问题的解，或者找到的不是问题的最优解。
• A* Algorithm is a heuristic search algorithm with some restrictions on the evaluation function.
  A* 算法就是对估价函数加上一些限制后得到的一种启发式搜索算法。
• In A algorithm, if the following condition is satisfied,
  h(n) ≤ h(n)*
  A algorithm is called A* algorithm.
  在A算法中，如果满足上述条件，则A算法称为A*算法。
• A∗ search is the most widely known form of best-first earch.
  A*搜索是最佳优先搜索的最广为人知的形式。
• A * algorithm is also known as the best graph search algorithm.
  A*算法也称为最佳图搜索算法。
• It is proved that if the problem has a solution, the solution can be found and the optimal solution can be found by using A* algorithm. Therefore, A * algorithm is better than A algorithm.
  可证明：若问题有解，则利用A* 算法一定能搜索到解，并且一定能搜索到最优解。因此，A* 算法比A算法好。

Example of A* condition

8-Puzzle problem

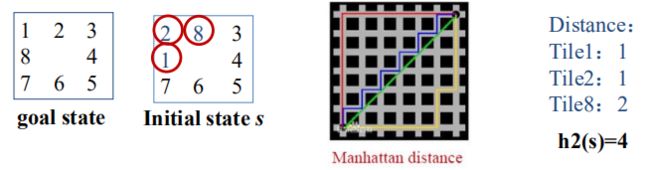
• To find shortest solutions by using A* , need a heuristic function that are two commonly used candidates.
  要用A*算法找到最短距离的解，需要一个启发式函数，通常有两个候选.
• h1(n) is defined as the number of misplaced tiles in the current state
  h1(n) = “不在位”的将牌数
• h2(n) is defined as the total Manhattan distance (tiles from desired locations)
  h2(n) = 所有将牌与其目标位置之间的距离之和。
  
• Let d(n) =The number of steps that have been moved, that is, the depth of Node n in the search tree
  已移动将牌的步数，即结点n在搜索树中的深度
• w(n)=the number of misplaced tiles in the state denoted by Node n
  结点n所表示的状态中“不在位”的将牌数
• To place w(n) " misplaced tiles " on their respective target positions, at least need to move w(n) steps. 将w(n)个“不在位”的将牌放在其各自的目标位置上，至少需要移动w(n)步。
• h(n)* is the actual number of steps from the current position of Node n to its target position, so obviously w(n) will not be greater than h*(n).
  h*(n)是从结点n从当前位置移动到目标结点的实际步数，显然 w(n) ≤ h*(n).
• Using w(n) as a heuristic function h(n) can satisfy the requirement of lower bound of h(n).
  以w(n)作为启发式函数h(n)，可以满足对h(n) 的下界的要求，即有 h(n)= w(n) ≤ h*(n).
• Therefore, when w(n) is chosen as a heuristic function to solve the 8-digit problem, A algorithm is also A* algorithm.
  因此，当选择w(n)作为启发式函数解决8数码问题时，A算法就是A*算法。
  
  h(n) is defined as the total Manhattan distance (tiles from desired locations)