Knowledge & Reasoning 复习
算法
自动图算法
Uninformed Search Strategies
- Breadth-First Search (BFS)
- Depth-First Search (DFS)
Sometimes better than BFS: Uniform-Cost Search
Safer DFS: Depth-Limited Search
Best of both: Iterative-Deepening Search
Breadth-First search (BFS) 广度优先搜索 02a
python-BFS-graph
python-BFS-tree
GfG的教学

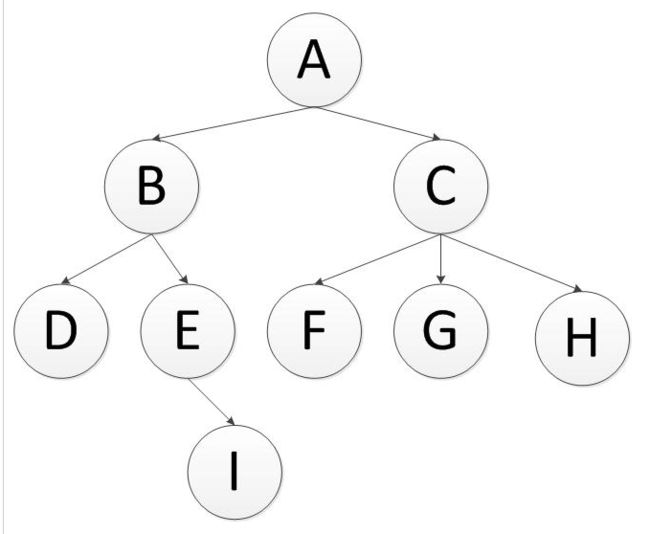
A,B,C,D,E,F,G,H,I(假设每层节点从左到右访问)。
First-in First-out!
(FIFO) Queue
Depth-First search (DFS) 深度优先搜索 02a
python -DFS-graph
python-DFS-tree
GfG的教学
A,B,D,E,I,C,F,G,H.(假设先走子节点的的左侧)
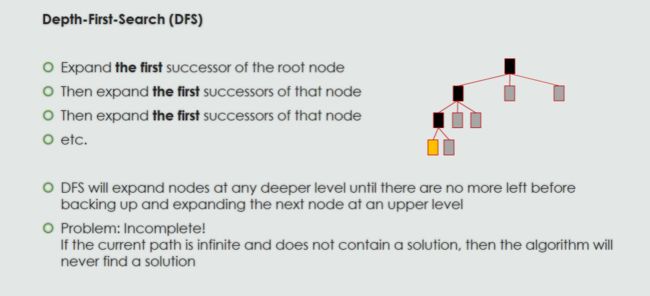
Last-In First-Out
Stack (LIFO Queue)
Depth-Limited Search (DLS) 深度限制搜索 02b
DLS 是一种折衷方案,提供了广度优先搜索的一些好处,同时减少了内存成本
从level 0 开始计数。
Iterative Deepening Search (IDS) 迭代深化搜索 02b
基于深度优先搜索
Iterative Deepening Depth First Search(IDDFS)
Uniform-Cost Search (UCS) 统一成本搜索 02b

思路:始终扩展最浅的路径,即具有最低(总体)路径成本的后继
python-ucs-graph
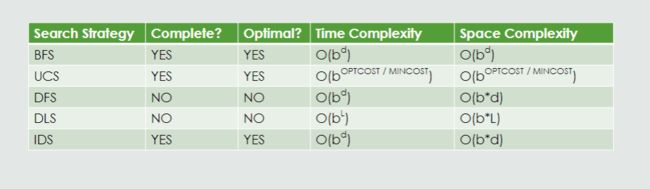
比较 03a
Difference between Informed and Uninformed Search
杂
How to formalise a problem for search
- Determine the relevant problem-solving knowledge
- Find a suitable state representation
- Define the initial state and the goal state(s)
- Define a transition model (also called successor function, or operators)
How to search
- Starting from the initial state, apply the successor function to reveal successor states
- Generate a search tree by expanding these states, and discovering their respective
successors, etc. - Perform a goal test for every node expanded
- Keep track of nodes waiting to get expanded (open list), and nodes already
expanded along the current path (the prospective solution).
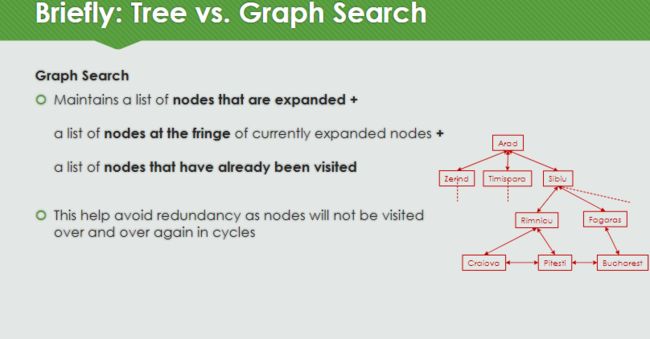
In graph search, we also keep a separate record of nodes already visited.
heuristic 03b
如何为问题提出启发式方法?
- Abstract from solution details
- Find a common property that can be quantified (not necessarily exact)
- Relax constraints (e.g., time needed, or accuracy of a solution)
- Keep the goal(s) in mind
- Not too complex – a heuristic should be cheap to compute and add little overhead
特质:
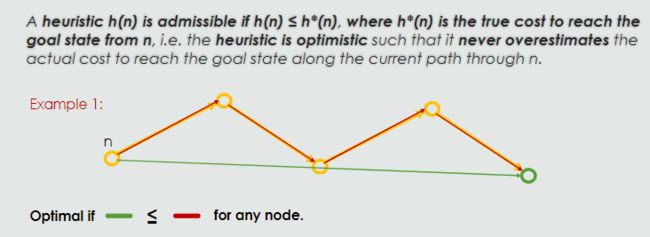
- Admissibility
它不会高估沿当前路径通过 n 到达目标状态的实际成本。
it does not overestimate the true path cost from any given node.
An admissible heuristic will ensure optimality when we use tree search.
The heuristic given here is admissible because it does not overestimate the true path cost from any given node.
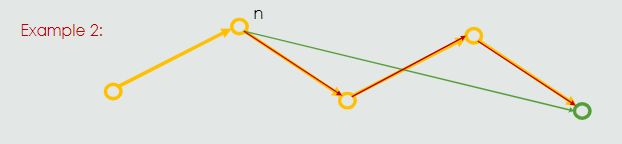
- Consistency
从 n 达到目标的估计成本不大于步骤成本 n
图搜索的时候不一致
A consistent heuristic will ensure optimality when we use graph search.
The heuristic given here is admissible because it does not overestimate the true path cost from any given node.
However, it is not consistent, because the heuristic overestimates at node B, because the step cost from B to C plus the estimated cost from C to the goal is less than the estimate from B.
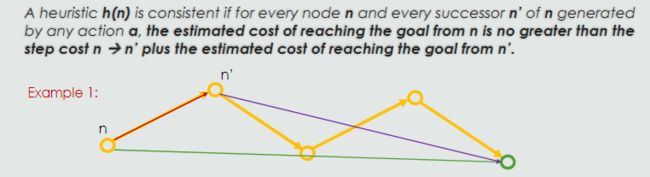
启发式算法例子:
Greedy Best-First Search
In greedy best-first search, the evaluation function contains a simple heuristic f(n) = h(n) that estimates the cost of the
cheapest path from the state at the current node to the node that has the goal state (straight-line distance).
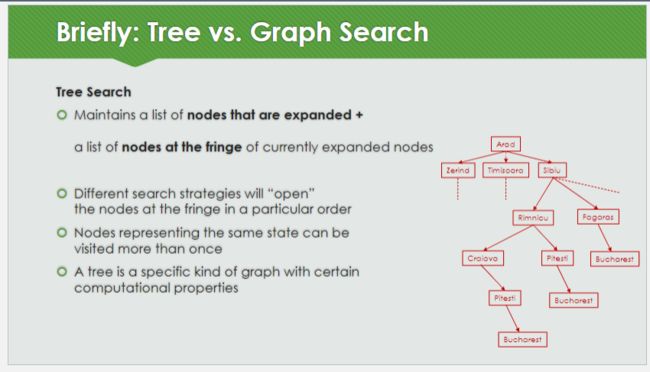
Tree vs. Graph Search 03b
A*启发式算法 04a
不断寻找最小点
use an evaluation function f(n) = g(n) + h(n)
简书教程
Lowest Evaluation Result First: g(n) + h(n)
Corresponding ADT: Priority Queue优先队列
Complete for finite spaces & positive path cost
Optimal: will always expand the currently best path
Optimally efficient (There is no other search algorithm that is guaranteed to expand fewer nodes and still find an optimal solution)
Space and time complexity depend on the heuristic chosen but can still be high in worst case, similar to BFS: bd
minimax 05ab
Adversarial Search
基于博弈论
- MAX: The player who starts (plays to win, pursues the path of highest utility)
- MIN: Player who follows (plays to minimise the other player’s result)
类似于DFS
High utility function results serve MAX, low values are good for MIN
添加链接描述
这个比较易懂
alpha beta 06ab
基于minimax加了alpha和beta
解和minimax一样
添加链接描述
添加链接描述
真的很抽象的一些理论知识
Epistemology 知识 07a
知识是什么:
- Explicit knowledge
that which is expressed in language - Implicit knowledge
that which can be expressed in language but is often not - Tacit knowledge
that which cannot be expressed in language because it is personal / embodied
知识从何而来:
经验主义:Acquired by learning from sensory stimulation: Empiricism(Connectionist AI)
理论主义: Acquired by reasoning: Rationalism(classic AI)
Deduction 07a
A premise in relation to a well-defined domain, class, or condition.
A premise about a concrete instance, hypothesis, or condition.
A conclusion based on the premises, i.e. the instance belonging to the domain, inheriting the characteristics defined for the class, or satisfying the condition.
向前推理和向后推理 07a
Forward reasoning:
Search connects initial fact(s) with desired conclusion(s).
States are combinations of facts and each rule is a method for generating a single successor (i.e., it defines a single transition).
Backward reasoning:
Search connects a final conclusion with one or more initial facts.
States are combinations of required conclusions and the transitions are defined by the rules. Each rule is a method for generating further `required conclusions’ from existing required conclusions.
What are the states?
→Forward reasoning: Facts
→Backward reasoning: Goal facts (Antecedents of conditions)
How does the successor function work?
→Forward reasoning: Application of rules to yield more facts
→Backward reasoning: Application of rules to yield more sub-goals
通常来说,搜索树在向前推理中是OR树,因为each node in a search tree branches according to the alternative transitions for a given state 。但是,in backwards reasoning, each node branches in two different ways because
we are usually compounding sub-goals that all need to be fulfilled for a solution.The branches from any node in a backward reasoning tree divide up into groups of logical AND branches, and each group presents an alternative chain (OR sub-tree).因此,反向推理中的搜索树是一个 AND/OR 树。
- Forward Reasoning 应用
Computational scientific discovery(e.g., chemical synthesis, simulating scientific discoveries from the past) - Backward Reasoning 应用
Repair assistance systems, Medical diagnosis support, Disaster recovery systems
Knowledge-based Systems / Expert Systems 07b
The combination of rule base and inference method can be viewed as a representation of knowledge for the domain, called a knowledge base.
A system which employs knowledge represented in this way is called a knowledge-based system or expert system.
An ideal knowledge representation
- Is expressive and concise
- Is unambiguous and context-independent
- Supports the creation of new knowledge from that which already exists
Propositional Logic 命题逻辑 07b
Formal methods of knowledge representation are also known as logics.
A formal logic is a system (often: symbols, grammar) for representing and analyzing statements in a precise, unambiguous way.
A logic usually has
- Sentences in a language, are expressions constructed according to formal rules.
- A semantics that identifies the formal meaning of the sentences.
- An inference method allows new sentences to be generated from existing sentences.
Propositions: P, Q, R, S, etc.
Connectives: AND ( ∧), OR ( ∨), NOT ( ¬ ), IMPLIES ( ⇒)
Constants: True ( T ), False ( F )
Others: parentheses for grouping expressions together
真值表:


Semantics:
This is called a referential semantics. The way one fact follows another should be mirrored by the way one sentence is entailed by another.
Predicate calculus / First-Order Logic (FOL) 谓词逻辑 07b
Move from simple propositions to predicates
Representation of properties, e.g., mortal(person)
Representation of relationships, e.g., likes(fred, sausages)
Existentially quantified variables, e.g., ∃x (There exists an x such that…)存在量化的变量
Universally quantified variables, e.g., ∀x (For all x we can say that…)普通量化的变量
∧ Conjunction (AND)
⇒ IMPLICATION
∀ Universal quantifier (“For all elements X…”)
∃ Existential quantifier (“Some X…”, “There is at least one X…”)


I wear a hat if it’s sunny:
sunny→ hat
I wear a hat only if it’s sunny:
hat → sunny
p only if q: p→ q
关于if和only if
other logics 07b
命题逻辑和谓词逻辑的区别
- Fuzzy logic: 模糊逻辑
Evaluation in terms of degree of set membership. - Modal logic: 模态逻辑
Evaluation in terms of a propositional attitude, such as belief.
Good for representing sentences containing “should”, “must”, etc. - Temporal logic: 时间逻辑
Evaluation in terms of truth at a particular moment in time. (“before”, “after”, etc.).
The Frame Problem 07b
句子表示的一个基本困难是框架问题。
这会影响所有种类的知识表示,但在根据真理进行评估并且使用规则来定义行为结果的情况下尤为明显。
在形式逻辑中,很难跟踪世界上事物的状态
Technical solutions:
指定影响和非影响
For a complete state representation, we would have to specify not only the effects of an action on the environment, but also the non-effects of that action (everything that does not change) in so-called frame axioms
但是这对于较大的框架是不可行的,所以框架问题的实际解决方案通常会尝试添加更通用的变量或谓词,以注意何时发生变化或可能发生变化
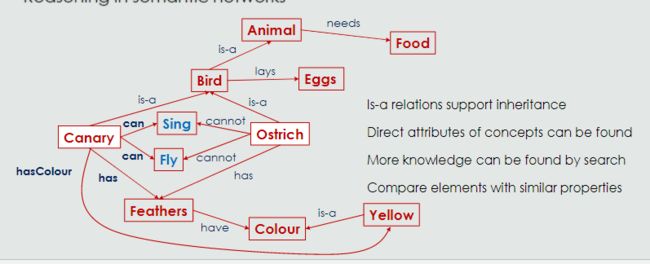
Semantic Networks语义网 08a
语义网络利用表示知识的有向图的结构
在语义网络中,节点代表概念,节点之间的联系表示概念之间的关系
非标准化语义网络缺乏统一的构建规则因此存在一致性和偏见问题
语义网络支持有限推理(例如,集合、继承、归纳)
传播激活搜索(如 BFS)效率低下,不受知识指导
frame 08a
Elements of a frame
- Unique identifier
- Relationships to other frames (e.g., conceptual inheritance)
- Requirements (Properties that must be true for this frame to apply to some thing)
- Procedural instructions (How we might use the thing described here, if applicable)
- Default properties of instances (established upon creation)
- Special properties of instances (elicited upon creation)
features:
- Allows easy and straightforward notation of abstraction in typical situations
- Descriptions can consider context: assumptions, expectations, or exceptions
- Instances can be distinguished from classes (instance_of, subclass_of)
- Less ambiguous than network diagrams as the structure is well-defined
- However, for the same reason, other relationships cannot be represented as easily
- Representation of time can be difficult
script 08a
Basics
- Effective representation of procedural knowledge in stereotypical situations
- Capture contextual knowledge for natural language understanding
- Enable a system to resolve ambiguity in language
- Very similar to frames, but time-ordered
- Transitions between script-frames supposed to resemble mental and physical
transitions in real life situations
Elements of a Script
- Entry conditions determine the activation of a script
- Results are facts that become true when a script has finished running
- Props are things that are needed to run the script – they illustrate the context to
which the script applies - Roles are the individual behaviours of the actors involved in a situation
- Scenes are used to decompose a script into different temporal episodes
Ontologies本体论 08b
formal categorisation and description of a body of knowledge
Ontology Components组件
- Classes (abstract or specific concepts)
- Individuals are Instances
- Properties of classes and individuals
- Relations between concepts
- Functions (computation of values)
- Axioms (logical restrictions)
Ontology Mapping映射
- Different domains or tasks usually have different ontologies (vocabulary, structure)
- Aligning ontologies allows communication between different systems
- Matching ontologies may even allow us to reason over one thing considering the vocabulary and structure of another (analogical reasoning)
- potentially awesome!
- New challenges: Matching ontologies not just within the same but in between different languages
Ontology Problems
- There is no single correct way of describing something! Consider different languages/cultures/concepts
- Languages are not static (new/old words & meanings)
- Hence, there is always a chance to have inconsistencies or limitations
- Not all knowledge can be represented as classes and relations; and some knowledge is extremely difficult to communicate:
- Knowledge Acquisition Bottleneck
- Finding the balance between clarity and extensibility is a challenge
How to specify Ontologies
- Conceptual data model: Resource Description Framework (RDF)
Set of W3C specifications
Based around resources (identifiable data / knowledge) - Any of the available languages, like
RDF-Schema (simple, extension of RDF vocabulary)
Web Ontology language (RDF-compatible, suited for reasoning)
and more…
Ontology Specification 规范
- Resource Description Framework (RDF)
A family of specifications, issued by the W3C consortium.
Triple-notation (Subject-Predicate-Object)主谓宾
Serialisable data (e.g., XML, JSON, etc.)
Data can be queried (SPARQL) - Web Ontology Language (OWL)
Family of specification languages for building ontologies (feed into RDF)
Stronger suited for reasoning
OWL comes in different flavours:
OWL Lite: Frame-based, supports related reasoning
OWL DL: Predicate-Logic-based, also known as Description Logics
OWL Full: Extension of RDF to support additional abstraction
Perspectives on Uncertainty对不确定性的看法 09a
不确定性对模糊/不精确知识 Related to vague or imprecise knowledge
不确定性和概率之间的联系:事件频率
Fuzzy Sets and Fuzzy Logic 模糊集和模糊逻辑 09a
- Fuzzy sets are non-probabilistic representations of uncertainty
- Fuzzy sets present an extension of classical set theory (classical sets are called crisp sets in Fuzzy set theory)
- Fuzzy logic describes operations over fuzzy sets
- Fuzzy logic is a superset of Boolean logic. Whereas the latter only knows True and False, in fuzzy logic everything is expressed to “a matter of degree”.
Membership functions specify the degree to which something belongs to a fuzzy set,它们代表可能性的分布而不是概率
建一个模糊关联矩阵
Applications
Antilock Braking system (ABS)
Washing machines (weight / intensity)
Expert Systems
Information Theory ,Bayesian 09b
不确定性可以用熵来衡量
不确定性是熵分布平坦度的函数
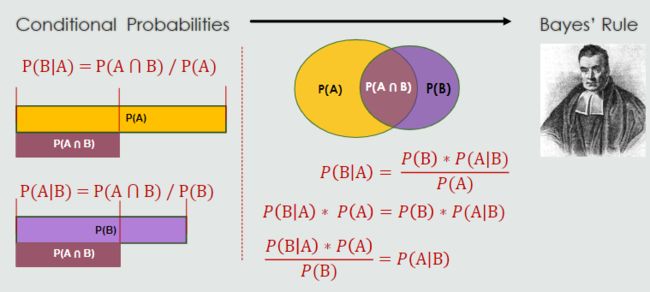
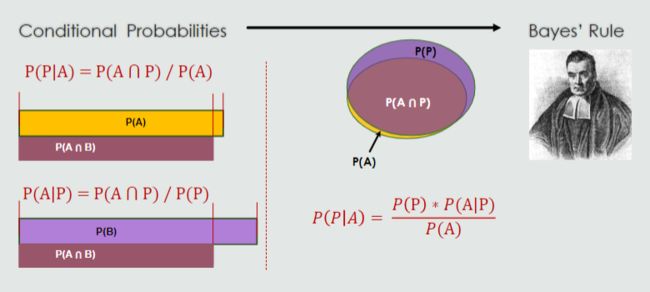
In Bayesian reasoning, probabilities can help establish an agent’s state of belief
(|) = ( ∗(|))/()
P© and P(E) are called prior probabilities.
P(E|C) is the likelihood.
P(C|E) is called the posterior probability
贝叶斯网络是一个Graphical Model,Directed graph, no cycles
Nodes: Variables (conditional probabilities)
Edges: Interactions between nodes (conditional interdependencies)
Probabilistic Modelling 10
Limitations of Bayesian Networks 贝叶斯网络的限制
- As in regular Bayesian reasoning, statistical data is required to populate your network, however there are also methods for simulation using random values
- Variables can only ever be influenced by their parents
- Cyclical influences are not directly supported
- If there are probability distributions in our chain that have high entropy, this “washes out” the conclusiveness of the overall result (especially if there are many of them)
Conditional entropy quantifies the uncertainty we have about some variable given we have observed another variable.
Bayes’ theorem allows calculating the conditional probabilities between variables
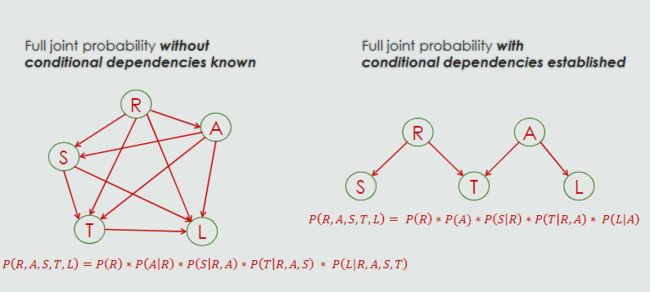
Bayesian networks explicitly encode the conditional dependencies between their variables
Bayesian networks implicitly encode the full joint probabilities of their variables also
Bayesian networks work great if there are strong correlations between probabilities.
Probability distributions with high entropy disturb the reasoning process as they have a tendency to reduce the clarity of results
Dynamic Bayesian Networks(DBN)11a
- A DBN is a generalisation of a Bayesian network (BN) that adds an additional dimension
- DBNs are used, for instance, to model temporal states of a domain or process
- A state of the domain is represented by multiple variables (not just one, as in BNs)
- State transitions describe how the domain is changing over time
DBNs are a class of knowledge representations for reasoning with conditional probabilities over an additional dimension (usually time)
DBNs often come in the form of discrete Markov processes, which involve a number of simplifying assumptions
Markov models are popular in Machine learning applications, such as speech and handwriting recognition, translation, or image processing but also others, such as the modelling of biological processes, or crypto-analysis
Markov Models 11a
A kind of DBN, also called a Markov Process
Describes the evolution of a system over time under uncertainty
There are different types of Markov models depending on the use of discrete or continuous v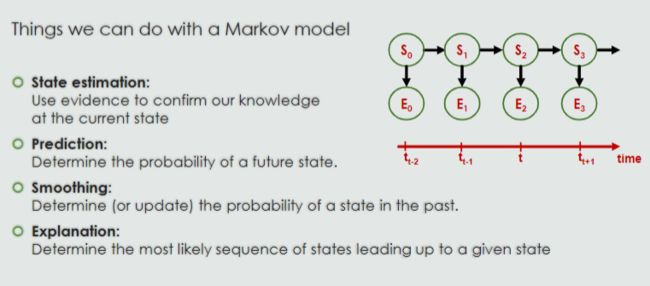
Markov Assumption马科夫假说:
A Markov model where the state of a system at any time t does depend solely on the previous state at t-1 is called a First-order Markov model
离散马尔可夫链:
逐步描述系统状态及其转换的模型
时间离散,状态描述也是如此
将状态转换的条件概率与矩阵运算来确定状态转换的概率。
模型可以保持相同状态或返回到以前的状态