k折交叉验证优缺点_【机器学习】训练集,验证集,测试集;验证和交叉验证...
在机器学习中,当我们把模型训练出来以后,该怎么对模型进行验证呢?(也就是说怎样知道训练出来的模型好不好?)有以下几种验证方式:
第一种方式:把数据集全部作为训练集,然后用训练集训练模型,用训练集验证模型(如果有多个模型需要进行选择,那么最后选出训练误差最小的那个模型作为最好的模型)
这种方式显然不可行,因此训练集数据已经在模型拟合时使用过了,再使用相同的数据对模型进行验证,其结果必然是过于乐观的。如果我们对多个模型进行评估和选择,那么我们可以发现,模型越复杂,其训练误差也就越小,当某个模型的训练误差看似很完美时,其实这个模型可能已经严重地过拟合了。(我们把这种由训练误差选出来模型称为gm-hat)
第二种方式:把数据集随机分为训练集和测试集,然后用训练集训练模型,用测试集验证模型(如果有多个模型需要进行选择,那么最后选出测试误差最小的那个模型作为最好的模型)
什么样的模型是好的?显然泛化误差最小的模型最好,但是我们没有这样的测试集能够测出模型的泛化误差。因此,我们把一部分数据作为测试集,用它的误差来模拟泛化误差。
把数据分出一部分作为测试集意味着训练集比原来小了。由学习曲线可知,使用较少的数据训练出来的模型,其测试误差会比较大。因此,对于多个模型的评估和选择,合理的做法是:用训练集训练出各个模型后,用测试集选出其中最好的模型(我们把此模型称为gm*-),记录最好模型的各项设置(比如说使用哪个算法,迭代次数是几次,学习速率是多少,特征转换的方式是什么,正则化方式是哪种,正则化系数是多少等等),然后用整个数据集再训练出一个新模型,作为最终的模型(我们把此模型称为gm*),这样得出的模型效果会更好,其测试误差会更接近于泛化误差。
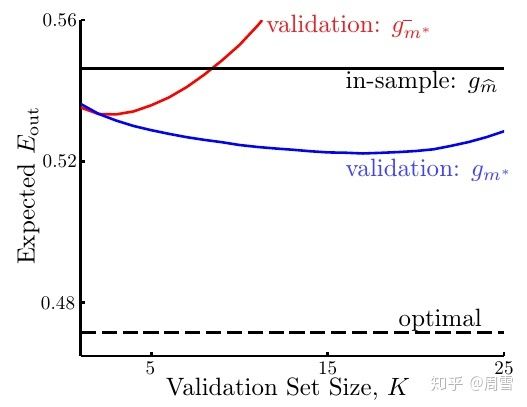
下图展示了随着测试集的增大,各个模型 -- gm*-(红线),gm*(蓝线),gm-hat(黑实线)的期望泛化误差和理想泛化误差(黑虚线)的变化趋势:
可以看到,gm*(蓝线)的表现最好,最接近于理想的泛化误差(黑虚线)。而随着测试集越来越大, gm*-(红线)的表现先是和gm*(蓝线)比较接近,然后越来越不如gm*(蓝线),最后甚至都不如gm-hat(黑实线)。这是因为测试集越大,用于训练的数据就越少,此时训练出的模型的效果肯定也就不好了。因此,在选择测试集的大小时,其实有个两难境地:如果要使gm*(蓝线)的期望泛化误差接近于理想泛化误差,就需要让测试集比较大才好,因为这样有足够多的数据模拟未知情况,但是这样一来,gm*(蓝线)和gm*-(红线)的期望泛化误差之间的差距就比较大;而要想让gm*(蓝线)和gm*-(红线)的期望泛化误差接近,就需要测试集比较小才好,因为这样有足够多的数据训练模型,但是此时gm*(蓝线)的期望泛化误差和理想泛化误差之间的差距较大。一般来说,人们通常将测试集的大小设置为所有数据的20%~30%。
很多资料都是这样把数据分为训练集(70%-80%)和测试集(20%-30%)。这样做的前提是:把模型各个可能的设置分别列出来,训练出各个不同的模型,然后用测试集选出最好的模型,接下来用全部数据按照最好模型的各项设置重新训练出一个最终的模型。这样做有两个问题。第一,模型的超参数通常很多,我们不太有可能把所有可能的设置全部罗列出来,超参数通常需要根据实际情况进行调整。如果模型的测试成绩不理想,那么我们需要返回,重新训练模型。虽然测试集不用于模型的训练,但是我们如果基于测试误差来不断调整模型,这样会把测试集的信息带入到模型中去。显然,这样是不可行的,因为测试集必须是我们从未见过的数据,否则得出的结果就会过于乐观,也就会导致过拟合的发生。第二,得出的最终的模型,其泛化误差是多少?我们还是无法评估。因为我们又把全部数据重新训练出了这个最终的模型,因此也就没有从未见过的数据来测试这个最终的模型了。
第三种方式:把数据集随机分为训练集,验证集和测试集,然后用训练集训练模型,用验证集验证模型,根据情况不断调整模型,选择出其中最好的模型,再用训练集和验证集数据训练出一个最终的模型,最后用测试集评估最终的模型
这其实已经是模型评估和模型选择的整套流程了。在第二种方式中,我们已经把数据集分为了训练集和测试集,现在我们需要再分出一个测试集,用于最终模型的评估。因为已经有一个测试集了,因此我们把其中一个用于模型选择的测试集改名叫验证集,以防止混淆。(有些资料上是先把数据集分为训练集和测试集,然后再把训练集分为训练集和验证集)
前几个步骤和第二种方式类似:首先用训练集训练出模型,然后用验证集验证模型(注意:这是一个中间过程,此时最好的模型还未选定),根据情况不断调整模型,选出其中最好的模型(验证误差用于指导我们选择哪个模型),记录最好的模型的各项设置,然后据此再用(训练集+验证集)数据训练出一个新模型,作为最终的模型,最后用测试集评估最终的模型。
由于验证集数据的信息会被带入到模型中去,因此,验证误差通常比测试误差要小。同时需要记住的是:测试误差是我们得到的最终结果,即便我们对测试得分不满意,也不应该再返回重新调整模型,因为这样会把测试集的信息带入到模型中去。
第四种方式:交叉验证(Cross Validation)简单来说就是重复使用数据。除去测试集,把剩余数据进行划分,组合成多组不同的训练集和验证集,某次在训练集中出现的样本下次可能成为验证集中的样本,这就是所谓的“交叉”。最后用各次验证误差的平均值作为模型最终的验证误差。
为什么要用交叉验证?大家知道,之前我们说的留出法(holdout)需要从数据集中抽出一部分作为验证集。如果验证集较大,那么训练集就会变得很小,如果数据集本身就不大的话,显然这样训练出来的模型就不好。如果验证集很小,那么此验证误差就不能很好地反映出泛化误差。此外,在不同的划分方式下,训练出的不同模型的验证误差波动也很大(方差大)。到底以哪次验证误差为准?谁都不知道。但是如果将这些不同划分方式下训练出来的模型的验证过程重复多次,得到的平均误差可能就是对泛化误差的一个很好的近似。
交叉验证的几种方法:
1. 留一法(Leave One Out Cross Validation,LOOCV)
假设数据集一共有m个样本,依次从数据集中选出1个样本作为验证集,其余m-1个样本作为训练集,这样进行m次单独的模型训练和验证,最后将m次验证结果取平均值,作为此模型的验证误差。
(注:这里说的数据集都是指已经把测试集划分出去的数据集,下同)
留一法的优点是结果近似无偏,这是因为几乎所有的样本都用于模型的拟合。缺点是计算量大。假如m=1000,那么就需要训练1000个模型,计算1000次验证误差。因此,当数据集很大时,计算量是巨大的,很耗费时间。除非数据特别少,一般在实际运用中我们不太用留一法。
2. K折交叉验证(K-Fold Cross Validation)
把数据集分成K份,每个子集互不相交且大小相同,依次从K份中选出1份作为验证集,其余K-1份作为训练集,这样进行K次单独的模型训练和验证,最后将K次验证结果取平均值,作为此模型的验证误差。当K=m时,就变为留一法。可见留一法是K折交叉验证的特例。
根据经验,K一般取10。(在各种真实数据集上进行实验发现,10折交叉验证在偏差和方差之间取得了最佳的平衡。)
3. 多次K折交叉验证(Repeated K-Fold Cross Validation)
每次用不同的划分方式划分数据集,每次划分完后的其他步骤和K折交叉验证一样。例如:10 次 10 折交叉验证,即每次进行10次模型训练和验证,这样一共做10次,也就是总共做100次模型训练和验证,最后将结果平均。这样做的目的是让结果更精确一些。(研究发现,重复K折交叉验证可以提高模型评估的精确度,同时保持较小的偏差。)
4. 蒙特卡洛交叉验证(Monte Carlo Cross Validation)
即将留出法(holdout)进行多次。每次将数据集随机划分为训练集和验证集,这样进行多次单独的模型训练和验证,最后将这些验证结果取平均值,作为此模型的验证误差。与单次验证(holdout)相比,这种方法可以更好地衡量模型的性能。与K折交叉验证相比,这种方法能够更好地控制模型训练和验证的次数,以及训练集和验证集的比例。缺点是有些观测值可能从未被选入验证子样本,而有些观测值可能不止一次被选中。(偏差大,方差小)
总结:在数据较少的情况下,使用K折交叉验证来对模型进行评估是一个不错的选择。如果数据特别少,那么可以考虑用留一法。当数据较多时,使用留出法则非常合适。如果我们需要更精确一些的结果,则可以使用蒙特卡洛交叉验证。
此外,需要特别注意的是:如果我们要对数据进行归一化处理或进行特征选择,应该在交叉验证的循环过程中执行这些操作,而不是在划分数据之前就将这些步骤应用到整个数据集。
上面说的是对单个模型进行的交叉验证。如果要在多个不同设置的模型中进行选择,那么步骤和验证类似:首先将数据集划分为训练集和测试集,然后用交叉验证方法划分训练集(划分为训练集和验证集),训练出不同模型后,按验证集误差选出其中最好的模型,记录最好模型的各项设置,然后据此再用(训练集+验证集)数据训练出一个新模型,作为最终的模型,最后用测试集评估最终的模型。
可以看出,在上述模型评估和模型选择过程中,除了对模型进行评估之外,验证和交叉验证还有另外一个作用,就是对超参数进行优化。之前我们所说的根据情况不断调整模型就是其中一种超参数优化方式,叫做试错。另外一种超参数优化方式是:列出各种不同超参数设置的算法;使用验证或交叉验证方法在训练数据上训练出这些不同的模型,然后对这些模型在验证集上的性能进行评估;之后选择其中最好的模型对应的超参数设置。这种超参数优化方式称为网格搜索,当然还有其他的超参数优化方式。
对于超参数优化,推荐用10折交叉验证。
第五种方式:自助法 --- 具体请见《自助法(Bootstraping)》
总结一下:
训练集(Training Set):用于训练模型。
验证集(Validation Set):用于调整和选择模型。
测试集(Test Set):用于评估最终的模型。
当我们拿到数据之后,一般来说,我们把数据分成这样的三份:训练集(60%),验证集(20%),测试集(20%)。用训练集训练出模型,然后用验证集验证模型,根据情况不断调整模型,选出其中最好的模型,记录最好的模型的各项选择,然后据此再用(训练集+验证集)数据训练出一个新模型,作为最终的模型,最后用测试集评估最终的模型。