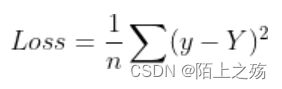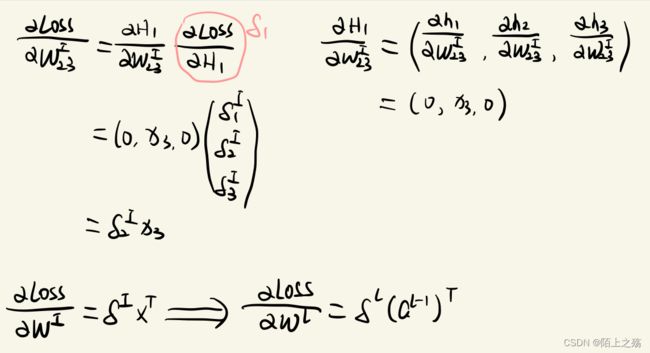numpy实现反向传播【超级小白讲解】

本文记录简易神经网络反向传播的推导过程，并用numpy搭建一个神经网络和实现反向传播的过程。
参考教材：邱锡鹏《神经网络与深度学习》4.4反向传播算法
本文也参考了另一位大神的文章：numpy搭建简易神经网络

一.神经网络数据

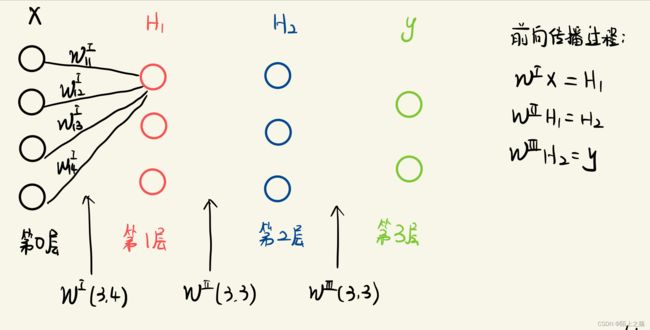
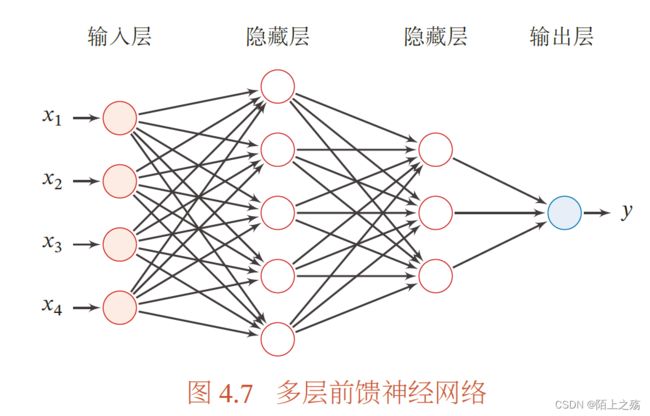
搭建了一个三层神经网络，包括两个隐藏层，一个输出层，输入4个节点，隐藏层都为3个节点，输出层2个节点。（在本例中忽略偏置b）
一些符号说明：
X ：为一个4维的列向量，即[x1,x2,x3,x4].T,但是在计算时要将他作为一个四行一列的二维矩阵去运算，X=(4,1)
Y ：真实值，二维的列向量，同理，运算时要变成一个二行一列的二维矩阵去运算，Y=(2，1)
L ：层数，层数一般只考虑隐藏层和输出层，输入层也可称为第0层。
W ：某一层的权重矩阵，下面右上角的罗马数字代表第几层
第L层的权重矩阵的shape应当是(ML,ML-1),ML代表该层的节点数。
搭建的神经网络如下图所示:（因为所有线画出来很繁杂，就只画了一小部分）

二.搭建神经网络

2.1 前向传播

神经网络的关系式（也可以说是前向传播 ）如下：（后面反向传播的时候，一定要根据这里的关系式求）

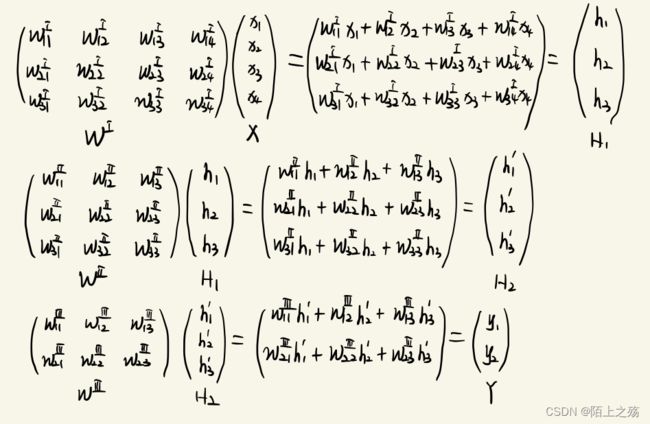注：本例前向传播的时候为了方便，设所有的激活函数都为f(x)=x，就等于他本身，求导为1

# 正向传播
 H1 = np.dot(w1, X)   # 第1个隐藏层
 H2 = np.dot(w2, H1)  # 第2个隐藏层
 y = np.dot(w3, H2)   # 输出层

2.2 误差

本例误差采用均方误差，Loss的值应当是一个标量，公式为：

loss = np.sum((Z-y)**2)/2

2.3 反向传播详细推导

先推导反向传播的一般式，再看本例。
假设损失函数为L，那么就需要计算损失函数关于每个参数的导数。但是计算$\frac{\partial Loss}{\partial W}$比较复杂，所以我们利用链式法则，分别求出对每一个具体的权重的偏导，最后再拼回矩阵。
先看一些符号定义（下图来自邱锡鹏《神经网络与深度学习》)

根据链式法则，对某个权值求导的公式为$\frac{\partial Loss}{\partial Wij}$=$\frac{\partial Z}{\partial Wij}$$\frac{\partial Loss}{\partial Z}$，定义误差项δ=$\frac{\partial Loss}{\partial Z}$，误差项其实目标函数关于第 层的神经元$Z^{(l)}$的偏导数。在计算上面式子之前，先看一看矩阵对矩阵求导的基本方法。（下图来自《矩阵论简明教程第3版》）

了解了矩阵对矩阵求导的基本定义后，现在来计算上面的式子，如下图：
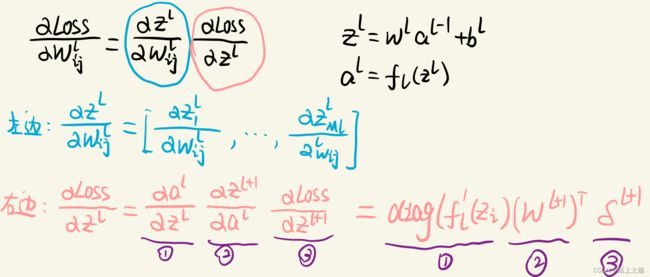对于左边，向量对标量求导，还是一个向量。
对于右边，分为三个部分，我们分别来看。具体过程如下图（写的很详细了哦）：

从上面的推断我们可以看出，第 层的误差项可以通过第 +1层的误差项计算得到，这就是误差的反向传播。反向传播算法的含义是：第 层的一个神经元的误差项是所有与该神经元相连的第 + 1 层的神经元的误差项的权重和，然后，再乘上该神经元激活函数的梯度。
所以我们的求解方式就是，从后往前计算每一层的误差项，再对每一层的权重求导。

2.4 本例反向传播

现在就根据上面的方式，求解本例的反向传播。首先计算最后一层的误差项$\delta 3$，如下图：
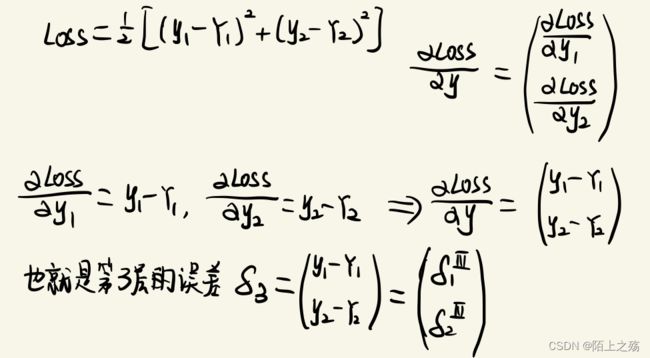再用反向传播依次求前两层的误差

# 求误差
s3 = y - Y
s2 = np.dot(w3.T, s3)
s1 = np.dot(w2.T, s2)

现在每一层的误差项已经求出来了，接下来就求对权重矩阵求导。先看对某一个权值的导数，然后得出对每一层权重矩阵的导数，如下图：

# 求偏导
dw1 = np.dot(s1, X.T)
dw2 = np.dot(s2, H1.T)
dw3 = np.dot(s3, H2.T)

# 更新w
w1 = w1 - lr * dw1
w2 = w2 - lr * dw2
w3 = w3 - lr * dw3

三. 完整numpy实现

import numpy as np
import matplotlib.pyplot as plt

train_loss = [] # 记录每一次的损失，为了可视化
def train(X, Y, lr, num_epochs):
    # 随机生成权重参数
    w1 = np.random.randn(3, 4)
    w2 = np.random.randn(3, 3)
    w3 = np.random.randn(2, 3)
    for epoch in range(num_epochs):
        # 正向传播
        H1 = np.dot(w1, X)   # 第1个隐藏层
        H2 = np.dot(w2, H1)  # 第2个隐藏层
        y = np.dot(w3, H2)   # 输出层
        loss = np.sum((Y - y) ** 2) / 2
        print(f'{epoch+1}轮的损失：{loss}')
        train_loss.append(loss)
        # 求误差
        s3 = y - Y
        s2 = np.dot(w3.T, s3)
        s1 = np.dot(w2.T, s2)
        # 求偏导
        dw1 = np.dot(s1, X.T)
        dw2 = np.dot(s2, H1.T)
        dw3 = np.dot(s3, H2.T)
        # 更新w
        w1 = w1 - lr * dw1
        w2 = w2 - lr * dw2
        w3 = w3 - lr * dw3
    return w1, w2, w3


# 创建数据
X = np.array([[1], [2], [3], [4]]) # 训练集
Y = np.array([[10], [20]]) # 真实数据
# 训练
w1, w2, w3 = train(X, Y, 0.001, 10)
print(w1)
print(w2)
print(w3)

# 预测，相当于前向传播
H1 = np.dot(w1, X)
H2 = np.dot(w2, H1)
y = np.dot(w3, H2)
print(f'预测数据为{y}')
# 可视化
plt.plot(range(1,11), train_loss)
plt.title('train loss')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

代码运行结果如下：

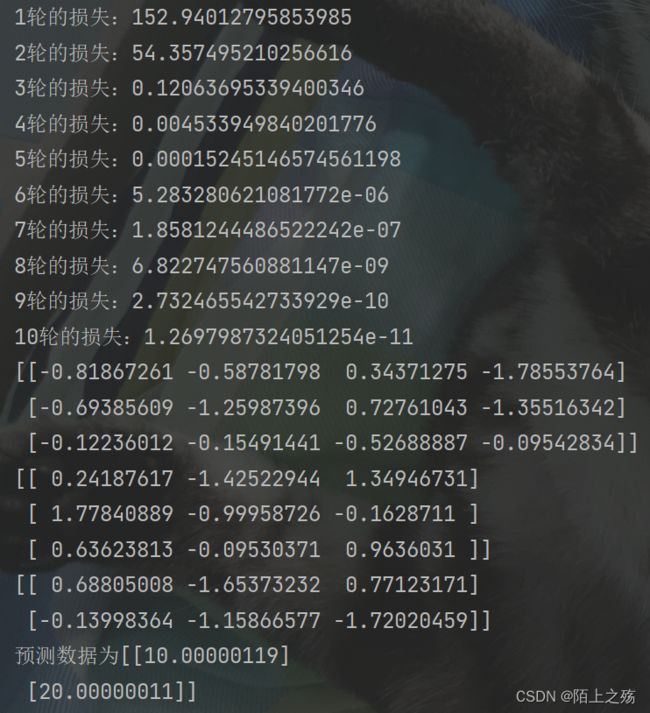
可视化结果如下：

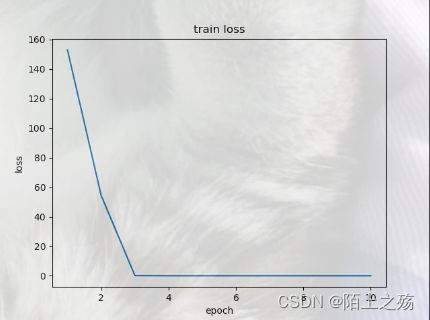
可以看到，最后的结果和真实数据非常接近，损失在第4轮训练就基本接近于0了。所以，拟合是非常成功的。

最后

本人也只是深度学习初学者，本文也是为了记录自己学习反向传播的过程，由于公式繁杂，所以大部分采用手写截图的方式，如果有误，请指正。