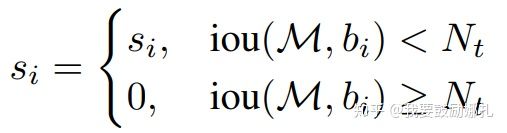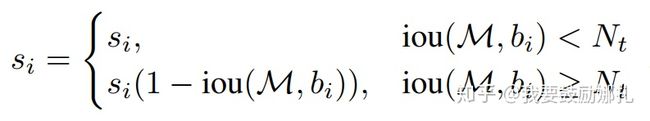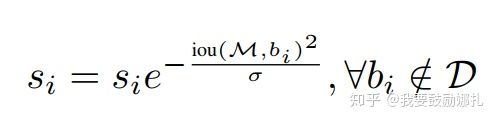什么是soft matting方法_NMS、 soft-nms、softer-nms

NMS检测框合并策略

一.NMS

1.NMS算法过程

NMS主要就是通过迭代的形式，不断的以最大得分的框去与其他框做IoU操作，并过滤那些IoU较大（即交集较大）的框。

①根据候选框的类别分类概率做排序，假如有4个 BBox ，其置信度A>B>C>D。

②先标记最大概率矩形框A是算法要保留的BBox；

③从最大概率矩形框A开始，分别判断ABC与D的重叠度IOU（两框的交并比）是否大于某个设定的阈值(0.5)，假设D与A的重叠度超过阈值，那么就舍弃D；

④从剩下的矩形框BC中，选择概率最大的B，标记为保留，然后判断C与B的重叠度，扔掉重叠度超过设定阈值的矩形框；

⑤一直重复进行，标记完所有要保留下来的矩形框。

two stage算法，通常在选出BBox有BBox位置(x,y,h,w)和是否是目标的概率，没有具体类别的概率。因为程序是生成BBox，再将选择的BBox的feature map做rescale (一般用ROI pooling)，然后再用分类器分类。NMS一般只能在CPU计算，这也是two stage相对耗时的原因。

但如果是one stage做法，BBox有位置信息(x,y,h,w)、confidence score，以及类别概率，相对于two stage少了后面的rescale和分类程序，所以计算量相对少。

2.NMS缺点

1、NMS算法中的最大问题就是它将相邻检测框的分数均强制归零(即将重叠部分大于重叠阈值Nt的检测框移除)。在这种情况下，如果一个真实物体在重叠区域出现，则将导致对该物体的检测失败并降低了算法的平均检测率。

2、NMS的阈值也不太容易确定，设置过小会出现误删，设置过高又容易增大误检。

3、NMS一般只能使用CPU计算，无法使用GPU计算。

3.假设这是一个函数，那么这个函数输入输出是什么，中间操作又是怎么做的

输入是各种bouding box的位置坐标信息B及其对应分数S，以及阈值threshold，操作流程可见下图。

二.soft-nms

1.算法流程

NMS算法是略显粗暴，因为NMS直接将删除所有IoU大于阈值的框。soft-NMS吸取了NMS的教训，在算法执行过程中不是简单的对IoU大于阈值的检测框删除，而是降低得分。算法流程同NMS相同，但是对原置信度得分使用函数运算，目标是降低置信度得分.

bi为待处理BBox框，B为待处理BBox框集合，si是bi框更新得分，Nt是NMS的阈值，D集合用来放最终的BBox，f是置信度得分的重置函数。 bi和M的IOU越大，bi的得分si就下降的越厉害。

经典的NMS算法将IOU大于阈值的窗口的得分全部置为0，可表述如下：

论文置信度重置函数有两种形式改进，一种是线性加权的：

一种是高斯加权形式：

具体代码实现：

可以明显看到soft-NMS最重要是更新weight变量的值。采用线性加权时，更新为1-ov,高斯加权时引入sigma参数，而原始NMS算法时，直接取0或1。

2.soft-nms优缺点分析

优点：

1、Soft-NMS可以很方便地引入到object detection算法中，不需要重新训练原有的模型、代码容易实现，不增加计算量（计算量相比整个object detection算法可忽略）。并且很容易集成到目前所有使用NMS的目标检测算法。

2、soft-NMS在训练中采用传统的NMS方法，仅在推断代码中实现soft-NMS。作者应该做过对比试验，在训练过程中采用soft-NMS没有显著提高。

3、NMS是Soft-NMS特殊形式，当得分重置函数采用二值化函数时，Soft-NMS和NMS是相同的。soft-NMS算法是一种更加通用的非最大抑制算法。

缺点：

soft-NMS也是一种贪心算法，并不能保证找到全局最优的检测框分数重置。除了以上这两种分数重置函数，我们也可以考虑开发其他包含更多参数的分数重置函数，比如Gompertz函数等。但是它们在完成分数重置的过程中增加了额外的参数。

三.softer-nms

1.softer-nms算法思想

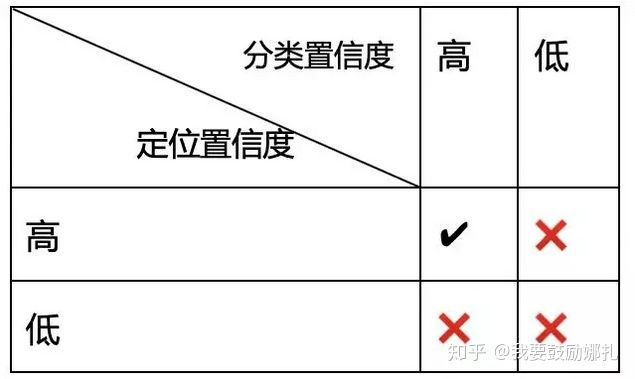
论文的motivation来自于NMS时用到的score仅仅是分类置信度得分，不能反映Bounding box的定位精准度，既分类置信度和定位置信非正相关的。NMS只能解决分类置信度和定位置信度都很高的，但是对其它三种类型：“分类置信度低-定位置信度低”，“分类置信度高-定位置信度低”，“分类置信度低-定位置信度高“都无法解决。

论文首先假设Bounding box的是高斯分布，ground truth bounding box是狄拉克delta分布（即标准方差为0的高斯分布极限）。KL 散度用来衡量两个概率分布的非对称性度量，KL散度越接近0代表两个概率分布越相似。

论文提出的KL loss，即为最小化Bounding box regression loss，既Bounding box的高斯分布和ground truth的狄拉克delta分布的KL散度。直观上解释，KL Loss使得Bounding box预测呈高斯分布，且与ground truth相近。而将包围框预测的标准差看作置信度。

论文提出的Softer-NMS，基于soft-NMS，对预测标注方差范围内的候选框加权平均，使得高定位置信度的bounding box具有较高的分类置信度。

2.网络结构

如所示Softer-NMS网络结构，与R-CNN不同的是引入absolute value layer（图中AbsVal）,实现标注方差的预测。

如上图 所示Softer-NMS的实现过程，其实很简单，预测的四个顶点坐标，分别对IoU＞Nt的预测加权平均计算，得到新的4个坐标点。第i个box的x1计算公式如下（j表示所有IoU＞Nt的box）：

考虑特殊情况，可以认为是预测坐标点之间求平均值。

3.代码

softerNMS的开源代码在https://github.com/yihui-he/softerNMS。

在softer-NMS/detectron/core/test.py有Softer-NMS(配置cfg.STD_NMS), Soft-NMS(配置cfg.TEST.SOFT_NMS.ENABLED)以及NMS的实现

在softer-NMS/detectron/utils/py_cpu_nms.py文件有Softer-NMS的具体实现，加权求平均在47-48行代码实现：

4.优缺点分析

1、个人认为论文提出的KL loss就是曼哈顿距离，但是通过KL散度去证明，让数学不太好的同学不明觉厉。

2、论文提出的Softer-NMS,本质是对预测的检测框加权求平均，为什么要这样，以及为什么让box高度重叠？个人认为Softer-NMS的理论没有在应该什么的地方深入。