基于插值的超分辨率图像重建算法（1）

       基于插值的方法通常提供过于平滑的重建图像，失去部分细节，留下了振铃效应（输出图像灰度剧烈变化处产生的震荡，尤其是高频信息丢失）。

       基于插值的重建方法通常有三类：1、最近邻插值法 2、双线性插值法 3、双三次插值法

1、最邻近插值法（Nearest neighbor）：令变换后像素灰度值等于离它最近的输入像素的灰度值。最邻近插值法的核心思想是找出距离输出像素点最近的点，则该点的像素值的灰度值就是输出点的像素值的灰度值。                              

        

    

 

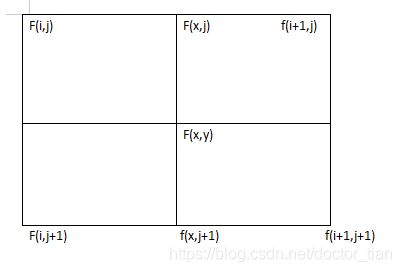
2.双线性插值法（Bilinear interpolation algorithm）:其中心思想是通过中心像素点旁边四个相邻点f(i,j),f(i+1,j),f(i,j+1),f(i+1,j+1)的像素分别在水平和垂直两个方向上做线性内插得到最终待插值点的像素值。

        模型：由插值公式:，其中（x,y）为待插入像素值,(x1,y1),(x2,y2)为已知值。

                             化简可得:f(x,j)=(i+1-x)f(i,j)+(x-i)f(i+1,j)

                                            f(x,j+1)=(i+1-x)f(i,j+1)+(x-i)f(i+1,j+1)

                                            f(x,y)=(j+1-y)f(x,j)+(y-j)f(x,j+1)

                                    得出:f(x,y)=(j+1-y)(j+1-x)f(i,j)+(j+1-y)(x-i)f(i+1,j)+(y-j)(i+1-x)f(i,j+1)+(y-j)(x-i)f(i+1,j+1)

双线性插值算法仅仅考虑到4个直接临近点的灰度的影响，考虑影响因素太小

 

 

3.双三次插值法（bicubic interpolation）：双三次插值将带采样点旁的4个邻点扩展为16个，对这16个邻点灰度值做三次插值。

  其模型为：

  双三次插值需要合适的插值基函数来拟合数据，常用插值基函数数学表达式如下: