Motion Planning for Mobile Robots:地图
地图主要分为两个部分:一个是用于装载数据、存储信息的数据结构,另一个是地图中信息融合的方法
Occupancy grid map 占用的栅格地图
最为常见、应用最为广泛、实现较简单
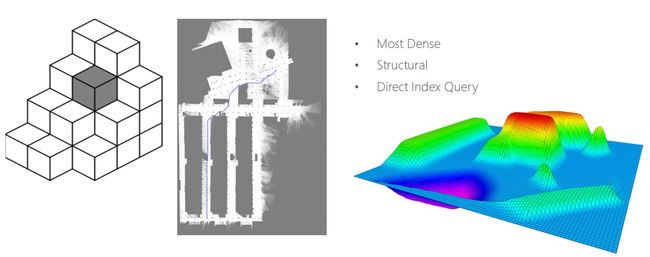
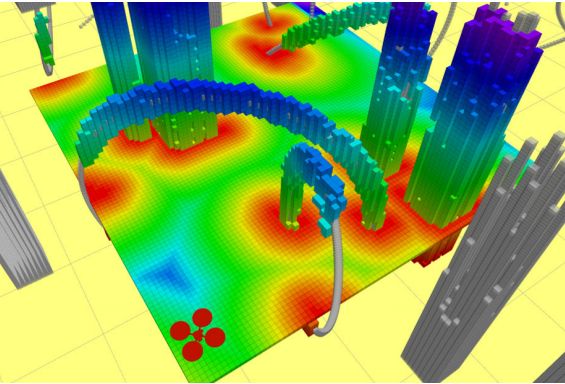
上图中我们可以看见多种形态的栅格地图,左一是一个3D的栅格地图、中间是2D的栅格地图、右一是2.5D的栅格地图。2.5D的地图也是在平面空间上进行划分,但区别在于每一个网格会有自己的高度,我们一般也称这种2.5D的地图为海拔地图。
Most Dense 最稠密的建图,要对xyz方向进行密集的切分
Structural 排列的非常紧密,具有结构化的特征
Direct Index Query 其最大的优势在于可以直接根据坐标索引进行查询,查询是O(1)的复杂度
当分辨率比较高,即在空间中切分比较密集时,栅格地图占用的内存将非常大。
https://github.com/ANYbotics/grid_map
Occupancy grid map的主要作用就是将有噪声的传感器给收集起来并进行实时的建图。
在路径规划的过程中,为了区分环境中哪些部分是可以通行的,哪些部分是不能通行的,我们一般会使用栅格地图。它会将一个区域分成非常多的小的栅格,然后在每一个栅格中放一个binary values (0 or 1, 0 means free; 1 means occupied),如下图所示:
上图表示在已知的地图中进行栅格地图的构建,那么怎么在未知的环境中利用传感器信息构建栅格地图呢
在实际中,传感器的测量量通常是有噪声的且不确定的(noisy and uncertain)。在某些情况中,传感器对一个栅格上一个时刻的观测与下一个时刻的观测很有可能会不同,例如上一个时刻传感器观测该栅格是障碍物,而下一个时刻传感器发现该栅格是free的。那么怎么解决这个问题呢?
我们使用一个binary random variables(二值随机变量),基于对某一个栅格之前的已存在的所有的观测,去计算这个栅格的状态的后验概率。
Notation Definition
For a grid ![]() in occupancy grid map,
in occupancy grid map,
• the probability of the grid state being occupied: ![]() , called
, called ![]() ,
,
• the probability of the grid state being free : ![]() , called
, called ![]() ,
,
note that ![]() = 1 -
= 1 - ![]() . 对一个栅格要说其状态要么是occupied要么是free。
. 对一个栅格要说其状态要么是occupied要么是free。
For observations z,
• the observation that we get at the -th time is denoted as ![]() . 对第t次的观测将其记为
. 对第t次的观测将其记为![]() 。
。
Calculate the posterior probability of the grid state based on existing observations. 我们要基于当前对于该栅格状态已有的全部观测计算其当前状态的后验概率,即我们要求的是下式:
![]() 和
和 ![]()
其中:![]() 表示
表示 ![]() ,
, ![]() ,
, ![]() , ... ,
, ... , ![]() ,
, ![]() , can also be written as
, can also be written as ![]() ,
, ![]() 。
。
Bayesian Filter
The probability of the grid state being occupied
对上述公式进行贝叶斯展开:
Bayes Formula:
以上贝叶斯展开公式可能比较难以理解,那么我们可以先写成:
在公式中加入条件![]() ,得到下式:
,得到下式:
由于![]() 可以写成
可以写成![]() ,故得到贝叶斯展开公式。
,故得到贝叶斯展开公式。
接下来对公式中的![]() 进行马尔可夫假设:
进行马尔可夫假设:
马尔可夫假设:每一次的观测都是独立的,前面的观测与本次观测不互相影响。
再对公式中的![]() 进行贝叶斯展开:
进行贝叶斯展开:
根据以上公式,很容易写出当grid处于occupied时的后验概率:
观察上两式等号左边的![]() 和等号右边的
和等号右边的![]() ,说明公式隐含了一个更新的关系,每一次是基于第t次的观测
,说明公式隐含了一个更新的关系,每一次是基于第t次的观测![]() 对概率进行更新。
对概率进行更新。
将上两式相除:
整理得:
左右两边同时套上![]() 函数:
函数:
为了使等式简便,我们将等式左边记为![]() ,将等式右边进行
,将等式右边进行![]() 展开:
展开:
上式中的![]() 并没有观测值作为条件,所以它是
并没有观测值作为条件,所以它是![]() 状态的先验,将先验记为
状态的先验,将先验记为![]() 。
。
而![]() 代表一个逆传感器模型(inverse sensor model),介绍逆传感器模型前,先介绍传感器模型(sensor model)。传感器模型
代表一个逆传感器模型(inverse sensor model),介绍逆传感器模型前,先介绍传感器模型(sensor model)。传感器模型![]() 指的是基于当前栅格的状态得到的本次观测值是0或1的概率;而逆传感器模型
指的是基于当前栅格的状态得到的本次观测值是0或1的概率;而逆传感器模型![]() 概念并不直观,所以再次使用贝叶斯公式将逆传感器模型的公式展开:
概念并不直观,所以再次使用贝叶斯公式将逆传感器模型的公式展开:
![]()
![]()
即:
代入初始等式中整理到一个新的递推更新公式:
根据上文的定义,有:
![]()
grid is observed as occupancy:

在很多时候我们会进行假设,假设传感器模型![]() 不会发生变化,所以
不会发生变化,所以![]() 和
和![]() 均为定值,所以在以下的状态递推更新公式中:
均为定值,所以在以下的状态递推更新公式中:
我们就可以用简单的加减法来更新栅格状态,更新的效率非常高。
由于我们关心的是后验概率,而以上都是在对![]() 进行操作,那么对于
进行操作,那么对于![]() ,有:
,有:
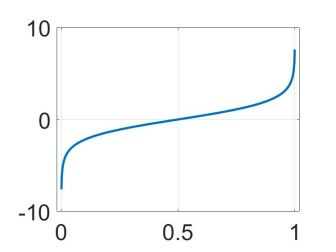
简化为:
可见随着x的增长,f(x)的值单调的从负无穷上升至正无穷,即随着![]() 的增长,
的增长,![]() 不断增大。说明如果我们对后验概率设定一个阈值(如0.5),然后规定当
不断增大。说明如果我们对后验概率设定一个阈值(如0.5),然后规定当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。于是通过上图可以知道在我们的规定下:当
。于是通过上图可以知道在我们的规定下:当![]() 时
时![]() ,当
,当![]() 时
时![]() 。于是就找到了一个后验概率和
。于是就找到了一个后验概率和![]() 的对应关系。
的对应关系。
Octo-map 八叉树地图
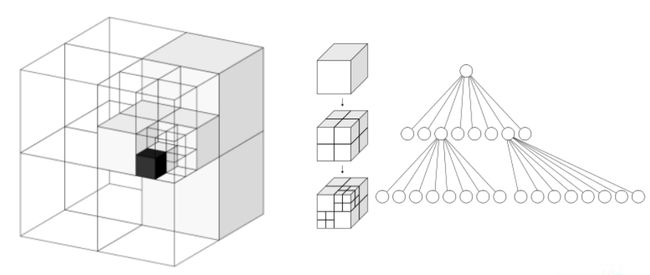
在栅格地图中存在大片空白区域(没有障碍物)时,此时没有必要进行密集的切分,于是八叉树地图就成为了解决方法之一。
八叉树地图来源于八叉树数据结构,一个父节点有八个子节点。环境中没有障碍物的地方,如上图左一左上角可以用一个方块来表示,而当某个大方块中有障碍物时就递归的切分下去,直到切到最小的包含障碍物的部分为止。
Sparse 稀疏的,它无需进行稠密的对环境空间的切分
Structural 方块排列非常整齐,具有结构化的特征
Indirect Index Query 进行非直接的查询,它要通过八叉树的结构进行递归的查询而非直接通过索引
https://octomap.github.io/
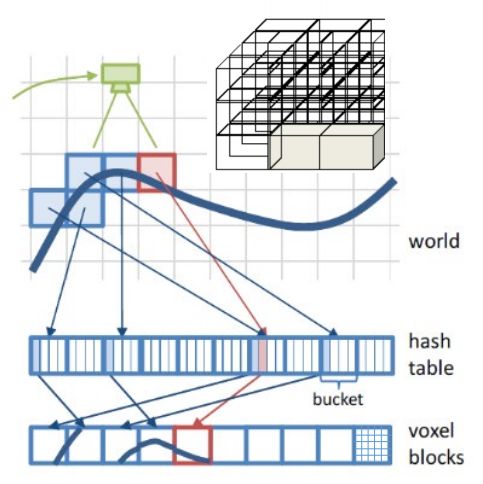
Voxel hashing 使用哈希表存储的voxel地图
与八叉树地图思路相近,voxel指的是三维的grid。
上图表示相机对障碍物一个曲面的观测,我们只会将在观察到了通过了该曲面而受到影响的格子加入到内存中。加入内存的方式与上述两者不相同,它并不像Occupancy grid map和Octo-map在内存中是按照很好的规则排列下来的,而是离散的在内存中排列,于是为了访问它就需要用到哈希表(哈希函数)。
值得一提的是,该地图并不是将每一个voxel都哈希地存储起来,而是分为blocks和voxel,voxel是最精细的小的栅格,上图中一个blocks由5×5×5个voxel组成,将blocks用哈希表的形式存储起来。所以在具体访问时我们输入一个坐标或者其他信息,计算出我们要访问的坐标或信息在哪个blocks中,再通过得到的blocks坐标计算其对应的哈希键值,在内存中将其提取出来,再在提取出来的blocks中精细的访问voxel。
Most Sparse 最稀疏的地图,可用于基于RGB-D相机的三维重建或SLAM中
Structural
Indirect Index Query
https://github.com/niessner/VoxelHashing
Point Cloud Map 点云地图
点云地图是传感器原始测量(raw measurement)的一个集合,是无序地图。
Un-ordered
No Index Query 无序地图,无法进行根据索引的查询
点云可用来表示非常稠密的障碍物的信息。
PCL库: http://pointclouds.org/
TSDF map
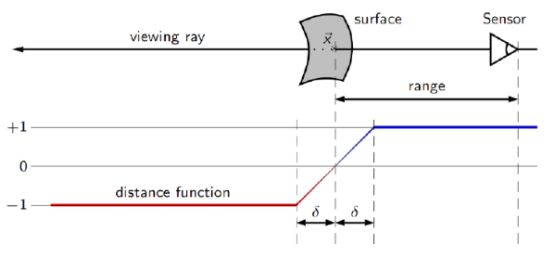
Truncated Signed Distance Functions 截断的有符号距离函数
假设如上图所示,有一个相机正在对环境(一个曲面)进行观测,相机与障碍物之间有一个距离场,距离场中的每一个值都是正值,里面的值表示某一点与其最近的障碍物(曲面)之间的距离。会认为障碍物外部的值是正的,而内部的值是负的,如上图所示,蓝色表示距离为正值,红色表示距离为负值。
TSDF的含义,Truncated表示不需要维护整个地图中所有的点的距离场的值,例如上图只维护相机视锥的扇形区域内的距离场的值,且会进行一个截断,例如离相机3米以内的值是我关心的,需要进行维护,而两米外的扇形区域就无需进行维护了。
https://github.com/personalrobotics/OpenChisel
ESDF map
Euclidean Signed Distance Functions 欧式带符号的距离函数
ESDF表示不进行截断,即下图里包括所有灰色区域的距离函数都进行维护。
需要知道全图的距离信息才可以做Soft constraint Minimum-snap。
最后得到如下图:
其中越趋近红色表示离障碍物越近,绿色区域表示安全区域。
https://github.com/ethz-asl/voxblox
https://github.com/HKUST-Aerial-Robotics/FIESTA
https://github.com/HKUST-Aerial-Robotics/Teach-Repeat-Replan
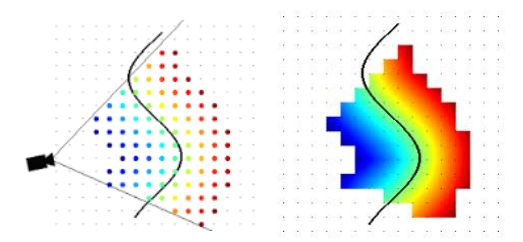
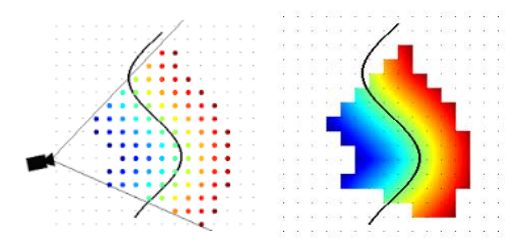
Map Comparison
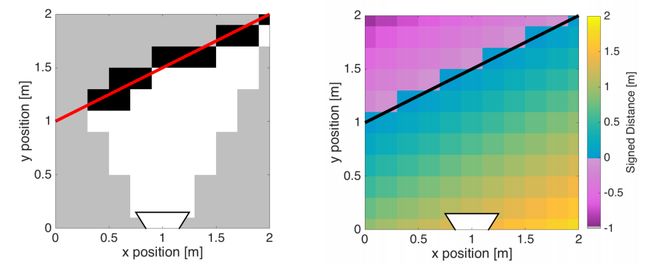
Left: Occupancy representation, where each cell is either labelled as occupied or free.
Right: ESDF, which represents the Euclidean distance to the surface at each cell.
左边的地图的灰色部分就是未观测的部分,白色部分是观测到free的区域,黑色部分是观测到occupied的区域。
右边的ESDF地图存放的是到最近的障碍物分界面的距离,在障碍物里面的ESDF值为负。
ESDF有很多种的建立方法:可以基于grid map、TSDF建立,可以增量式(incremental update)或者批量式(generation in batch)地建立。
ESDF generation in batch from grid map
为什么使用批量式生成ESDF呢?
在导航之中,特别是某些局部规划的框架中(比如Fast-planner),每一次规划的区域都比较小。如果采用增量式的方法,首先在内存开销上并没有这个必要,其次是增量式的方法虽然速度更快,但是在实现上没有直接批量式生成地图方便。
先不考虑符号的概念:
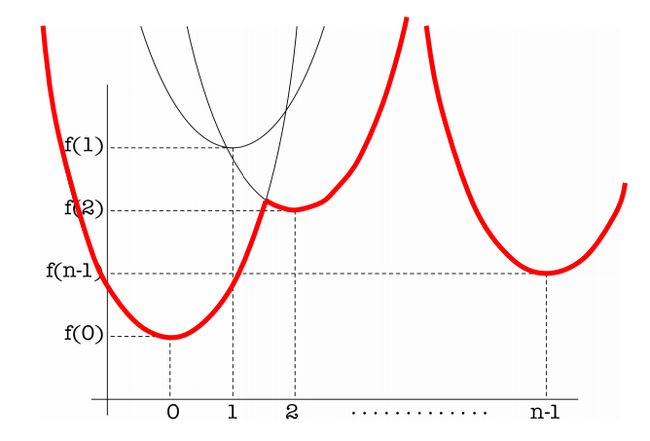
在横轴上的每一个整数的位置放一个二次函数:![]()
p表示横轴的横坐标,n表示其所在的每一个整数,f(n)表示对二次函数的纵轴的值上移的量。
我们希望在这些二次抛物线中找到随着p变化的最小函数值组成的函数(即下包络线)。
那么这个和我们构建ESDF有什么关系呢?以一个一维地图为例:
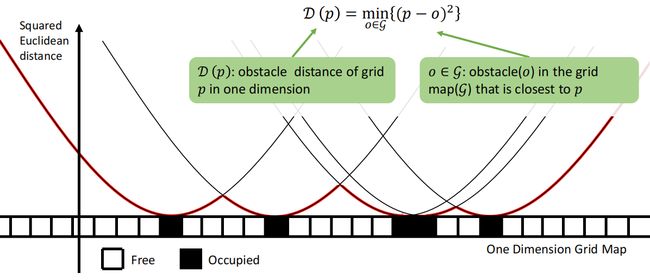
一维地图就是像上图这样一行一行的栅格地图。如果在一维栅格地图中有一个障碍物,那么其他栅格到这个栅格的距离可以用一个二次函数来表示,多个障碍物就会对应多条二次函数曲线。多条二次函数曲线的下包络线的意义就很明显了:每个栅格到距离它最近的障碍物的距离的平方。
取下包络线的行为可以写成:![]() ,其中
,其中![]() 表示地图中所有的障碍物。
表示地图中所有的障碍物。
将![]() 写成更加通用的形式:
写成更加通用的形式:
![]()
![]() 在一维地图中作用可能不大,但是在高维ESDF中会起到作用。
在一维地图中作用可能不大,但是在高维ESDF中会起到作用。
注意,定义距离变换的任意两条抛物线只会有一个交点,我们可以通过简单的代数运算得到栅格位置p和q的抛物线相交的水平位置:
![]()
化简得:
那么![]() 函数该怎么计算呢?给出计算
函数该怎么计算呢?给出计算![]() 的伪代码(针对一维栅格地图):
的伪代码(针对一维栅格地图):
高维地图该怎么进行处理呢?
首先我们将:
![]()
从一维推广到二维:
![]()
![]() 和
和![]() 对应了一维公式中的q,上式中等号右侧的第一项与
对应了一维公式中的q,上式中等号右侧的第一项与![]() 无关,所以我们可以将等式写成:
无关,所以我们可以将等式写成:
![]()
固定![]() 后,
后,![]() 就只与
就只与![]() 有关,相当于把二维先转化成了一维的情况:
有关,相当于把二维先转化成了一维的情况:
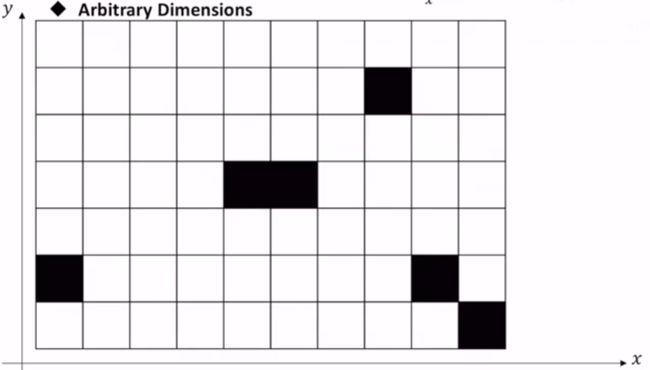
来看一个二维的栅格地图:
我们有:
![]()
只看![]() 部分,先将
部分,先将![]() 置为零,那么就此时求这部分就相当于求一维栅格地图的
置为零,那么就此时求这部分就相当于求一维栅格地图的![]() (可将
(可将![]() 看作
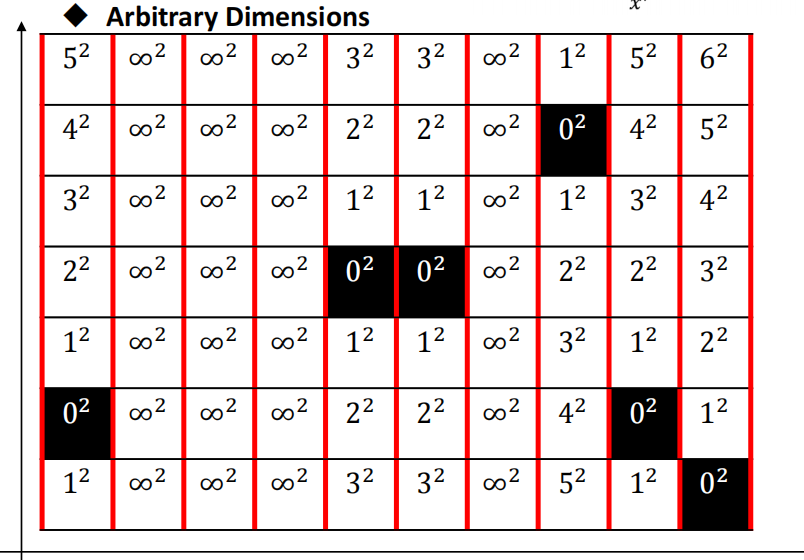
看作![]() 中的o)。其实际意义为上图中一列一列的一维栅格地图求距离,一列一列的计算一维地图中的下包络,如下图所示:
中的o)。其实际意义为上图中一列一列的一维栅格地图求距离,一列一列的计算一维地图中的下包络,如下图所示:
图中无穷大表示该列中没有障碍物,看作障碍物在无穷远处。
所以在只考虑等式右边第二项时就变成了一维的形式,接下来看整个函数:
![]()
可以写成:
![]()
单看![]() 将每个栅格中都赋了一个初始值,即上式中的
将每个栅格中都赋了一个初始值,即上式中的![]() 已经有了值。
已经有了值。
那么考虑一行一行的栅格中的值,已经与![]() 值没有关系了,因为
值没有关系了,因为![]() 对
对![]() 的影响已经提前给定值了,
的影响已经提前给定值了,![]() 不再成为以行标准的自变量了,
不再成为以行标准的自变量了,![]() 此时只取决于
此时只取决于![]() ,于是式子可以写成:
,于是式子可以写成:
![]()
相当于一行中的每一个栅格都是一个障碍物,现在要算的距离不仅仅是到障碍物的距离![]() ,还要加上障碍物栅格中存的值
,还要加上障碍物栅格中存的值![]() 。同时上式并没有违背
。同时上式并没有违背![]() 的形式。
的形式。
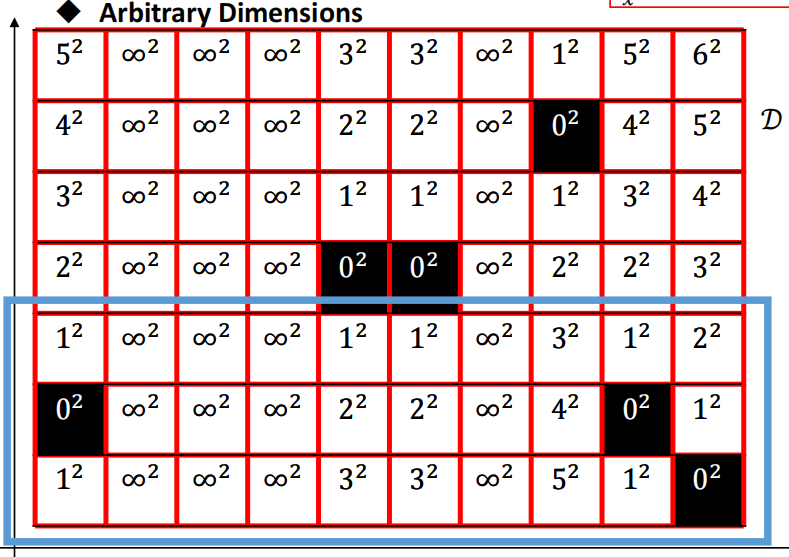
一行一行的划分二维栅格地图:
取最后三行: