【机器学习】多元梯度下降法

（本文略过了原课程中线性代数部分内容，如果你不理解线性代数，那你应当先去学习线性代数相关知识）

上一章——梯度下降

---

多元假设方程

在第二章中，我们给出了线性回归的一元线性假设方程
一元线性假设方程:$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

然而在实际情况中，我们不可能只有一个特征，比如房子的价格不仅由Size决定，其影响因素还有房间数量、房龄、地段等等特征，因此我们要将学习过的知识从一元推广到多元。

n 代表了特征的数量
$x^{(i)}$代表第i行的训练样本，我们可以用一个列向量表示改行
$x_j^{(i)}$代表第i行，第j列的元素
$y$为我们所求的预测值
那么在上列训练集中，有四个特征，因此我们可以列出如下的
四元线性假设方程：
$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+{\theta }_4{x}_4$
n元的依此类推：
$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+......+{\theta }_n{x}_n$
让我们令$x_0=1$,得到这个式子
$h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+......+{\theta }_n{x}_n$
那么令 θ = [ θ 0 θ 1 θ 2 . . . θ n ] θ=\begin{bmatrix*}[r] θ_0 \\θ_1\\θ_2\\...\\θ_n \end{bmatrix*} θ= ​θ0​θ1​θ2​...θn​​ ​令 x = [ x 0 x 1 x 2 . . . x n ] x=\begin{bmatrix*}[r] x_0 \\x_1\\x_2\\...\\x_n \end{bmatrix*} x= ​x0​x1​x2​...xn​​ ​
则$h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+......+{\theta }_n{x}_n={\theta }^{T}x$
所以$h_{\theta }(x)={\theta }^{T}x$

---

多元梯度下降

多元梯度下降公式

同理我们可以将梯度下降，代价函数等也推广到多元
多元代价函数:$J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
或$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$[$J(\theta )$中θ代表向量 θ = [ θ 0 θ 1 θ 2 . . . θ n ] θ=\begin{bmatrix*}[r] θ_0 \\θ_1\\θ_2\\...\\θ_n \end{bmatrix*} θ= ​θ0​θ1​θ2​...θn​​ ​]
而梯度下降公式：${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$
比如${\theta }_0:={\theta }_0-\alpha \frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$
${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$
(对$J(\theta )$求${\theta }_j$的偏导后，得到$2\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$,最终变为上式，其中$x_0^{(i)}=1$)

---

特征归一化

之前在写代价公式的时候提到了，为什么我们要乘以一个$\frac{1}{2m}$,看起来似乎并没有必要，这是由于我们需要对数字进行归一化处理，来保证它们在可接受的大小范围内
一个简单的例子，假如我们取下列的数据，$x_1$的范围是$[0,2000]$,$x_2$的范围是$[1,5]$，那么画出来的图将如下

由于我们在纵轴上的范围更大，横轴上的范围小，这就导致画出的等高线图像是一个瘦长的椭圆形，
如果我们想要在这个图上进行梯度下降的话，对于这种又瘦又高的图像，梯度下降时则会在图像的左右两侧来回震荡，
最终晃晃悠悠地接近最低点，这就导致需要花费更长的时间来进行计算

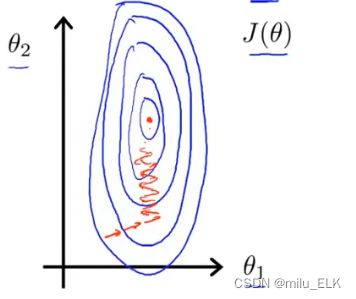
因此，我们的解决方法是将数据进行归一化，进行特征缩放
将每个特征除以区间大小，再绘制图像

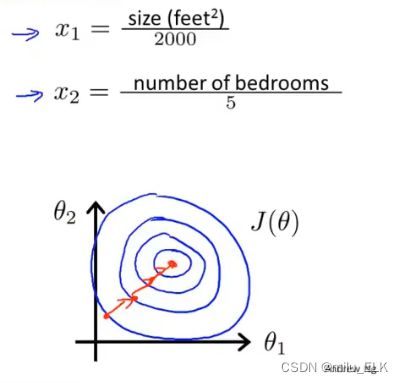
可以看到在新的图像中，梯度下降变得更加敏捷、有效。
归一化公式:
$x_i:=\frac{x_i-{\mu }_i}{S_i}$，其中${\mu }_i$代表特征值的平均值，$S_i$代表特征值的范围大小
总得来说，一般要求特征范围在$-1\le x_i\le 1$内
在实际中$-3\le x_i\le 3$，$-\frac{1}{3}\le x_i\le \frac{1}{3}$内都是可以接受的

---

学习率对代价函数图像的影响

之前在学习梯度下降的公式时我们就知道学习率对梯度下降的影响了
那么在选择学习率的过程中，如何确定适宜的学习率呢，我们可以通过对代价函数的图像观察来得出结论。

上图是一个学习率适宜时，以迭代次数为横轴，代价函数大小为纵轴的图像，我们可以清楚的看到：如果学习率选择正确，那么代价函数$J(\theta )$应当不断变小，并且随着迭代次数的增加，代价函数会趋近于0，当迭代次数足够多时，曲线趋于平坦，意味着函数收敛了。但是我们不知道它可能在何时收敛，也许需要迭代3千次，或者3万次，甚至30万次才能收敛，不过好在我们也有判断收敛的方法，我们可以用自动收敛算法来判断，或者给出一个定值η，当小于这个定值η时认为它收敛了。

如果图像呈现上升的趋势，说明梯度下降算法没有正常运行，这是由于学习率过大，在这种情况下我们就应该降低学习率

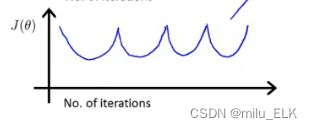
或者有可能由于学习率取得不对，导致图像呈现周期性。

在测试最佳学习率的时候，我们可以每隔十倍取一次数，比如100，10，1，0.1，0.01…或者每隔三倍，来寻找最佳学习率。

---

下一章——正规方程