卷积神经网络学习——第一部分：认识并搭建两层卷积神经网络

---

一、序言

   本文基于北邮数据科学基础课程的期中作业和相关课件知识，以Pytorch环境为基础，实现两层卷积神经网络，并针对各个参数进行推导和演算。本文目标：

1. 巩固知识 ，掌握机器学习的相关基础知识，主要包含课件上卷积层、激活层等内容；
2. 强化流程，掌握常规机器学习流程，并对模型中的部分参数进行修改，了解参数的意义；
3. 薪火相传，帮助后来的学弟学妹们能更好地理解课程的知识，更好上手（但部分代码会隐去，不会给你们抄代码的机会）

   整个模型的实现包括：构建网络、训练模型和模型评估三个部分，分别对应了网络结构、学习策略和评价指标三个部分的对应知识。本部分，将主要从网络的研究和实现开始，详细阐述参数以及函数设置的意义。
   由于笔者确实是太忙太忙了，所以只能想到什么就先更新什么了～慢慢更新也是慢慢学习的过程（万一以后真的去了数据科学相关的实验室呢）

——2020年11月19日于北邮教三333

二、网络实现

1、模型构建

   现在先构建我们所需要的两层卷积神经网络模型了。那么在构建之前，我们需要思考卷积神经网络一共有几个函数。这里我们以课件上给出的模型为例，进行注意地研究其中函数和参数对应的意义。

class ConvNet(nn.Module):
    # 课件上的代码
    def __init__(self):
        super().__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, 5)
        self.conv2 = torch.nn.Conv2d(10, 20, 3)
        self.fc1 = torch.nn.Linear(20*10*10, 500)
        self.fc2 = torch.nn.Linear(500, 10)
    def forward(self, x):
        in_size = x.size(0)
        # 卷积层 -> Relu -> 最大池化
        out = self.conv1(x)
        out = F.relu(out)
        out = F.max_pool2d(out, 2, 2)
        # 卷积层 -> Relu
        out = self.conv2(out)
        out = F.relu(out)
        # 多行变一行 -> 全连接层 -> relu -> 全连接层 -> sigmoid
        out = out.view(in_size, -1)
        # 全连接层 -> Relu
        out = self.fc1(out)
        out = F.relu(out)
        out = self.fc2(out)
        out = F.log_softmax(out, dim = 1)
        return out

2、类和函数的意义及性质

（1）nn.Conv2d

   Conv2d类完整地参数如下所示：

nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)

   其对应有较多的参数，在本文中我们重点研究前三个参数，这些是限制我们的主要因素。我们会在下一个函数中重点讨论参数修改的意义。而单独看这里的代码，几个参数都属于是根据需求自定义的部分。

in_channels	输入通道数，也就是当前层的深度
out_channels	输出通道数，也就是输出的深度
kernel_size	卷积核尺寸

   Conv2d是一个针对2d的卷积神经网络生成的类，其作用是生成一个输入通道与输出通道对应的卷积神经网络，并通过卷积核（默认步长为1）对图像进行再输出。其作用机理如下：

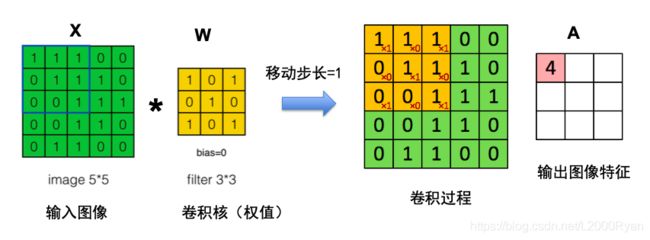
   从图中来看，我们可以发现，每当图像进行了一次卷积之后，它的输出都发生了对应的改变。如图所示，其输入为5x5，在尺寸为3x3的卷积核和1的步长作用下，最后得到的输出图像特征的尺寸不再是5，而是5-3+1=3。所以经过了卷积层之后，其实他的输出尺寸都会发生相应的变化。

（2）F.max_pool2d

   F.max_pool2d类完整地参数如下所示：

F.max_pool2d_with_indices(input, kernel_size, stride)

input	输入
kernel_size	最大池化的窗口大小
stride	步长

   F.max_pool2d是用于对特征矩阵进行池化滤波的一个类。除此之外，nn当中的MaxPool2d类也可以起到同样的效果。其最大池化的原理示例如下：





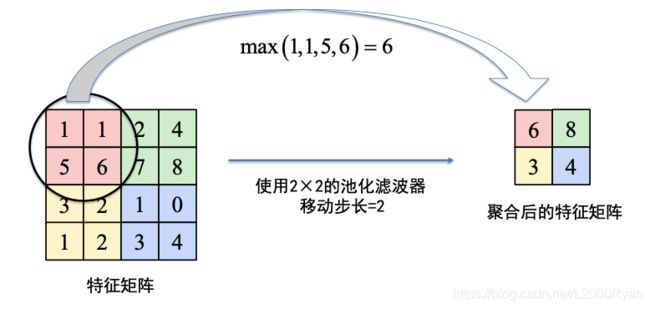
   我们可以看到最大池化后会和卷积后一样，使得特征矩阵大小发生变化。这里需要记住的是，其发生变化的大小和窗口大小有关。

（3）F.relu

   F.relu就是一个非线性激励函数，在这里选择的就是relu作为非线性激活函数。它有很多好处和劣势，但是用的比较广，可以参考这篇文章进一步了解它的特性：relu的作用
   比较常有的问题还包括：为什么relu要在conv1之后？这个主要是由于细胞体的整体结构决定的，对于一个完整的神经网络来说，卷积和激活函数一起组成了这一层神经元。并且其可以极大增加泛化处理的能力。

（4）F.log_softmax

   F.log_softmax一般是应用在网络的输出层，做一个回归的处理，其本质也是一个特殊的激活函数。
   这里需要理解一下为什么是回归和应用。首先，我们在做分类问题的时候，其本质是一个概率问题：它大概率属于哪一类。但是我们的卷积神经网络的输入和输出都只是一个或者多个具体的值，而不是一个概率。所以需要用一个激活函数将这个值与某一个概率p映射对应起来。
   我们的卷积神经网络用来解决分类问题时，就是先通过卷积层得到特征X，之后通过classifier得到WX+b，再通过Sigmoid、logSoftmax或者Softmax函数得到概率p，最后根据最大概率p得到类别。所以在这里，并不仅仅只有这个函数可以。也可以换做是其他的函数，但是总的来说，卷积神经网络的输出层需要一个非线性函数将值与概率分布联系起来，这样才能完成分类的问题。
   如果你还是有些不太明白，那么你可以参考链接：神经网络输出层为什么通常使用softmax?、为什么神经网络架构搜索darts采用了softmax实现由离散到连续的转换？和多类分类下为什么用softmax而不是用其他归一化方法?进一步了解一下。如果你选择的优化器为交叉熵优化器，那可以看一下softmax loss详解，softmax与交叉熵的关系进一步了解一下它们两者之间的关系和使用时的注意事项。

（5）nn.Linear

   Linear类完整地参数如下所示：

nn.Linear(in_features, out_features, bias=True)

in_features	输入的大小
out_features	输出的大小

   torch.nn.Linear是最麻烦的一个类，他的参数也是本文主要想要研究清楚的地方。它是用于设置全连接层的。但是全连接层的输入与输出都是二维张量，一般形状为[batch_size, size]，不同于卷积层要求输入输出是四维张量。那么为了达成这种平衡，就会用到view函数，将原来的数据降维成一个一位列向量。不然，在这里是无法正常使用的。
   由于现在已经是一维列向量了，所以输入就需要是其中的某一个sample的大小。已经在这里为了方便大家更好地理解大小这一回事，我们需要再次认识一下卷积神经网络。
   首先，在这里的卷积神经网络不是一个二维网络，他是一个三维网络，包含了原始的二维数据以及各层中输入的通道数（也即是深度）。所以，我们往往会采用的 深度x高度x宽度 的形式来表示输入的大小。那我们再来看代码，我们会发现，这个里面的参数是 20x10x10。20很好理解，20是Conv2的输出通道数，就是此时的深度。但是为什么是 10x10 来表示此时的 高度x宽度 呢？按照我们的理解，此时输入的图像大小应该为 28x28 ，而不应该是 10x10 。
   为了理解10的来历，首先我们要再回顾基础知识中卷积核的相关内容。

   从本图来进行理解，我们会发现，每当图像经过一次处理，它的尺寸都会发生相应的变化。这个变化只与卷积核大小、步长还有图像本身大小有关。从这张图来看，我们可以发现它的放缩满足 L图-L核+1 这样的一个规律。
   也就是说，输入到Linear时，图像的尺寸已经不是28x28了。此时从网络结构上来看，已经经过了两次卷积和一次池化。池化的作用同理可见。所以10其实是计算后的结果，计算的方式为：

1. 第一次卷积（卷积核为5）：28-5+1=24
2. 第一次池化（池化滤波器为2）：24/2=12
3. 第二次卷积（卷积核为3）：12-3+1=10

   到这里也差不多就破案了，所以我们可以概括出来第一次Linear时，其输入参数为 深度x高度x宽度 。其中深度为最后一个卷积层输出的通道数，高度和深度都是根据过程中经历过的卷积和池化的次数计算得来的。

3、模型总结

   现在概括一下我们之前提到的这些函数以及步骤，我们可以用nn.Sequential函数对每一层进行重构，使得结果更加直观：

class ConvNet(nn.Module):
    def __init__(self):
        super(ConvNet, self).__init__()
        self.conv1 = nn.Sequential(
            nn.Conv2d(1, 10, 5),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2)
            )
        self.conv2 = nn.Sequential(
            nn.Conv2d(10, 20, 3),
            nn.ReLU()
            )    
        self.fc = nn.Sequential(
            nn.Linear(20 * 10 * 10, 500),
            nn.ReLU(inplace=True),
            nn.Linear(500, 10)      
            )

    def forward(self, x):
        in_size = x.size(0)
        out = self.conv1(x)
        out = self.conv2(out)
        out = out.view(in_size, -1)
        out = self.fc(out)
        out = F.log_softmax(out, dim = 1)
        return out

   从这样的一个新的网络结构来看，其实搭建一个卷积神经网络只需要满足：确定层数、按照卷积、激活以及是否需要池化等方式定义每一层、层与层之间输入输出匹配这几点，就能够实现一个卷积神经网络的搭建了。

三、总结

   写到这里已经写了三四个小时了，因为也是对机器学习慢慢加深理解的过程，所以可能有些地方用词不够严谨。也希望如果有我做的不太好的地方可以留言一起研究，一起更改。希望能够在期末考完之前更完所有～