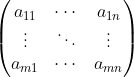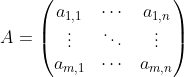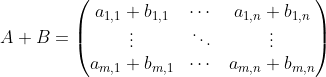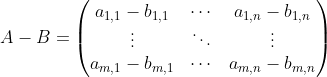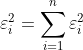（机器学习的矩阵）（向量、矩阵与多元线性回归）
机器学习的矩阵
等公交车时我们期待大家要排队，如果 将人改为数字，也就是数字排队，这个就是矩阵（matrix）。
矩阵的表达方式
矩阵的行与列
矩阵是由row和clo(column的简写)组成。
row翻译为行，col翻译为列。
矩阵中m代表行（row），n代表列（column）。
矩阵变量名称
矩阵的变量名称常用大写英文字母表示，下列是设定矩阵的变量名称是A。
常见的矩阵表达方式
其它矩阵表达方式：
矩阵元素表达方式
矩阵元素常用下标表示，可以参考下列书写方式：
i是行号，j是列号。
矩阵相加与相减
基础概念
有2个矩阵如下：
矩阵相加或相减，相当于相同位置的元素执行相加或是相减，所以不同大小的矩阵无法执行相加减，如下所示：
矩阵加减运算的交换律与结合律是成立的。
交换律：A+B=B+A
结合律：(A+B)+C=A+(B+C)
Python实践
定义矩阵可以使用numpy的matrix()方法，有一个矩阵如下：
>>> import numpy as np
>>> A=np.matrix([[1,2,3],[4,5,6]])
>>> A
matrix([[1, 2, 3],
[4, 5, 6]])
>>>矩阵相加与相减的应用
import numpy as np
A = np.matrix([[1, 2, 3], [4, 5, 6]])
B = np.matrix([[4, 5, 6], [7, 8, 9]])
print('A + B = {}'.format(A + B))
print('A - B = {}'.format(A - B))
运行结果如下：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
A + B = [[ 5 7 9]
[11 13 15]]
A - B = [[-3 -3 -3]
[-3 -3 -3]]
[Done] exited with code=0 in 4.159 seconds矩陈乘以实数
矩阵可以乘以实数，操作方式是每个矩阵元素乘以该实数，下列是将矩阵乘以实数k的实例。
矩阵乘以实数的交换律、结合律与分配律是成立的。
交换律：kA=Ak
结合律：jkA=j(kA)
分配律：(j+k)A=jA+kA
k(A+B)=kA+kB
矩阵乘以2。
import numpy as np
A = np.matrix([[1, 2, 3], [4, 5, 6]])
print('2 * A = {}'.format(2 * A))
print('0.5 * A = {}'.format(0.5 * A))运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
2 * A = [[ 2 4 6]
[ 8 10 12]]
0.5 * A = [[0.5 1. 1.5]
[2. 2.5 3. ]]
[Done] exited with code=0 in 4.375 seconds矩阵乘法
矩阵相乘很重要一点是，左侧矩阵的列数与右侧矩阵的行数要相同，才可以执行矩阵相乘。
乘法基本规则
A矩阵是
，B矩阵是
使用numpy模块，可以使用*或是@运算符执行矩阵的乘法。
import numpy as np
A = np.matrix([[1, 2], [3, 4]])
B = np.matrix([[5, 6], [7, 8]])
print('A * B = {}'.format(A * B))
C = np.matrix([[1, 0, 2], [-1, 3, 1]])
D = np.matrix([[3, 1], [2, 1], [1, 0]])
print('C @ D = {}'.format(C @ D))运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
A * B = [[19 22]
[43 50]]
C @ D = [[5 1]
[4 2]]
[Done] exited with code=0 in 2.09 seconds乘法案例
下表是甲和乙要购买水果的数量：
| 名字 | 香蕉 | 芒果 | 苹果 |
| 甲 | 2 | 3 | 1 |
| 乙 | 3 | 2 | 5 |
下表是超市与百货公司的水果价格：
| 水果名称 | 超市价格 | 百货公司价格 |
| 香蕉 | 30 | 50 |
| 芒果 | 60 | 80 |
| 苹果 | 50 | 60 |
计算甲和乙在超市和百货公司购买各需要多少金额。
import numpy as np
A = np.matrix([[2, 3, 1], [3, 2, 5]])
B = np.matrix([[30, 50], [60, 80], [50, 60]])
print('A * B = {}'.format(A * B))
运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
A * B = [[290 400]
[460 610]]
[Done] exited with code=0 in 2.403 seconds假设各式水果热量如下：
| 水果 | 热量 |
| 香蕉 | 30卡路里 |
| 芒果 | 50卡路里 |
| 苹果 | 20卡路里 |
甲和乙各吃数量如下，计算会产生多少卡路里。
| 名字 | 香蕉 | 芒果 | 苹果 |
| 甲 | 1 | 2 | 1 |
| 乙 | 2 | 1 | 2 |
代码如下：
import numpy as np
A = np.matrix([[1, 2, 1], [2, 1, 2]])
B = np.matrix([[30], [50], [20]])
print('A * B = {}'.format(A * B))运行结果如下：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
A * B = [[150]
[150]]
[Done] exited with code=0 in 2.34 seconds矩阵乘法规则
矩阵运算时，结合律和分配律是成立的。
结合律：
分配律：
矩阵运算时，交换律是不成立的。
不等于 
验证 不等于
代码如下：
import numpy as np
A = np.matrix([[1, 2], [3, 4]])
B = np.matrix([[5, 6], [7, 8]])
print('A * B = {}'.format(A * B))
print('B * A = {}'.format(B * A))
运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
A * B = [[19 22]
[43 50]]
B * A = [[23 34]
[31 46]]
[Done] exited with code=0 in 4.095 seconds
方形矩阵
一个矩阵如果行数（row）等于列数（column），方形矩阵（square matrix）。
单位矩阵
一个方形矩阵如果从左上到右下对角线的元素皆是1，其它元素皆是0，这个矩阵称单位矩阵（identity matrix）。
单位矩阵有时用大写英文E或I表示。
单位矩阵就类似阿拉伯数字1，任何矩阵与单位矩阵相乘，结果皆是原来的矩阵。
验证与单位矩阵相乘结果不变。
import numpy as np
A = np.matrix([[1, 2], [3, 4]])
B = np.matrix([[1, 0], [0, 1]])
print('A * B = {}'.format(A * B))
print('B * A = {}'.format(B * A))
运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
A * B = [[1 2]
[3 4]]
B * A = [[1 2]
[3 4]]
[Done] exited with code=0 in 2.165 seconds反矩阵
基础概念
只有方形矩阵（square matrix）才可以有反矩阵（inverse matrix），一个矩阵乘以它的反矩阵，可以得到单位矩阵E，可以参考下列概念。
或是 
如果一个的矩阵，它的反矩阵公式如下：
反矩阵另一个存在条件是
不等于0。下列是一个矩阵A与反矩阵
的实例。
Python实践
导入numpy模块，可以使用inv()方法计算反矩阵。
import numpy as np
A = np.matrix([[2, 3], [5, 7]])
B = np.linalg.inv(A)
print('A_inv = {}'.format(B))
print('E = {}'.format((A * B).astype(np.int64)))运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
A_inv = [[-7. 3.]
[ 5. -2.]]
E = [[1 0]
[0 0]]
[Done] exited with code=0 in 4.747 seconds用反矩阵解联立方程式
假设有一个联立方程式如下：
将上述联立方程式使用下列矩阵表达。
的反矩阵是
，在等号两边乘以相同的反矩阵，可以得到下列结果。
推导可以得到下列结果。
可以得到上述联立方程式的解是x=3，y=-2。
使用反矩阵概念验证上述执行结果 。
import numpy as np
A = np.matrix([[3, 2], [1, 2]])
A_inv = np.linalg.inv(A)
B = np.matrix([[5], [-1]])
print('{}'.format(A_inv * B))运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
[[ 3.]
[-2.]]
[Done] exited with code=0 in 2.025 seconds张量
张量是数学的堆栈结构。
张量用轴空间表示。
标量则是0轴张量，向量称1轴张量，矩阵称2轴张量，3维空间称3轴张量。
定义3维数据，同时使用shape()方法列出数据外形。
import numpy as np
A = np.array([[[1, 2],
[3, 4]],
[[5, 6],
[7, 8]],
[[9, 10],
[11, 12]]])
print('{}'.format(A))
print('shape = {}'.format(np.shape(A)))执行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\ch21_10.py"
[[[ 1 2]
[ 3 4]]
[[ 5 6]
[ 7 8]]
[[ 9 10]
[11 12]]]
shape = (3, 2, 2)
[Done] exited with code=0 in 1.479 seconds转置矩阵
基础概念
转置矩阵的概念就是将矩阵内列的元素与行的元素对调，所以
的矩阵就可以转成的矩阵。
矩阵是A，转置矩阵的表达方式是
Python实践
设计转置矩阵时可以使用numpy模块的transpose()，也可以使用T。
转置矩阵的应用。
import numpy as np
A = np.array([[0, 2, 4, 6],
[1, 3, 5, 7]])
B = A.T
print('{}'.format(B))
C = np.transpose(A)
print('{}'.format(C))运行结果：
[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
[[0 1]
[2 3]
[4 5]
[6 7]]
[[0 1]
[2 3]
[4 5]
[6 7]]
[Done] exited with code=0 in 2.633 seconds转置矩阵的规则
转置矩阵可以再转置还原矩阵内容。
矩阵相加再转置，等于各矩阵转置再相加。
标量c乘矩阵再载转置，与先转置再乘以标量结果相同。
转置矩阵后再做反矩阵，等于反矩阵后转置
矩阵相乘再转置，等于各矩阵转置后交换次序再相乘。
转置矩阵的应用
省略
向量、矩阵与多元线性回归
向量应用在线性回归
单纯的线性方程式如下：
x代表每年的拜访数据，y是每年国际证照的销售数据。如果数据量庞大，收集了n年，则可以使用向量表达此数据。
#下标代表第n年，
是第n年拜访客户次数
#下标代表第n年，
是第n年销售考卷数
由于上述和代入会有误差
，所以可以为误差加上下标，这样误差可以使用误差向量表示：
现在的线性方程式：
现在斜率a与截距b是标量，由于斜率a乘以向量x后会是n维向量，所以必须将标量b改为向量，如下所示：
整个线性方程式执行推导：
使用最小平方法计算误差平方的总和：
误差向量的内积，推导公式：
执行误差平方最小化，等同是计算向量内积：
向量应用在多元线性回归
在多元回归中，习惯会用
当作斜率的系数，截距则用
代替，整个多元回归通式可以使用下列公式表达：
矩阵应用在多元线性回归
省略
将截距放入矩阵
省略
简单的线性回归
省略