Andrew Ng 深度学习课程——改善深层神经网络：超参数调试、正则化以及优化

感谢Andrew Ng的公开课¹，这个博客主要是记录公开课的学习过程与理解。

深度学习实用层面

数据集

数据集被分为了训练集，验证集，测试集。

• 训练集（train set）：用训练集对算法或模型进行训练过程；
• 验证集（development set）：利用验证集或者又称为简单交叉验证集（hold-out cross validation set）进行交叉验证，选择出最好的模型；
• 测试集（test set）：最后利用测试集对模型进行测试，获取模型运行的无偏估计。
  在数据量比较小的时候，通常以7/3或者6/2/2的方式划分数据。在数据量非常大时候（百万级）那么就不再需要那么多的数据做验证和测试了。
• 100万数据量：98% / 1% / 1%；
• 超百万数据量：99.5% / 0.25% / 0.25%（或者99.5% / 0.4% / 0.1%）

偏差(bias)与方差(variance)

评价算法有坏有两个方面，当训练集的准确率不好，验证集的准确率不好时候，就是高偏差状态，也就是机器学习中的欠拟合状态，误差大，这个时候的损失函数的值比较大的；当训练集的准确率高，而验证集的准确率却不理想就是高方差状态（过拟合）。正常的状态是提高训练集的准确率的同时，验证集的准确率也不相上下，就是正好的状态。

改善高偏差状态（欠拟合）：

• 增加网络结构，如增加隐藏层数目；
• 训练更长时间；
• 寻找合适的网络架构，使用更大的NN结构；

改善高方差状态（过拟合）：

• 获取更多的数据；
• 正则化（ regularization）；
• 寻找合适的网络结构；

参数的初始化

神经网络中的参数$W$和$b$是可以做随机初始化的 ，但是$W$不能直接做全零的初始化，会造成网络无法训练，输出的结果全是一样的。可以使用np.random.randn(layers_dims[l], layers_dims[l-1])和np.random.randn(layers_dims[l], 1)分别对$W^{[l]}$和$b^{[l]}$进行随机初始化。还可以使用He initialization的方式进行初始化，

parameters['W'+str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*np.sqrt(2/layers_dims[l-1])
parameters['b'+str(l)] = np.random.randn(layers_dims[l], 1)*np.sqrt(2/layers_dims[l-1])

He initialization对ReLU激活函数适用性非常好。

正则化(regularization)

前面到，正则化是解决高方差的一种方式，正则化是在 Cost function 中加入一项正则化项，惩罚模型的复杂度。先看结果，一个数据集在有无正则化的结果是：


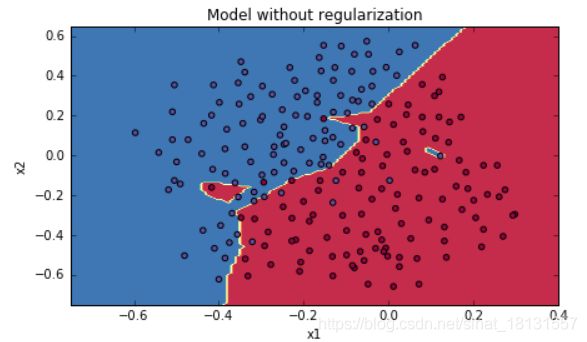
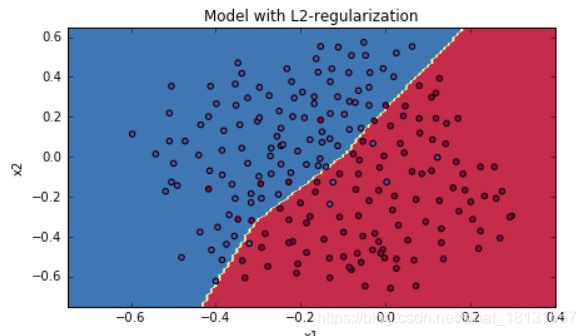
在逻辑回归中，正则化就是在损失函数添加一项：
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}l({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}_2^2$$或者$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}l({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}_1$$其中：

• L2正则化：$\frac{\lambda }{2m}||w|{|}_2^2=\frac{\lambda }{2m}\sum _{j=1}^{n_x}{w}_j^2=\frac{\lambda }{2m}{w}^{T}w$
• L1正则化：$\frac{\lambda }{2m}||w|{|}_1=\frac{\lambda }{2m}\sum _{j=1}^{n_x}|w_j|$

L2正则化使用较多。$\lambda$是一个正则化的超参数。
在神经网络中，加入正则化项的损失函数为： $$J(w^{[1]},b^{[1]},\cdots ,w^{[L]},b^{[L]})=\frac{1}{m}\sum _{i=1}^{m}l({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}\sum _{l=1}^L||w^{[l]}|{|}_F^2$$其中，$||w^{[l]}|{|}_2^2=||w^{[l]}|{|}_F^2=\sum _{i=1}^{n^{[l-1]}}\sum _{j=1}^{n^{[l]}}(w_{ij}^{[l]}{)}^2$，因为$w$是$n^{[l-1]}\times n^{[l]}$维的。
直观地来讲，当$J$不变时候，$\lambda$越大，有些$w^{[l],i}$就会变小，当$\lambda$足够大到某些$w^{[l],i}$约为零了，也就是这个节点消失（作用不强）了，就是简化了神经网络结构，所以可以减小过拟合的状态。
在编程实现中，由于$J$的前面一段就是之前计算的损失函数值，只需要在后面加上带有$\lambda$的项就可以了。$$J_{regularized}=\underset{\text{cross-entropy cost}}{-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\log \left(a^{[L](i)}\right)+(1-y^{(i)})\log \left(1-a^{[L](i)}\right))}+\underset{\text{L2 regularization cost}}{\frac{1}{m}\frac{\lambda }{2}\sum _l\sum _k\sum _j{W}_{k,j}^{[l]2}}$$
同时需要注意的是，由于$J$的表达式发生了变化所以$dW=\partial J/\partial W$也会发生变化，所以在反向传输的代码中也需要跟新为：$$d{W}^{[l]}=\text{(form\_backprop)}+\frac{\lambda }{m}{W}^{[l]}$$

Dropout

Dropout（随机失活）就是在神经网络的Dropout层，为每个神经元结点设置一个随机消除的概率，对于保留下来的神经元，我们得到一个节点较少，规模较小的网络进行训练。
假设对第3层神经网络进行dropout的python代码为：

keep_prob = 0.8  # 设置神经元保留概率
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
a3 = np.multiply(a3, d3)
a3 /= keep_prob

通过d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob语句得到一个与a3维度相同的举证，不过值是Bool量的true和false。这里解释下为什么要有最后一步：a3 /= keep_prob
依照例子中的keep_prob = 0.8 ，那么就有大约20%的神经元被删除了，也就是说$a^{[3]}$中有20%的元素被归零了，在下一层的计算中有$Z^{[4]}=W^{[4]}\cdot a^{[3]}+b^{[4]}$，所以为了不影响$Z^{[4]}$的期望值，所以需要$W^{[4]}\cdot a^{[3]}$的部分除以一个keep_prob。
Inverted dropout通过对“a3 /= keep_prob”,则保证无论keep_prob设置为多少，都不会对$Z^{[4]}$的期望值产生影响。
注意：在测试阶段不要用dropout，因为那样会使得预测结果变得随机。
另外一种对于Dropout的理解。
这里我们以单个神经元入手，单个神经元的工作就是接收输入，并产生一些有意义的输出，但是加入了Dropout以后，输入的特征都是有可能会被随机清除的，所以该神经元不会再特别依赖于任何一个输入特征，也就是说不会给任何一个输入设置太大的权重。
所以通过传播过程，dropout将产生和L2范数相同的收缩权重的效果。
对于不同的层，设置的keep_prob也不同，一般来说神经元较少的层，会设keep_prob
=1.0，神经元多的层，则会将keep_prob设置的较小²。
在tensorflow等深度学习框架中，通过设置参数keep_prob就可以直接设置dropout。不需要dropout就设置为1。

其他正则化方法

• 数据扩增：
  在图片识别等场合中，一辆车的朝向不重要（车头朝左，车头超右），都认为是车。车是不是在正中间不重要，都认为是车。所以可以直接将图片数据通过一定的平移旋转就可以得到“新的”样本数据。
• Early stopping：
  在交叉验证集的误差上升之前的点停止迭代，避免过拟合。这种方法的缺点是无法同时解决bias和variance之间的最优。
• 输入参数归一化
  比如输入参数有2个，$x_1,x_2$,其中，$x_1$范围为(0,1),$x_2$范围为(10,1000)，那么两个参数的权重将有很大不同，为了优化$x_1$的参数，学习率就要调低，但是就减慢了$x_2$的下降速度。其方法为参数去均值，归一化方差。$\mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)},x:=x-\mu ,{\sigma }^2=\frac{1}{m}\sum _{i=1}^m{x}^{(i{)}^2},x=x/{\sigma }^2$

梯度消失/梯度爆炸问题

首先假设有下图这样的一个网络，为了简化方程，假设$g(z)=z,b^{[l]}=0$,那么就有：$$\hat{y}=W^{[L]}{W}^{[L-1]}\cdots W^{[2]}{W}^{[1]}X$$

• 当$W^{[l]}$的值大于1时：
  比如$W^{[l]}=\left[\begin{array}{lc}1.5& 0\\ 0& 1.5\end{array}\right]$,那么，$\hat{y}=W^{[L]}{\left[\begin{array}{lc}1.5& 0\\ 0& 1.5\end{array}\right]}^{L-1}X$,激活函数的值将以指数方式递增。
• 当$W^{[l]}$的值小于1时：
  比如$W^{[l]}=\left[\begin{array}{lc}0.5& 0\\ 0& 0.5\end{array}\right]$,那么，$\hat{y}=W^{[L]}{\left[\begin{array}{lc}0.5& 0\\ 0& 0.5\end{array}\right]}^{L-1}X$,激活函数的值将以指数方
  式递减。

上面的情况对于导数也是同样的道理，所以在计算梯度时，根据情况的不同，梯度函数会以指数级递增或者递减，导致训练导数难度上升，梯度下降算法的步长会变得非常非常小，需要训练的时间将会非常长。
在梯度函数上出现的以指数级递增或者递减的情况就分别称为梯度爆炸或者梯度消失。
解决梯度消失或者梯度爆炸问题的方式就是进行合理的参数初始化，对于一个神经元来说，$z={\sum }_n^{i=1}{w}^{[i]}{x}^{[i]}$,当$n$比较大时候，只有$w^{[i]}$小，才能让z小。需要在随机参数的基础上乘以参数np.sqrt(1/n),也就是Xavier initialization，前面提到ReLU，使用He initialization也是比较好的。

	WL = np.random.randn(WL.shape[0],WL.shape[1])* np.sqrt(1/n)

梯度检查

对于导数的离散计算方法定义，是这样的：$$f^{\prime }(\theta )=\underset{\epsilon \to 0}{\lim }=\frac{f(\theta +\epsilon )-(\theta )}{\epsilon }$$还有一种双边导数$$f^{\prime }(\theta )=\underset{\epsilon \to 0}{\lim }=\frac{f(\theta +\epsilon )-(\theta -\epsilon )}{2\epsilon }$$他们的误差分别为$O({\epsilon }^2),O(\epsilon )$
在离散计算中，不能得到导数的精确值，只有无限逼近精确值，显然双边导数的计算方式更加接近精确值。使用$d{\theta }_{approx}$表示双边计算导数，使用$d\theta$表示单边计算导数，那么$$diffrence=\frac{||d{\theta }_{approx}-d\theta |{|}_2}{||d{\theta }_{approx}|{|}_2+||d\theta |{|}_2}$$其中，$||\cdot |{|}_2$表示欧几里得范数，在python代码中使用np.linalg.norm()表示。设置$\epsilon =10^{-7}$,diffrence小于$\epsilon$或者相当时候，证明梯度表达式没有问题，当$\epsilon$比较大，约为$10^{-5}$时候，表示可能有问题，当$\epsilon$明显很大时，就要认真检查梯度的表达式是不是有错误了。
由于损失函数中的参数非常多$W^{[l]}$和$b^{[l]}$,要对所有的参数进行梯度检查的话，就需要把所有的参数转化为一个很大的向量。为$J({\theta }_1,{\theta }_2,...)$，$\theta$向量的长度可以表示为$L_{\theta }={\sum }_{i=1}^L(W^{[i]}.shape[0]\times W^{[i]}.shape[1]+len(b^{[i]}))$，实现的伪代码为：

for i in range(len(theta)):
	thetaplus[i] = thetaplus[i]+epsilon
	thetaminus[i] = thetaminus[i]-epsilon
	J_plus[i] = forward_propagation_n(X, Y, thetaplus)
	J_minus[i] = forward_propagation_n(X, Y, thetaminus)
	gradapprox[i] = (J_plus[i]-J_minus[i])/(2*epsilon)
difference = np.linalg.norm(grad-gradapprox)/(np.linalg.norm(grad)+np.linalg.norm(gradapprox))

注意：梯度检查是耗时的操作，只有在需要进行的时候才进行梯度检查，正常训练时候不需要。

代码实现

2.1.第一周 深度学习的实用层面

算法优化

mini-batch梯度下降

使用一个样本的训练速度很慢，并且下降梯度并不是都是沿着下降的方向进行，只是大体上是下降的趋势，然而使用整个数据集去训练在遇到很大的数据集时候，计算机配置问题也可能很慢，甚至由于计算机的CPU/GPU内存不够直接导数无法训练。所以就有了mini-batch的梯度下降，其实就是把整个训练集分成了多个批，每次送入一批数据样本进去训练，这样的性能实际上是在随机梯度下降(Stochastic Gradient Descent)（一个一个样本训练）和整体梯度下降(Batch Gradient Descent) 法（整个训练集送入）中间，但是在数据量大时候，这个方式非常好。一般的batch_size取（64，128，256，512）等值，当然也看网络复杂程度与计算机配置（内存与显存）。
对比随机梯度下降和梯度下降方法，明显随机梯度下降的噪声比较大：

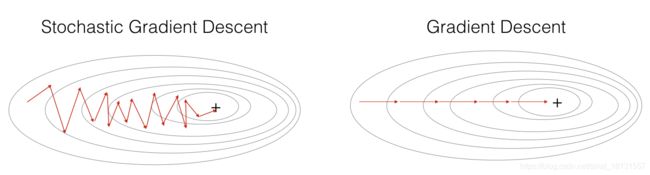
而mini-batch梯度下降介于两者之间：

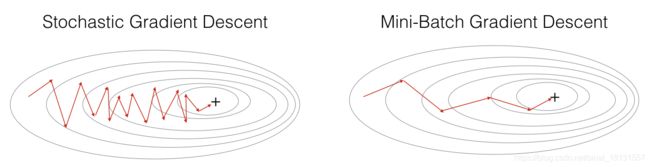
数学记号：当左所有数据进行训练时，使用的样本标记为$\{X,Y\}$表示样本的输入参数与真实标签，在mini-batch梯度下降方式中使用$\{X^{\{i\}},Y^{\{i\}}\}$表示第$i$批样本。
另外一个概念epoch就是使用mini-batch梯度下降遍历了整个数据集一次。

指数加权平均

指数加权平均是用于理解Momentum算法的，由于一个样本训练后更新了$W,b$后，后面还有很多很多的样本去训练参数，也就是说如果训练了10000次之后，第1次训练的权重就很少了。有的时候，我们还是希望之前的部分参数信息可以保留到后面的结果中。再如，由于使用随机梯度下降或者mini-batch梯度下降的时候，损失函数是有噪声地下降，这时候，如果对之前的损失函数值做个记录，在当前次的下降过程中，任考虑了之前的下降方向，那么损失函数将会光滑一些。其方式为：$$V_t=\beta V_{t-1}+(1-\beta ){\theta }_t$$$V_{t-1}$表示前一次的下降方向，${\theta }_t$表示当前的计算方向，通过不断递归$V_t=\beta (\beta V_{t-2}+(1-\beta ){\theta }_{t-1})+(1-\beta ){\theta }_t={\beta }^k{V}_{t-k}+{\sum }_{i=1}^k(1-\beta {)}^i{\theta }_{t-i+1}$，可以看出当前次的下降方向与之前都有一定程度的关系，但是关系不是线性的，有权重。$\beta$是这里的一个超参数，在数学中$(1-\epsilon {)}^{(1/\epsilon )}\approx \frac{1}{e}\approx 0.35$,当$\beta =0.9$时，相当于在前面10次的权重大于0.33左右，在之前的就比较小了。
在编程中实现可以不要这么多变量，只要$v_{\theta }$就好了。$$v_{\theta }:=\beta v_{\theta }+(1-\beta ){\theta }_t$$
但是在这样的方法中，在最初的迭代中，比如第一次和第二次（$\beta =0.9$），初始化$V_0=0$，$V_1=0.1{\theta }_1,V_2=0.9V_1+0.1{\theta }_2=0.09{\theta }_1+0.1{\theta }_2$,导致了前面几个迭代中偏差很大，所以需要进行偏差修正$$\begin{gathered} v_{\theta }:=\beta v_{\theta }+(1-\beta ){\theta }_t \\ {v}_{\theta }:=\frac{v_{\theta }}{1-{\beta }^t} \end{gathered}$$当$t$较小时候，$1-{\beta }^t$的值也比较小，就可以得到一个正常的值。由于在深度学习中，迭代次数总是大量的，所以在开始阶段的一些偏差问题可以问题不大，所以不一定都有偏差修正的过程。

动量梯度下降法(Momentum)

将指数加权平均的方法应用到梯度下降的过程中就是动量梯度下降法。在梯度下降方法中，使用$W:=W-\alpha dW$和$b:=b-\alpha db$的方式更新参数。同样，希望保留参数之前训练的方向，那么$$\begin{gathered} v_{dW}=\beta v_{dW}+(1-\beta )dW \\ {v}_{db}=\beta v_{db}+(1-\beta )db \\ W:=W-\alpha v_{dW} \\ b:=b-\alpha v_{db} \end{gathered}$$参数$\beta$的常用范围是0.8~0.999，一般缺省为0.9没什么大问题。

RMSprop(root mean square prop)

在动量梯度下降法中进一步思考，由于各个参数的数量值大小不一样的，是否可以将他们按照某种方式归一化操作呢，在数值区间小的方向变化慢一些，在数值区间大的方向变化快一些？（自己的理解，可能不正确），于是有了与动量梯度下降法类似的处理方法优化下降过程：$$\begin{gathered} s_{dW}=\beta s_{dW}+(1-\beta )d{W}^2 \\ {s}_{db}=\beta s_{db}+(1-\beta )d{b}^2 \\ W:=W-\alpha \frac{dW}{\sqrt{s_{dW}}} \\ b:=b-\alpha \frac{db}{\sqrt{s_{db}}} \end{gathered}$$为了防止分母为0或者接近于0导致计算出现nan问题，部分会在分布上添加一个较小的偏置项。即为：$$\begin{gathered} s_{dW}=\beta s_{dW}+(1-\beta )d{W}^2 \\ {s}_{db}=\beta s_{db}+(1-\beta )d{b}^2 \\ W:=W-\alpha \frac{dW}{\sqrt{s_{dW}}+\epsilon } \\ b:=b-\alpha \frac{db}{\sqrt{s_{db}}+\epsilon } \end{gathered}$$

Adam(Adaptive Moment Estimation)

还有一个常用的优化方式就是Momentum与RMSprop结合的方式，$$\{\begin{array}{l}{v}_{d{W}^{[l]}}={\beta }_1{v}_{d{W}^{[l]}}+(1-{\beta }_1)\frac{\partial \mathcal{J}}{\partial W^{[l]}}\\ v_{d{W}^{[l]}}^{corrected}=\frac{v_{d{W}^{[l]}}}{1-({\beta }_1{)}^t}\\ s_{d{W}^{[l]}}={\beta }_2{s}_{d{W}^{[l]}}+(1-{\beta }_2)(\frac{\partial \mathcal{J}}{\partial W^{[l]}}{)}^2\\ s_{d{W}^{[l]}}^{corrected}=\frac{s_{d{W}^{[l]}}}{1-({\beta }_1{)}^t}\\ W^{[l]}=W^{[l]}-\alpha \frac{v_{d{W}^{[l]}}^{corrected}}{\sqrt{s_{d{W}^{[l]}}^{corrected}}+\epsilon }\end{array}$$这是参数$W$的更新方式，参数$b$的更新方式一样的。
推荐的参数${\beta }_1=0.9,{\beta }_2=0.999,\epsilon =10^{-8}$，Adam算法的论文参考：ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
在代码实现中，发现明显Adam算法的准确率要高。

optimization method	accuracy	cost shape
Gradient descent	79.7%	oscillations
Momentum	79.7%	oscillations
Adam	94%	smoother

学习率衰减

在刚开始训练时候，希望非常迅速地下降到最优值附近，所以这是个学习率大一些好，但是在快到最优值附近时候，如果学习率还是很大，就会在最优值附近震荡，不会收敛于最小值。所以整个训练过程，学习率也在减小的话也能优化模型。
衰减方法：

• 常用 $$\alpha =\frac{1}{1+decay\_rate\ast epoch\_num}{\alpha }_0$$
• 指数衰减$$\alpha =0.95^{epoch\_num}{\alpha }_0$$
• 其他$$\alpha =\frac{k}{epoch\_num}\cdot {\alpha }_0$$
• 离散下降，不同阶段使用不同学习率，通过条件设计

关于局部最优值问题

在一个具有高维度空间的函数中，如果梯度为0，那么在每个方向，Cost function可能是凸函数，也有可能是凹函数。但如果参数维度为2万维，想要得到局部最优解，那么所有维度均需要是凹函数，其概率为$2^{-20000}$，可能性非常的小。也就是说，在低纬度中的局部最优点的情况，并不适用于高纬度，我们在梯度为0的点更有可能是鞍点。在深度学习中不考虑局部最优问题。
在高纬度的情况下：

• 几乎不可能陷入局部最小值点；
• 处于鞍点的停滞区会减缓学习过程，利用如Adam等算法进行改善。

代码实现

2.2.第二周 优化算法

超参数调试、Batch正则化和程序框架

关于超参数

在神经网络中，通常的超参数有学习率$\alpha$,神经网络的层数$L$,每层的节点数$n^{[l]}$,学习率下降方式与系数，batch size,Momentum中的$\beta$,Adam中的${\beta }_1,{\beta }_2,\epsilon$等。通常来讲，学习率$\alpha$是最重要的，应该是优先调整的，合适的学习率能让模型的性能大大提升。然后重要的是网络的层数$L$和学习率下降，再然后$n^{[l]},batch\_size,\beta \text{(in Momentum)}$，对于Adam的参数Andrew建议为${\beta }_1=0.9,{\beta }_2=0.999,\epsilon =10^{-8}$。使用的调试方法就是首先随机找一些值，看在哪个范围内比较好，然后再这个小范围内继续找合适的不断优化。比如，学习率的初始范围为0.0001-0.1,随机找发现在0.001-0.01中比较合适，再继续再这个范围内找最优的。但是把0.0001-0.1画在数轴上会发现，随机落在0.0001-0.001的概率是0.9%，然而我们希望落在0.0001-0.001,0.001-0.01,0.01-0.1这几个范围内的概率是相等的，就需要取对数方式实现。如实现0.0001-0.1范围内的随机的话，r=-3*np.random.rand()-1，这样$r\in [-4,-1]$,然后alpha = np.power(10,r),这样$\alpha \in [0.0001,0.1]$并且我们希望的随机性更好。

Batch正则化(Batch Normalization)

在上文中的其他正则化方法中的输入参数归一化中，把逻辑回归的输入参数做了归一化有助于提高模型性能与下降速度$$\begin{gathered} \mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)} \\ {\sigma }^2=\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu {)}^2 \\ x=\frac{x-\mu }{{\sigma }^2} \end{gathered}$$是否可以将每层的输入都做归一化？YES!
对于$l+1$层的输入为$a^{[l]}$,实际上归一化的参数为$z^{[l]}$,那么$z^{[l]}=\{z^{[l](1)},z^{[l](2)},...,z^{[l](m)}\}$有：$$\begin{gathered} \mu =\frac{1}{m}\sum _{i=1}^m{z}^{[l](i)} \\ {\sigma }^2=\frac{1}{m}\sum _{i=1}^m(z^{[l](i)}-\mu {)}^2 \\ {z}_{norm}^{[l](i)}=\frac{z^{[l](i)}-\mu }{\sqrt{{\sigma }^2+\epsilon }} \end{gathered}$$这样$z_{norm}^{[l]}$就是均值为0，方差为1的标准分布，但是有的时候，分布状态可能还是有信息的，使用参数来输出$$z^{(i)}=\gamma z_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}^{[l]}+\beta$$这里的$\gamma$和$\beta$是可以学习更新的参数，就像之前的$w$和$b$一样，他们决定了正则化参数的分布状态。
有了Batch Norm的计算流程图为：

w1,b1

gamma1,beta1

g

w2,b2

X

Z1

Z_norm1

a1

Z2

...

这里需要学习的参数就有$\{w^{[1]},b^{[1]},{\gamma }^{[1]},{\beta }^{[1]},...,w^{[L]},b^{[L]},{\gamma }^{[L]},{\beta }^{[L]}\}$,梯度下降中就需要更新参数：$$\begin{gathered} W^{[l]}=W^{[l]}-\alpha d{W}^{[l]} \\ {b}^{[l]}=b^{[l]}-\alpha d{b}^{[l]} \\ {\beta }^{[l]}={\beta }^{[l]}-\alpha d{\beta }^{[l]} \\ {\gamma }^{[l]}={\gamma }^{[l]}-\alpha d{\gamma }^{[l]} \end{gathered}$$使用Momentum，RMSprop,或者Adam优化时候，添加上特有项即可。Batch Norm在tensorflow中实现可以直接使用tf.nn.batch_normalization()完成。
由于去均值的过程就是把偏置去掉，而$Z=Wx+b$中的偏置项就是参数$b$，所以在实际训练中，其实可以不用管$b$,训练好$W,\gamma ,\beta$三个参数就好了。

为什么batch Norm有效

假设有一个模型是猫/非猫的0-1判断的，然后训练样本的猫全是黑色的，而这样训练出来的模型，就不能很好地识别其他颜色的猫，但是，去除了图片的均值，这样能把一定的细节加以强化，这样就能识别不是黑色的猫了。Batch Norm的作用便是其限制了前层的参数更新导致对后面网络数值分布程度的影响，使得输入后层的数值变得更加稳定。另一个角度就是可以看作，Batch Norm 削弱了前层参数与后层参数之间的联系，使得网络的每层都可以自己进行学习，相对其他层有一定的独立性，这会有助于加速整个网络的学习。
在使用Mini-batch梯度下降的时候，每次计算均值和偏差都是在一个Mini-batch上进行计算，而不是在整个数据样集上。这样就在均值和偏差上带来一些比较小的噪声。那么用均值和偏差计算得到的$z^{[l]}$也将会加入一定的噪声。所以和Dropout相似，其在每个隐藏层的激活值上加入了一些噪声，（这里因为Dropout以一定的概率给神经元乘上0或者1）。所以和Dropout相似，Batch Norm 也有轻微的正则化效果。这里引入一个小的细节就是，如果使用Batch Norm ，那么使用大的Mini-batch如256，相比使用小的Mini-batch如64，会引入跟少的噪声，那么就会减少正则化的效果。

测试集上的Batch Norm问题

在训练时候，由于每次送入训练的数据量为$batch\_size$大小，可以有去平均与方差的操作，但是在测试数据时候，有时候仅仅使用的是一个样本去做测试或者预测。这时候就没有平均与方差的概念了。所以在训练时候需要对平均$\mu$和方差${\sigma }^2$进行估计。对于训练集的Mini-batch，使用指数加权平均，当训练结束的时候，得到指数加权平均后的均值$\mu$和方差${\sigma }^2$,比方说第一个batch会计算出均值${\mu }_1$和方差${\sigma }_1^2$,第二个batch会计算出均值${\mu }_2$和方差${\sigma }_2^2$…这样就能使用指数加权平均来估计一个均值${\mu }_{avg}$和方差${\sigma }_{avg}^2$。

神经网络的多分类问题

在输出层使用tanh或者sigmoid等激活函数能解决二分类的问题。但是在实际中还有多分类的问题，多分类问题在输出层中就有多个神经元，而非一个。如四分类时候，最后一层的输出就是$4\times 1$维的，在最后一层还想知道计算到这一层的概率。就可以使用softmax函数实现，softmax的输入假设为$\{x_1,x_2,x_3,x_4\}$,那么输出：$$s_j=\frac{e^{x_j}}{\sum _{i=1}^4{e}^{x_i}},j\in [1,2,3,4]$$也就是说：$$\begin{gathered} s_1=\frac{e^{x_1}}{e^{x_1}+e^{x_2}+e^{x_3}+e^{x_3}} \\ ...... \\ {s}_4=\frac{e^{x_4}}{e^{x_1}+e^{x_2}+e^{x_3}+e^{x_3}} \end{gathered}$$这里我们能得到$\sum _{i=1}^4{s}_i=1$就表达了计算每个类别的概率，那么概率最大的那个就认为了计算的类别了。
使用softmax的损失函数定义为：$$L(a,y)=-\sum _{i=1}^C{y}_i\text{log}{a}_i$$,对于真实标签，认为是当前类别的该位为1，其余为0，如输出4类，他是第二类时候，真实标签表示为：$y=[0,1,0,0{]}^T$(列向量)。即$y_1=y_3=y_4=0,y_2=1$，$$L(a,y)=-\sum _{i=1}^C{y}_i\text{log}{a}_i=-y_2\text{log}{a}_2=-\text{log}{a}_2$$优化的目标是$a_2$尽可能大，也就是$L$尽可能小。一次送入$m$个样本时候的损失函数表示为：$$J(w^{[1]},b^{[1]},\dots )=\frac{1}{m}\sum _{i=1}^{m}L(a^{(i)},y^{(i)})$$使用链式求导法则可以进一步计算使用softmax进行反向传播的公式表示为：$$\frac{\partial J}{\partial z^{[L]}}=d{z}^{[L]}=a-y$$

深度学习框架

在实际使用中，通常不会去自己从零开始写神经网络，现在有比较成熟的深度学习框架，使用比较简单，甚至可以半小时搭建一个神经网络起来。但是，Andrew的课程从最基础开始逐步加深理解，是对基础知识的很好梳理。应该先把Andrew的课程看完了，能自己搭建网络了再使用框架，理解就非常透彻了。常用的框架有tensorflow(Google),CNTK(Microsoft),DL4J(Eclipse for Java), Keras,mxnet(Apache),PaddlePaddle(百度)，caffe/caffe(Berkley)。
使用tensorflow的一段代码示例：

# 导入使用的库
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

# 参数
coefficients = np.array([[1.], [-10.], [25.]])
# 创建需要优化的变量
w = tf.Variable([0], dtype=tf.float32)
# placeholder用于放数据
x = tf.placeholder(tf.float32, [3, 1])
# 损失函数的定义式
cost = x[0][0] * w ** 2 + x[1][0] * w + x[2][0]
# 使用梯度下降法优化，学习率为0.01，优化目标是最小化cost
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
# 参数初始化
init = tf.global_variables_initializer()
# 创建会话，并运行参数初始化
session = tf.Session()
session.run(init)
costs = []
for i in range(1000):
    # 训练，使用coefficients代替x
    session.run(train, feed_dict={x: coefficients})
    # 将数据cost历史数据保存
    costs.append(session.run(cost, feed_dict={x: coefficients}))
    if not i % 100:
        print(session.run(w, feed_dict={x: coefficients}), '\t->', session.run(cost, feed_dict={x: coefficients}))
# cost轨迹绘图
plt.plot(costs)
plt.show()

---

1. 网易公开课，神经网络和深度学习，https://mooc.study.163.com/smartSpec/detail/1001319001.htm ↩︎

2. 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（2-1）-- 深度学习的实践方面, https://blog.csdn.net/Koala_Tree/article/details/78125697 ↩︎