《机器学习》周志华 第二章——模型评估与选择笔记

《机器学习》周志华 第二章——模型评估与选择

过拟合和欠拟合

过拟合：对训练数据拟合过当的情况，训练集表现很好，测试集表现差。

欠拟合：模型在训练和预测时都表现不好。

降低过拟合的方法：

1、获得更多的训练数据，让模型学习更多有效的特征，减少噪声的影响。但直接增加实验数据比较难，可以通过规则扩充数据，比如对不平衡样本做SMOTE采样，在图像分类中对原始图像进行平移、旋转、缩放等方式填充数据；通过生成式对抗网络合成新的训练数据。

2、降低模型复杂度，模型过于复杂是产生过拟合的主要因素，神经网络模型中减少层数，神经元个数，树模型中剪枝和减少深度。

3、正则化方法，为参数的引入增加一定的惩罚。以L2正则为例：

$$C=C_0+\frac{\lambda }{2n}\Sigma w_i^2$$

4、集成学习方法，将多个模型集成在一起，降低单模型的过拟合风险。如Bagging

降低欠拟合的方法：

1、增加新特征。特征不足的时候容易出现欠拟合，很多模型可以完成辅助特征工程，GPlearn、Geepy、演化森林等遗传规划框架、OpenFE、因子分解机、梯度提升决策树、Deep-crossing等。

2、增加模型复杂度，线性模型加高次项、网络加层、树加深度。

3、减小正则化的惩罚系数

评估方法

留出法：划分中尽量保证训练集和测试集的样本分布一致性。可以通过分层采样方法得到。单次留出法不稳定，可以进行多次。常见做法将$2/3-4/5$的样本作为训练集。

交叉验证法：k-fold交叉验证，样本划分成k个大小相等的子集，遍历子集，当前子集为测试集，其余为训练集，进行模型训练和评估。把k次评估指标的平均值作为最终的评估指标。实际中k往往取5、10

留一验证：留下来1个样本作为测试集，样本容量为$n$的数据，要构建$n$次模型计算开销大。

自助法：Boostrap法，对总数为$n$的样本进行$n$次有放回随机抽样，得到样本容量为$n$的训练集，$n$采样中有些样本被重复采样，有些样本没有被采样，未抽出的作为验证集，这就是自助法的过程。没有抽到的这部分叫做袋外观侧（包外）Out-of-bag-estimate.自助法在数据集较小、难以有效划分训练/测试集时很有用;此外,自助法能从初始数据集中产生多个不同的训练集,这对集成学习等方法有很大的好处。但改变了数据分布情况，在初始数据量足够时,留出法和交叉验证法更常用一些。

自助法对总数为$n$的样本进行$n$次有放回随机抽样，得到样本容量为$n$的训练集，有多少样本最终没有被选择过？
$$\underset{n\to +\infty }{\lim }{\left(1-\frac{1}{n}\right)}^n=\frac{1}{e}=0.367879$$
当样本量很大的时候，36.8%的样本没有被选择过。

调参方法

超参数搜索算法一般具有几个要素，最大化最小化的目标、搜索范围（上下限）、算法其他参数（搜索步长）

有哪些搜索方法?

1、网格搜索：查找范围内所有点来确定最优值，如果采用较大的搜索范围和较小的步长有可能得到全局最优解。但代价是异常高的计算资源。应用中往往通过大范围和大步长先缩小搜索范围，然后在小范围中小步长搜索最优解。但可能不一定最优。

2、随机搜索：不再测试上下界之间的所有值，在范围中随机选取样本点，如果样本点抽取足够多也是有大概率得到全局最优的，一般比网格搜索更快，但同样结果不一定是全局最优。

3、贝叶斯优化：对目标函数的形状进行学习，找到使得目标函数向全局最优提升的参数，每一次用新的采样点测试目标函数时候，利用信息来更新目标函数的先验分布，但贝叶斯算法容易陷入局部最优，在局部反复采样。弥补这个缺陷会在未采样地区和最可能出现全局最优的局部地区都进行采样，得到“平衡”。

4、智能算法进行参数优化——遗传算法的例子：

1. 产生初始种群：根据种群规模，随机产生初始种群，每个个体表示染色体的基因型，即机器学习模型的参数组合。

2. 计算适应度：计算每个个体的适应度，即目标函数的值，如机器学习模型的准确率或损失函数。判断是否满足优化准则，若满足，则输出最佳个体及其代表的最优解，并结束算法；若不满足，则转入下一步。

3. 选择：依据适应度选择再生个体，适应度高的个体被选中的概率高，反之，适应度低的个体被选中的概率低，甚至可能被淘汰。

4. 交叉：根据一定的交叉概率和交叉方法生成子代个体，即通过染色体的交换产生新的参数组合。

5. 变异：根据一定的变异概率和变异方法，生成子代个体，即通过染色体的改变产生新的参数组合。

6. 重复步骤2-5，直到达到预设的进化代数或满足优化准则。

性能度量

回归任务——均方误差：
$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

$$E(f;\mathcal{D})={\int }_{\mathbf{x}\sim \mathcal{D}}(f(\mathbf{x})-y{)}^{2}p(\mathbf{x})\mathrm{d}\mathbf{x}$$

分类任务——错误率

$E(f;D)=\frac{1}{m}{\sum }_{i=1}^m\mathbb{I}\left(f\left({\mathbf{x}}_i\right)\ne y_i\right)$

精度

$\begin{array}{rl}\mathrm{acc}(f;D)& =\frac{1}{m}\sum _{i=1}^m\mathbb{I}\left(f\left({\mathbf{x}}_i\right)=y_i\right)\\ & =1-E(f;D)\end{array}$

一般的在已知分布D和概率密度p(·)的情况下错误率和精度可以描述为：

$E(f;\mathcal{D})={\int }_{\mathbf{x}\sim \mathcal{D}}\mathbb{I}(f(\mathbf{x})\ne y)p(\mathbf{x})\mathrm{d}\mathbf{x}$

$\begin{array}{rl}\mathrm{acc}(f;\mathcal{D})& ={\int }_{\mathbf{x}\sim \mathcal{D}}\mathbb{I}(f(\mathbf{x})=y)p(\mathbf{x})\mathrm{d}\mathbf{x}\\ & =1-E(f;\mathcal{D}).\end{array}$

查准率(precision)、查全率(recall)

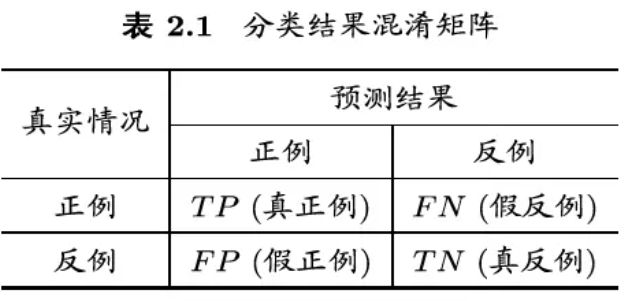$$ \begin{aligned} P & =\frac{T P}{T P+F P} \\ R & =\frac{T P}{T P+F N}\end{aligned} $$ 查准率和查全率是一对矛盾的度量.一般来说,查准率高时,查全率往往偏低;而查全率高时,查准率往往偏低.

我们可根据学习器的预测结果对样例进行排序,排在前面的是学习器认为“最可能”是正例的样本,排在最后的则是学习器认为“最不可能”是正例的样本.按此顺序逐个把样本作为正例进行预测,即可计算出计算出当前的查全率、查准率.

若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者,例如图2.3中学习器A的性能优于学习器C。

F1值（本质是查准率和查全率的调和平均）
$$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{\text{样例总数}+TP-TN}$$
$F_{\beta }$是查准率和查全率的加权调和平均，可以根据问题对查准率和查全率的不同要求来调整$\beta$。
$$F_{\beta }=\frac{\left(1+{\beta }^2\right)\times P\times R}{\left({\beta }^2\times P\right)+R}$$
$\beta >1$查全率更重要，$\beta <1$查准率更重要。

ROC和AUC

ROC全称是“受试者工作特征”曲线,相似,我们根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算出两个重要量的值,分别以它们为横、纵坐标作图,就得到了“ROC曲线”与P-R曲线使用查准率、查全率为纵、横轴不同,ROC曲线的纵轴是“真正例率”,简称FPR.横轴是“假正例率”FPR

$\begin{array}{rl}\mathrm{TPR}& =\frac{TP}{TP+FN}\\ \mathrm{FPR}& =\frac{FP}{TN+FP}\end{array}$

AUC为ROC曲线下的面积，估算为：

$\mathrm{AUC}=\frac{1}{2}{\sum }_{i=1}^{m-1}\left(x_{i+1}-x_i\right)\cdot \left(y_i+y_{i+1}\right)$