机器学习实战-梯度下降法在线性回归模型中的使用

数据集简介

  使用的数据集是波士顿房价，具体在：机器学习实战-波士顿房价及能源效能数据的相关分析的线性回归模型

线性回归

线性回归首先假设自变量和因变量是线性关系，然后通过对现有
样本进行回归，进而计算出回归系数以确定线性模型，最后使用这
个模型对未知样本进行预测

• 一元线性回归模型：$f(x)=wx+b$
• 多元线性回归模型：$f(x)=w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n+b$

线性回归的衡量指标

1. MSE(Mean Squared Error):均方误差
   
2. RMSE(Root Mean Squared Error):均方根误差
   
3. MAE(Mean Absolute Error):平均绝对误差
   
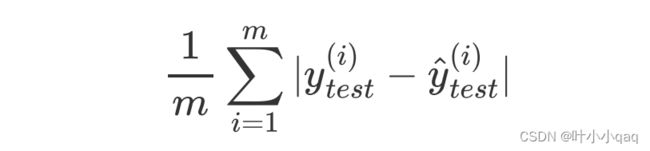
4. R方指标(R Squared)
   

• $R^2<=1$
• $R^2$越大越好。当预测模型没有任何错误时,$R^2$等于1
• 引入$R^2$衡量指标的原因：可以对不同回归问题的模型准确度
  进行统一衡量(例如：房价线性回归问题和学生成绩线性回归
  问题)

载入数据集

from sklearn import datasets

boston = datasets.load_boston()  # 波士顿房子数据集
X = boston.data   # 样本特征
y = boston.target  # 样本标签
X = X[y<50]
y = y[y<50]

拆分数据集

# 拆分数据集
from sklearn.model_selection import train_test_split

X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=666)

标准化样本特征

# 标准化样本特征
from sklearn.preprocessing import StandardScaler

std = StandardScaler()
std.fit(X_train)
X_train_std = std.transform(X_train)
X_test_std = std.transform(X_test)

计算损失函数值

# 计算损失函数值
def J(X_b,y,theta):
    try:
        return np.sum((X_b.dot(theta) - y) ** 2) / 2 * len(y)
    except:
        return float('inf')

梯度下降法的介绍请看：梯度下降算法实现原理(Gradient Descent)

计算梯度

# 计算梯度（针对一组theta参数的偏导数）
def dJ(X_b,y,theta):
    return X_b.T.dot(X_b.dot(theta) - y) / len(y)

以批量梯度下降法为例

# 以批量梯度下降法为例
def BGD(X_b,y,initial_theta,eta=0.01,iters=1e4,epsilon=1e-4):
    theta = initial_theta   # 将参数的初始值赋给theta变量
    curr_iter = 1
    while curr_iter < iters:   # 判断迭代次数
        gradient = dJ(X_b,y,theta)  # 计算当前theta对应的梯度
        last_theta = theta  # 先保存theta的旧值
        theta = theta - eta * gradient  # 更新theta
        cost_value = J(X_b,y,theta)  # 计算更新后的theta对应的损失函数值
        last_cost_value = J(X_b,y,last_theta)  # 计算更新前的theta对应的损失函数值
        # 如果两次损失函数的值相差的非常小，则认为损失函数已经最小了
        if abs(cost_value - last_cost_value) < epsilon:
            break
        curr_iter += 1  # 每次迭代完毕，迭代次数加1
    return theta,cost_value   # 返回最佳的theta和对应的损失函数值

# 拼接训练样本的X_b
X_b = np.hstack([np.ones((len(X_train_std),1)),X_train_std])
# 初始化theta
initial_theta = np.random.random(size=(X_b.shape[1]))

theta,cost_value = BGD(X_b,y_train,initial_theta,iters=1e5)
print("搜索的最佳参数是：",theta)

测试集预测

# 拼接测试样本的X_b
X_b_test = np.hstack([np.ones((len(X_test_std),1)),X_test_std])
# 在测试集上预测
y_predict = X_b_test.dot(theta)

from sklearn.metrics import mean_squared_error

r2 = 1 - mean_squared_error(y_test,y_predict) / np.var(y_test)
print("在测试集上的R方为：",r2)

scikit-learn使用SGD实现

from sklearn.linear_model import SGDRegressor

# 创建对象，该对象可以使用SGD搜索线性回归中的最佳参数
sgd = SGDRegressor()  
sgd.fit(X_train_std,y_train)  # 在训练集上进行拟合
r2 = sgd.score(X_test_std,y_test)  # 在测试集上计算R方指标
print("在测试集上的R2指标为：",r2)

全部代码

import numpy as np
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error


boston = datasets.load_boston()  # 波士顿房子数据集
X = boston.data   # 样本特征
y = boston.target  # 样本标签
X = X[y<50]
y = y[y<50]

# 拆分数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=666)

# 标准化样本特征
std = StandardScaler()
std.fit(X_train)
X_train_std = std.transform(X_train)
X_test_std = std.transform(X_test)

# 计算损失函数值
def J(X_b,y,theta):
    try:
        return np.sum((X_b.dot(theta) - y) ** 2) / 2 * len(y)
    except:
        return float('inf')

# 计算梯度（针对一组theta参数的偏导数）
def dJ(X_b,y,theta):
    return X_b.T.dot(X_b.dot(theta) - y) / len(y)

# 以批量梯度下降法为例
def BGD(X_b,y,initial_theta,eta=0.01,iters=1e4,epsilon=1e-4):
    theta = initial_theta   # 将参数的初始值赋给theta变量
    curr_iter = 1
    while curr_iter < iters:   # 判断迭代次数
        gradient = dJ(X_b,y,theta)  # 计算当前theta对应的梯度
        last_theta = theta  # 先保存theta的旧值
        theta = theta - eta * gradient  # 更新theta
        cost_value = J(X_b,y,theta)  # 计算更新后的theta对应的损失函数值
        last_cost_value = J(X_b,y,last_theta)  # 计算更新前的theta对应的损失函数值
        # 如果两次损失函数的值相差的非常小，则认为损失函数已经最小了
        if abs(cost_value - last_cost_value) < epsilon:
            break
        curr_iter += 1  # 每次迭代完毕，迭代次数加1
    return theta,cost_value   # 返回最佳的theta和对应的损失函数值

# 拼接训练样本的X_b
X_b = np.hstack([np.ones((len(X_train_std),1)),X_train_std])
# 初始化theta
initial_theta = np.random.random(size=(X_b.shape[1]))

theta,cost_value = BGD(X_b,y_train,initial_theta,iters=1e5)
print("搜索的最佳参数是：",theta)

# 拼接测试样本的X_b
X_b_test = np.hstack([np.ones((len(X_test_std),1)),X_test_std])
# 在测试集上预测
y_predict = X_b_test.dot(theta)

r2 = 1 - mean_squared_error(y_test,y_predict) / np.var(y_test)
print("在测试集上的R方为：",r2)

博客园：https://www.cnblogs.com/yj179101536/