2023美国大学生数学建模竞赛C题思路解析（含代码+数据可视化）

以下为2023美国大学生数学建模竞赛C题思路解析（含代码+数据可视化）

规则：

猜词，字母猜对，位置不对为黄色，位置对为绿色，两者皆不对为灰色。

困难模式下的要求：对于猜对的字母（绿色和灰色），下一步必须使用

要求：

报告结果的数量每天都在变化。开发一个模型来解释这种变化，并使用您的模型为2023年3月1日报告的结果数量创建一个预测区间。单词的任何属性是否会影响在硬模式下播放的报告分数百分比？如果是，怎么办？如果没有，为什么不呢？

对于给定的未来解决方案单词，在未来的日期，开发一个模型，使您能够预测报告结果的分布。换句话说，预测未来日期（1，2，3，4，5，6，X）的相关百分比。你的模型和预测有哪些不确定性？举一个具体的例子，说明你对2023年3月1日EERIE一词的预测。你对模型的预测有多自信？

开发并总结一个模型，根据难度对解决方案单词进行分类。识别与每个分类相关的给定单词的属性。使用你的模型，EERIE这个词有多难？讨论分类模型的准确性。

列出并描述此数据集的一些其他有趣的功能。

最后，在给《纽约时报》拼图编辑的一到两页信中总结你的结果。

结果每天都在变化的原因：

是否工作日，人们尝试的意愿有多大

新增一列为是否为工作日，或者判断为周几

昨天或者前几天的难度对于游玩心态的影响

虽然尝试次数这里使用的是百分比，但是总分数与困难模式下的分数为具体的值，尝试的人的数量不同则总分不同。

单词的难度，包括长度，重复字母的数量，词性等 长度是固定的不需要考虑

存在的问题：对于同一个字母的多次使用，他是怎么进行显示的，比如我输入了全是A的情况，他显示的是除了对的位置是绿色，其他全是黄色还是其他的什么情况？

单词是否为常见词，或者和常见词的相似度

在此基础上就需要常见词库，以及单词相似度度量

需要预测的东西： 不同尝试次数的百分比分布，分数区间，困难的分数

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime

plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题


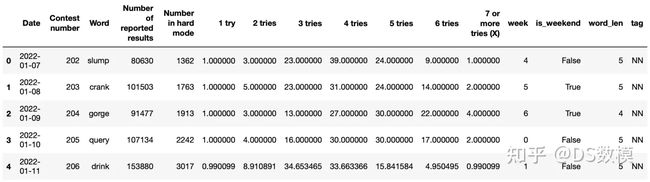
df = pd.read_excel('Problem_C_Data_Wordle.xlsx', header=1)
df=df[df.columns[1:]]
df.head()

预处理：

百分比之和可能不等于1，所以对其进行归一化

按照'Contest Number'对整个表进行升序排列

判断当前日期是否为周末，为周几

统计单词中字母个数，重复出现的字母算一次

对单词进行词性标注

df = pd.read_excel('Problem_C_Data_Wordle.xlsx', header=1)
df=df[df.columns[1:]]
#  对尝试次数进行归一化，使其结果和等于100
df = df.sort_values(by='Contest number', ignore_index=True)
percent = df[df.columns[5:]].sum(axis=1)
for column in df.columns[5:]:
    df[column]=df[column]/percent*100
# 判断当前日期为周几，周一为0，依次增加  
df['week']=df['Date'].apply(lambda x:x.weekday())
df['is_weekend'] = df['week'].apply(lambda x:x>4)
# 统计单词中字母的个数  
df['word_len'] = df['Word'].apply(lambda x:len(set(x)))
# 对单词进行词性标注
df['tag'] = df['Word'].apply(lambda x:nltk.pos_tag(nltk.word_tokenize(x))[0][1])
df.head()    

1 第一题

第一小问：

Q：报告结果的数量每天都在变化。开发一个模型来解释这种变化，并使用您的模型为2023年3月1日报告的结果数量创建一个预测区间。

首先判断是否与周几有关，如果有则将该参数加入模型中，如果没有则不加入

使用时间预测模型，或者二次函数训练，使用留一法等交叉验证方法得到关于模型准确率的描述。

第二小问：

Q：单词的任何属性是否会影响在硬模式下播放的报告分数百分比？如果是，怎么办？如果没有，为什么不呢？

A： 任何属性可以包括：唯一字母的数量，单词的词性，常见度，字母的词频

差异度分析，相关性分析

分析整体的星期几对得分均值的影响

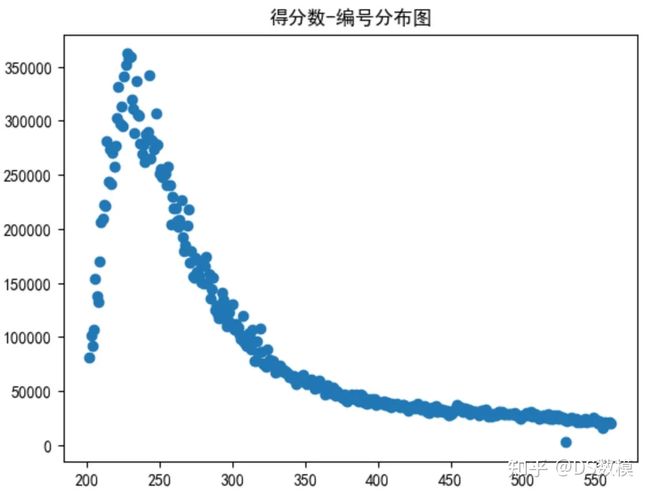
plt.scatter(df['Contest number'], df['Number of  reported results'])
plt.title('得分数-编号分布图')
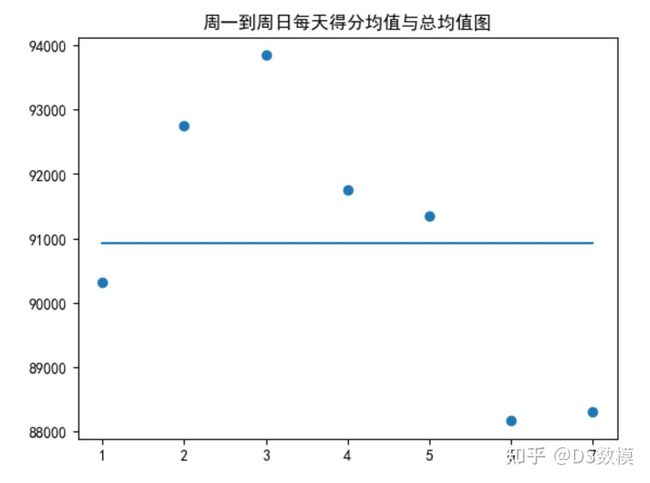
plt.show()

weeks = []
for week in range(7):
    df1 = df[df['week']==week]
    weeks.append(df1['Number of  reported results'].mean())
plt.scatter([i+1 for i in range(7)], weeks)
plt.plot([i+1 for i in range(7)], [df['Number of  reported results'].mean() for i in range(7)])
plt.title('周一到周日每天得分均值与总均值图')
# 其中直线为总均值图，散点图为每天的
plt.show()

# 整体得分与星期几之间的相关性
np.corrcoef(df['week'], df['Number of  reported results'])

可以看到，在整个时间段中，星期几与得分情况的相关性不大，甚至可以说不相关。

取得分总体趋于稳定后的区域，判断星期几对得分的影响

以上仅为第一问小部分思路（后续完善），剩余部分思路和其他全网具体配套代码、参考论文，以及其他题目思路，可以点击文末群名片获取