2023年数学建模美赛A题(A drought stricken plant communities)分析与编程
2023年数学建模美赛A题(A drought stricken plant communities)分析与编程
2023年数学建模美赛D题(Prioritizing the UN Sustainability Goals)分析与编程
特别提示:
1 本文介绍2023年美赛题目,进行深入分析;
2 本文首先对 A题进行深入分析,其它题目分析详见专题讨论;
3 最新更新:增加了多种群LK模型和例程。
文章目录
- 2023年数学建模美赛A题(A drought stricken plant communities)分析与编程
-
- 1. A题:A drought stricken plant communities(遭受旱灾的植物群落)
-
- 1.1 背景
- 1.2 要求
- 2. 问题分析
- 3. 种间竞争关系理论 Lotka-Volterra模型
-
- 3.1 Malthus人口理论
- 3.2 捕食者-猎物系统
- 3.3 Lotka-Volterra模型
- 3.4 Lotka-Volterra模型的数值模拟
- 3.4 三种群 Lotka-Volterra模型的数值模拟
- 4. Lotka-Volterra模型与全球植被模式
-
- 4.1 现存生物量一般动力学模型
- 4.2 包含n个物种的全球植被模式的一般动力学方程:
- 5. 参考数据
- 6. 参考资料
- 3. 微分方程模型求解
-
- 3.1 基本概念
- 3.2 微分方程的数学建模
- 3.3 微分方程的数值解法
- 4. SciPy 求解常微分方程(组)
-
- 4.1 一阶常微分方程(组)模型
- 4.2 scipy.integrate.odeint() 函数
- 5. 求洛伦兹(Lorenz)方程的数值解
-
- 6.1 例题 2:求洛伦兹(Lorenz)方程的数值解
- 6.2 洛伦兹(Lorenz)方程问题的编程步骤
- 6.3 洛伦兹(Lorenz)方程问题 Python 例程
- 6.4 洛伦兹(Lorenz)方程问题 Python 例程运行结果
2023年数学建模美赛A题(A drought stricken plant communities)分析与编程
1. A题:A drought stricken plant communities(遭受旱灾的植物群落)
1.1 背景
不同的植物群落对压力的反应不同。例如,草原对干旱非常敏感。干旱发生的频率和严重程度不同。但大量的观察表明,不同物种的数量对植物群落如何在连续多代干旱周期中的适应能力起到了重要作用。在一些仅有单一物种的植物群落中,后代不像有 4种或更多物种的群落中的个体植物那样容易适应干旱条件。这些观察引出了许多问题:例如,对于一个植物群落,要从这种局部生物多样性中受益,最少需要多少种物种?随着物种数量的增加,这种现象如何发展?这对植物群落的长期生存性意味着什么?
1.2 要求
考虑到植物群落中干旱适应性与物种数量的关系,您的任务是探索和更好地理解这一现象。具体地,您应该:
-
开发一个数学模型,预测植物群落随着不同的不规则天气周期的变化。在降水充足的时期应包括降雨的时间。该模型应考虑干旱周期中不同物种之间的相互作用。
-
探讨你能从你的模型中得出什么结论,关于植物群体与更大环境的长期相互作用。考虑以下问题:
- 要使植物群落受益,需要的不同植物物种数量是多少,随着物种数量的增加会发生什么?
- 社区中的物种类型如何影响你的结果?
- 未来天气周期中干旱发生的频率和变化范围的影响是什么?如果干旱较少,物种数量对总人口的影响是否相同?
- 污染和栖息地减少等其他因素如何影响你的结论?
- 您的模型表明应该采取什么措施以确保植物群落的长期生存力,对更大环境的影响是什么?
2. 问题分析
- 这是一道微分方程建模题目,建立模型是关键,模型求解并不难,基于模型的分析和讨论可以发挥想象力。
- 需要先找到相关研究论文,根据论文中提出物种与环境的关系的原理模型,建立微分方程的数学模型。论文中会给出具体的数学模型,可能是偏微分方程,能够求解就直接用;如果不会就简化为常微分方程也可以。
- 微分方程是描述系统的状态随时间和空间演化的数学工具。本题显然是研究几种物种的数量随时间的变化规律。
- **特别注意:**给定初始条件的一阶常微分方程(组)的标准形式是:
{ d y d t = f ( y , t ) y ( t 0 ) = y 0 \begin{cases} \begin{aligned} &\frac{dy}{dt} = f(y,t)\\ &y(t_0) = y_0 \end{aligned} \end{cases} ⎩ ⎨ ⎧dtdy=f(y,t)y(t0)=y0
微分方程是微分方程组,式中的 y 是数组向量,有几个物种就有几个变量, y i ( t ) y_i(t) yi(t) 表示物种 i 的总量随时间 t 的变化。
也就是说,可以先建立一种或两种物种的模型,分析变化趋势,再依次增多物种数量,分析变化趋势。- **特别注意:**构造外部条件及降雨量随时间的变化函数。
降雨量函数要满足题目要求:(1)不同的不规则天气周期,既要有干旱周期,又要有降水周期,还要有间隔周期;(2)干旱发生的频率和变化范围。
如何构造合理的降雨量函数,可以体现能力和创新的。思路一是设计的降雨量函数包含不同的可能模式,思路二是降雨量函数包括地球上典型的干旱模式,思路三是找到非洲地区的降雨量统计。- **特别注意:**污染和栖息地减少等其他因素的影响,需要在模型中增加一个系数,或者一项,反映污染和栖息地减少的影响。直接在模型中增加一个系数,比较简单。
进一步地,可以构思污染与种群总数相关,是一个随种群总数变化的系数。- **特别注意:**采取什么措施以确保植物群落的长期生存力,应该通过模型研究得到结论。
建议首先查找资料找到一种或多种靠谱的措施,然后将其量化为一个系数或一项加入模型(跟污染系数的原理是一致的),通过模型研究措施的影响,证明采取的措施是有效的。
简单地,既然污染会破坏环境,那么防止污染就可以保护环境,可以抑制污染系数的增大。
又如,水土保持能否量化为模型参数?食物链能否构造模型?- 微分方程模型求解,详见本文后续章节及博客:
- Python小白的数学建模课-09.微分方程模型(https://youcans.blog.csdn.net/article/details/117702996)
- Python小白的数学建模课-11.偏微分方程数值解法(https://youcans.blog.csdn.net/article/details/119755450)
本题要研究时间的变化,因此跟微分方程边值问题没什么关系。
3. 种间竞争关系理论 Lotka-Volterra模型
常微分方程与生态学有什么关联?生态学理论一直以种群动态为根基。它涌现出所谓生物多样性、空间分布格局、种间互作,也是功能性状、物候等话题在应用生态学中的归宿。
3.1 Malthus人口理论
1798年Malthus提出的人口理论被认为是生态学第一定律。Malthus指出,一切生物在“不受外力”的影响下,都以恒定的速率 k 增长。用微分方程可表达为:
d x d t = k x , k > 0 \frac{dx}{dt} = kx, k>0 dtdx=kx,k>0
该方程可直接用定积分(或不定积分)求解,结果为:
x = e k ( t − t 0 ) x 0 x=e^{k(t-t_0)}x_0 x=ek(t−t0)x0
这是一个指数曲线, 称为**「自然繁殖(normal reproduction)** 。
由于资源有限,当种群个体数过大时竞争激烈,故种群增长率会有所下降。所以 k 不是一个恒值,而是关于 x 的函数:
k = f ( x ) k=f(x) k=f(x)
函数f(x)应当是在x>0范围内随x增加而单调递减的函数。根据麦克劳林展开式:
f ( x ) = f ( 0 ) + d f ( x ) d x ∣ x = 0 ( x ) + o ( x ) ≈ a − b x f(x)=f(0)+\frac{df(x)}{dx}|_{x=0} (x)+o(x)\approx a-bx f(x)=f(0)+dxdf(x)∣x=0(x)+o(x)≈a−bx
当x足够小时,任何光滑函数可用线性函数作近似,因此:
d x d t = ( a − b x ) x \frac{dx}{dt}=(a-bx)x dtdx=(a−bx)x
求解微分方程,可得:
x = a e − a t + b x=\frac{a}{e^{-at}+b} x=e−at+ba
3.2 捕食者-猎物系统
Lotka(1910)和Volterra(1926)分别提出了捕食者–猎物系统的种群动态模型,称为Lotka–Volterra模型。该模型假设:捕食者、猎物相遇的几率与双方的种群个体数成正比;捕食者捕食猎物的频次与相遇频次成正比;捕食者种群增长率与捕食猎物的频次成正比;捕食者以恒定的速率死亡。
d x d t = k x − a x y d y d t = − l y + b x y \frac{dx}{dt}=kx-axy\\ \frac{dy}{dt}=-ly+bxy dtdx=kx−axydtdy=−ly+bxy
这个二元系统(捕食者+猎物)动态会如何变化:
► 捕食者、猎物种群动态的相位曲线如何?
► 捕食者、猎物种群动态是达到稳定平衡,还是有限环,还是混沌?或者说,相位曲线会呈螺旋形,造成系统崩溃或收敛到一个稳定点?
► 受到外界扰动时,捕食者、猎物种群动态还能保持稳定吗?
1 为什么到达平衡的时间经常是无穷大?
2 初值对Lotka–Volterra模型行为的影响
3 无扰动下Lotka–Volterra有限环大小不变
3.3 Lotka-Volterra模型
Lotka-Volterra模型(Lotka-Volterra种间竞争模型)是logistic模型(阻滞增长模型)的延伸。现设定如下参数:
- N1、N2:分别为两个物种的种群数量
- K1、K2:分别为两个物种的环境容纳量
- r1、r2 :分别为两个物种的种群增长率
依逻辑斯蒂模型有如下关系:
d N 1 d t = r 1 ∗ N 1 ∗ ( 1 − N 1 K 1 ) \frac{dN_1}{dt}=r_1 * N_1 * (1 - \frac{N_1}{K_1}) dtdN1=r1∗N1∗(1−K1N1)
其中:N/K 可以理解为已经利用的空间(称为“已利用空间项”),则 ( 1 − N / K ) (1-N/K) (1−N/K) 可以理解为尚未利用的空间(称为“未利用空间项”)。
当两个物种竞争或者利用同一空间时,“已利用空间项”还应该加上N2种群对空间的占用。则:
KaTeX parse error: Undefined control sequence: \alfa at position 53: …ac{N_1}{K_1} - \̲a̲l̲f̲a̲ ̲\frac{N_2}{K_2}…
其中,α:物种2对物种1的竞争系数,即每个N2个体所占用的空间相当于α个N1个体所占用空间。
则有,β:物种1对物种2的竞争系数,即每个N1个体所占用的空间相当于β个N2个体所占用空间。则另有:
d N 2 d t = r 2 ∗ N 2 ∗ ( 1 − N 2 K 2 − β N 1 K 1 ) \frac{dN_2}{dt}=r_2 * N_2 * (1 - \frac{N_2}{K_2} - \beta \frac{N_1}{K_1} ) dtdN2=r2∗N2∗(1−K2N2−βK1N1)
当物种N1种群(物种1)的环境容纳量为K1时,N1种群中每个个体对自身种群的增长抑制作用为1/K1;
同理,N2种群中每个个体对自身种群的增长抑制作用为1/K2。
另外,从(1)、(2)两个方程以及α、β的定义中可知:
- N2种群中每个个体对N1种群的影响为:α/K1
- N1种群中每个个体对N2种群的影响为:β/K2
因此,当物种2可以抑制物种1时,可以认为,物种2对物种1的影响 > 物种2对自身的影响,即 α/K1 > 1/K2。
整理后得:K2 > K1/α,同理有: - 物种2不能抑制物种1:K2 < K1/α
- 物种1可以抑制物种2:K1 > K2/β
- 物种1不能抑制物种2:K1 < K2/β
在竞争的过程中,由于K1、K2、α 以及 β 的数值不同,可能会产生如下四种结果:
(1)物种1能抑制物种2,物种2能抑制物种1:两物种都有可能得胜;
(2)物种1不能抑制物种2,物种2能抑制物种1:物种 2 得胜;
(3)物种1能抑制物种2,物种2不能抑制物种1:物种 2 得胜;
(4)物种1不能抑制物种2,物种2不能抑制物种1:两物种都不能抑制对方,形成稳定平衡。
结果4是一个稳定的平衡,无论N1和N2种群数量的组合(N1,N2)落在直角坐标系内哪一区域,最终都将使得N1种群和N2种群的数量趋向平衡点。
3.4 Lotka-Volterra模型的数值模拟
引入如下的相对种群规模变量
$$
u=\frac{U}{U^∗}=\frac{eγ}{β}U\
v=\frac{V}{V^∗}=\frac{γ}{a}V\
$$
以及无量纲时间 τ = α β t τ=αβt τ=αβt
原来的 Lotka-Volterra 方程组可以被改写成:
{ d u d τ = r ∗ ( u − u v ) d v d τ = 1 r ( u v − v ) \begin{cases} \frac{du}{dτ} = r*(u−uv)\\ \frac{dv}{dτ}=\frac{1}{r}(uv−v) \end{cases} {dτdu=r∗(u−uv)dτdv=r1(uv−v)
这里只剩下了一个自由的无量纲参数 r=αβ。如此便说明,在数值模拟时,我们只需要调节1个而不是4个参数,问题可以大大简化。r 值的大小和系统初始条件就可以完全确定解的行为。
from scipy.integrate import odeint # 导入 scipy.integrate 模块
import numpy as np # 导入 numpy包
import matplotlib.pyplot as plt # 导入 matplotlib包
def dyLV(y, t, r,mu): # SIR 模型,导数函数
u, v = y
du_dt = r * (u- u*v) # du/dt = r*(u-uv)
dv_dt = (u*v-v) / r # dv/dt = (uv-v)/r
return np.array([du_dt,dv_dt])
# 设置模型参数
r = [0.25, 0.5, 1.0, 2.0, 4.0]
mu = 1.0
colorlist = ['green','cyan','blue','orange','red']
tEnd = 20 # 预测日期长度
t = np.arange(0.0, tEnd, 1) # (start,stop,step)
u0 = 1.0 # 初值
v0 = 1.2 # 初值
Y0 = (u0, v0) # 微分方程组的初值
plt.figure(figsize=(10, 4))
for k in range(len(r)):
yt = odeint(dyLV, Y0, t, args=(r[k],mu)) # SIS 模型
plt.plot(t, yt[:, 0], color=colorlist[k], label=r"r = {}".format(r[k]))
plt.plot(t, yt[:, 1], '--', color=colorlist[k], label="r = {}".format(r[k]))
plt.xlabel('t')
plt.legend(loc='best') # youcans
plt.show()
下面几张图给出了不同 r 的取值对应的猎物和猎食者数量随时间的变化:
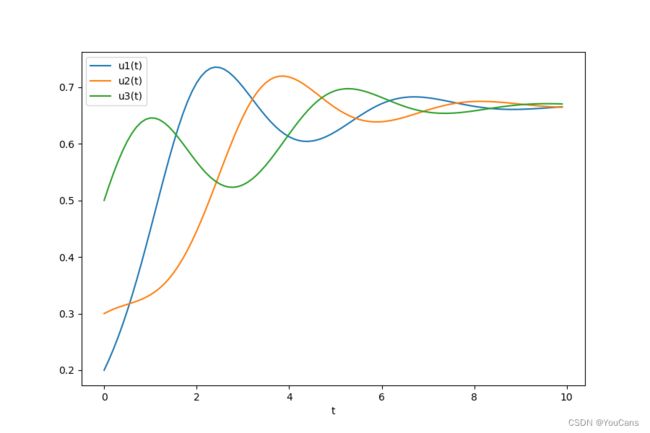
3.4 三种群 Lotka-Volterra模型的数值模拟
{ d u 1 d t = u 1 ∗ ( 1 − u 1 − α u 2 − β u 3 ) d u 2 d t = u 2 ∗ ( 1 − β u 1 − u 2 − α u 3 ) d u 3 d t = u 3 ∗ ( 1 − α u 1 − β u 2 − u 3 ) \begin{cases}\frac{du_1}{dt} = u_1 * (1 - u_1 -\alpha u_2 -\beta u_3)\\\frac{du_2}{dt} = u_2 * (1 - \beta u_1 - u_2 -\alpha u_3)\\\frac{du_3}{dt} = u_3 * (1 - \alpha u_1 - \beta u_2 - u_3)\end{cases}\\ ⎩ ⎨ ⎧dtdu1=u1∗(1−u1−αu2−βu3)dtdu2=u2∗(1−βu1−u2−αu3)dtdu3=u3∗(1−αu1−βu2−u3)
from scipy.integrate import odeint # 导入 scipy.integrate 模块
import numpy as np # 导入 numpy包
import matplotlib.pyplot as plt # 导入 matplotlib包
def dyLV3(y, t, alfa, beta): # 3物种LK模型,导数函数
u1, u2, u3 = y
du1_dt = u1 * (1 - u1 - alfa*u2 - beta*u3)
du2_dt = u2 * (1- beta*u1 -u2 - alfa*u3)
du3_dt = u3 * (1- alfa*u1 -beta*u2 - u3)
return np.array([du1_dt, du2_dt, du3_dt])
# 设置模型参数
alfa, beta = 1.5, -1.0
tEnd = 10 # 预测长度
t = np.arange(0.0, tEnd, 0.1) # (start,stop,step)
u10, u20, u30 = 0.2, 0.3, 0.5 # 初值
Y0 = (u10, u20, u30) # 微分方程组的初值
plt.figure(figsize=(9,6))
# plt.subplot(121), plt.title("1. u(r)")
yt = odeint(dyLV3, Y0, t, args=(alfa, beta)) # SIS 模型
plt.plot(t, yt[:,0], label="u1(t)")
plt.plot(t, yt[:,1], label="u2(t)")
plt.plot(t, yt[:,2], label="u3(t)")
plt.xlabel('t')
plt.legend(loc='best')
plt.show()
4. Lotka-Volterra模型与全球植被模式
Svirezhev Y:Lotka-Volterra模型与全球植被模式。Ecological Modelling,2000,135
4.1 现存生物量一般动力学模型
《资源环境数学模型手册》 (2019). 标准Lotka-Volterra模型
d B d t = P − m R ∗ B \frac{dB}{dt} = P - m_R*B dtdB=P−mR∗B
式中,B 为现存生物量;P 是净生产率; r R = 1 / m R r_R=1/m_R rR=1/mR 是碳在生物量中实际停留时间;一般来说, P = P ( T , W , I , C ) P=P(T,W,I,C) P=P(T,W,I,C),其中T是时间,W是土壤含水量,I是光照,C是大气中碳浓度。
m R = m + G ( B , B s ) m_R = m + G(B,B_s) mR=m+G(B,Bs)
式中, B s B_s Bs 为其他竞争物种的生物量;可理解为某一物种的平均生理寿命。
4.2 包含n个物种的全球植被模式的一般动力学方程:
d B i d t = P i ( B i , T , H ) − m i R ∗ B i \frac{dB_i}{dt} = P_i(B_i,T,H) - m_i^R*B_i dtdBi=Pi(Bi,T,H)−miR∗Bi
式中,T 和H是这一空间位置的年平均温度和年降水量;P_i 净初级生产力;miR为第i类物种的平均生理寿命。
假设竞争系数是空间无关的,即,便可得到标准的Lotka-Volterra模型:
∂ B i ∂ t = B i ∗ [ g i ( T , H ) − m i − ∑ γ i j B j \frac{\partial B_i}{\partial t} = B_i * [g_i(T,H) - m_i - \sum {\gamma _{ij} B_j} ∂t∂Bi=Bi∗[gi(T,H)−mi−∑γijBj
5. 参考数据
6. 参考资料
(1) 植被变化与降水量、降水变率的关系
(2) 长期降水量变化下荒漠草原植物生物量、多样性及其影响因素研究
(3) 荒漠植物幼苗对模拟降水量变化的响应
(4) 中亚地区1982年至2002年植被指数与气温和降水的相关性分析
(5) 内蒙古典型草原生长季内植物生长动态的数学模型与计算机模拟研究
(6) 降水量的季节分配对羊草草原群落地上部生物量影响的数学模型
(7) 干旱区荒漠植被生态需水量计算方法研究
(8) 干旱半干旱区植被生态需水量计算方法评述
(9) 基于数学模型的干旱区植被耗水量估算
(10) 乌审旗植被覆盖度动态变化及其与降水量的关系
(11) 归一化植被指数与降水量,土壤湿度的关系
以下内容只供参考
3. 微分方程模型求解
3.1 基本概念
微分方程是描述系统的状态随时间和空间演化的数学工具。物理中许多涉及变力的运动学、动力学问题,如空气的阻力为速度函数的落体运动等问题,很多可以用微分方程求解。微分方程在化学、工程学、经济学和人口统计等领域也有广泛应用。
具体来说,微分方程是指含有未知函数及其导数的关系式。
- 微分方程按自变量个数分为:只有一个自变量的常微分方程(Ordinary Differential Equations)和包含两个或两个以上独立变量的偏微分方程(Partial Differential Equations)。
- 微分方程按阶数分为:一阶、二阶、高阶,微分方程的阶数取决于方程中最高次导数的阶数。
- 微分方程还可以分为:(非)齐次,常(变)系数,(非)线性,初值问题/边界问题…
3.2 微分方程的数学建模
微分方程的数学建模其实并不复杂,基本过程就是分析题目属于哪一类问题、可以选择什么微分方程模型,然后如何使用现有的微分方程模型建模。
在数学、力学、物理、化学等各个学科领域的课程中,针对该学科的各种问题都会建立适当的数学模型。在中学课程中,各学科的数学模型主要是线性或非线性方程,而在大学物理和各专业的课程中,越来越多地出现用微分方程描述的数学模型。
数学建模中的微分方程问题,通常还是这些专业课程中相对简单的模型,专业课程的教材在介绍一个模型时,往往都做了非常详细的讲解。只要搞清楚问题的类型、选择好数学模型,建模和求解并不是很难,而且在撰写论文时对问题背景、使用范围、假设条件、求解过程有大量现成的内容可以复制参考。
希望你在学习本系列之后,会发现微分方程模型是数学建模中最容易的题型:模型找教材,建模找例题,求解有例程,讨论有套路,论文够档次。
3.3 微分方程的数值解法
在学习专业课程时,经常会推导和求解微分方程的解析解,小白对微分方程模型的恐惧就是从高等数学“微分方程”开始,经过专业课的不断强化而形成的。实际上,只有很少的微分方程可以解析求解,大多数的微分方程只能采用数值方法进行求解。
微分方程的数值求解是先把时间和空间离散化,然后将微分化为差分,建立递推关系,然后反复进行迭代计算,得到任意时间和空间的值。
如果你还是觉得头晕目眩,我们可以说的更简单一些。建模就是把专业课教材上的公式抄下来,求解就是把公式的参数输入到 Python 函数中。
我们先说求解。求解常微分方程的基本方法,有欧拉法、龙格库塔法等,可以详见各种教材,撰写数模竞赛论文时还是可以抄几段的。本文沿用“编程方案”的概念,不涉及这些算法的具体内容,只探讨如何使用 Python 的工具包、库函数,零基础求解微分方程模型。
我们的选择是 Python 常用工具包三剑客:Scipy、Numpy 和 Matplotlib:
- Scipy 是 Python 算法库和数学工具包,包括最优化、线性代数、积分、插值、特殊函数、傅里叶变换、信号和图像处理、常微分方程求解等模块。有人介绍 Scipy 就是 Python 语言的 Matlab,所以大部分数学建模问题都可以用它搞定。
- Numpy 提供了高维数组的实现与计算的功能,如线性代数运算、傅里叶变换及随机数生成,另外还提供了与 C/C++ 等语言的集成工具。
- Matplotlib 是可视化工具包,可以方便地绘制各种数据可视化图表,如折线图、散点图、直方图、条形图、箱形图、饼图、三维图,等等。
顺便说一句,还有一个 Python 符号运算工具包 SymPy,以解析方式求解积分、微分方程,也就是说给出的结果是微分方程的解析解表达式。很牛,但只能求解有解析解的微分方程,所以,你知道就可以了。
4. SciPy 求解常微分方程(组)
4.1 一阶常微分方程(组)模型
给定初始条件的一阶常微分方程(组)的标准形式是:
{ d y d t = f ( y , t ) y ( t 0 ) = y 0 \begin{cases} \begin{aligned} &\frac{dy}{dt} = f(y,t)\\ &y(t_0) = y_0 \end{aligned} \end{cases} ⎩ ⎨ ⎧dtdy=f(y,t)y(t0)=y0
式中的 y 在常微分方程中是标量,在常微分方程组中是数组向量。
4.2 scipy.integrate.odeint() 函数
SciPy 提供了两种方式求解常微分方程:基于 odeint 函数的 API 比较简单易学,基于 ode 类的面向对象的 API 更加灵活。
**scipy.integrate.odeint() **是求解微分方程的具体方法,通过数值积分来求解常微分方程组。在 odeint 函数内部使用 FORTRAN 库 odepack 中的 lsoda,可以求解一阶刚性系统和非刚性系统的初值问题。官网介绍详见: scipy.integrate.odeint — SciPy v1.6.3 Reference Guide 。
scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)
odeint 的主要参数:
求解标准形式的微分方程(组)主要使用前三个参数:
- func: callable(y, t, …) 导数函数 f ( y , t ) f(y,t) f(y,t) ,即 y 在 t 处的导数,以函数的形式表示
- y0: array: 初始条件 y 0 y_0 y0,对于常微分方程组 y 0 y_0 y0 则为数组向量
- t: array: 求解函数值对应的时间点的序列。序列的第一个元素是与初始条件 y 0 y_0 y0 对应的初始时间 t 0 t_0 t0;时间序列必须是单调递增或单调递减的,允许重复值。
其它参数简介如下:
-
args: 向导数函数 func 传递参数。当导数函数 f ( y , t , p 1 , p 2 , . . ) f(y,t,p1,p2,..) f(y,t,p1,p2,..) 包括可变参数 p1,p2… 时,通过 args =(p1,p2,…) 可以将参数p1,p2… 传递给导数函数 func。argus 的用法参见 2.4 中的实例2。
-
Dfun: func 的雅可比矩阵,行优先。如果 Dfun 未给出,则算法自动推导。
-
col_deriv: 自动推导 Dfun的方式。
-
printmessg: 布尔值。控制是否打印收敛信息。
-
其它参数用于控制求解算法的参数,一般情况可以忽略。
odeint 的主要返回值:
- y: array 数组,形状为 (len(t),len(y0),给出时间序列 t 中每个时刻的 y 值。
5. 求洛伦兹(Lorenz)方程的数值解
6.1 例题 2:求洛伦兹(Lorenz)方程的数值解
洛伦兹(Lorenz)混沌吸引子的轨迹可以由如下的 3个微分方程描述:
{ d x d t = σ ( y − x ) d y d t = x ( ρ − z ) − y d z d t = x y − β z \begin{cases} \begin{aligned} &\frac{dx}{dt} = \sigma (y-x)\\ &\frac{dy}{dt} = x (\rho-z) - y\\ &\frac{dz}{dt} = xy - \beta z\\ \end{aligned} \end{cases} ⎩ ⎨ ⎧dtdx=σ(y−x)dtdy=x(ρ−z)−ydtdz=xy−βz
洛伦兹方程将大气流体运动的强度 x 与水平和垂直方向的温度变化 y 和 z 联系起来,进行大气对流系统的模拟,现已广泛应用于天气预报、空气污染和全球气候变化的研究。参数 σ \sigma σ 称为普兰特数, ρ \rho ρ 是规范化的瑞利数, β \beta β 和几何形状相关。洛伦兹方程是非线性微分方程组,无法求出解析解,只能使用数值方法求解。
6.2 洛伦兹(Lorenz)方程问题的编程步骤
以该题为例讲解 scipy.integrate.odeint() 求解常微分方程初值问题的步骤:
-
导入 scipy、numpy、matplotlib 包;
-
定义导数函数 lorenz(W, t, p, r, b)
注意 odeint() 函数中定义导数函数的标准形式是 f ( y , t ) f(y,t) f(y,t) ,对于微分方程组 y 表示向量。
为避免混淆,我们记为 W = [ x , y , z ] W=[x,y,z] W=[x,y,z],函数 lorenz(W,t) 定义导数函数 f ( W , t ) f(W,t) f(W,t) 。
用 p,r,b 分别表示方程中的参数 σ 、 ρ 、 β \sigma、\rho、\beta σ、ρ、β,则对导数定义函数编程如下:
# 导数函数,求 W=[x,y,z] 点的导数 dW/dt
def lorenz(W,t,p,r,b):
x, y, z = W # W=[x,y,z]
dx_dt = p*(y-x) # dx/dt = p*(y-x), p: sigma
dy_dt = x*(r-z) - y # dy/dt = x*(r-z)-y, r:rho
dz_dt = x*y - b*z # dz/dt = x*y - b*z, b;beta
return np.array([dx_dt,dy_dt,dz_dt])
-
定义初值 W 0 W_0 W0 和 W W W 的定义区间 [ t 0 , t ] [t_0,\ t] [t0, t];
-
调用 odeint() 求 W W W 在定义区间 [ t 0 , t ] [t_0,\ t] [t0, t] 的数值解。
注意例程中通过 args=paras 或 args = (10.0,28.0,3.0) 将参数 (p,r,b) 传递给导数函数 lorenz(W,t,p,r,b)。参数 (p,r,b) 当然也可以不作为函数参数传递,而是在导数函数 lorenz() 中直接设置。但例程的参数传递方法,使导数函数结构清晰、更为通用。另外,对于可变参数问题,使用这种参数传递方式就非常方便。
6.3 洛伦兹(Lorenz)方程问题 Python 例程
# 2. 求解微分方程组初值问题(scipy.integrate.odeint)
from scipy.integrate import odeint # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 导数函数, 求 W=[x,y,z] 点的导数 dW/dt
def lorenz(W,t,p,r,b): # by youcans
x, y, z = W # W=[x,y,z]
dx_dt = p*(y-x) # dx/dt = p*(y-x), p: sigma
dy_dt = x*(r-z) - y # dy/dt = x*(r-z)-y, r:rho
dz_dt = x*y - b*z # dz/dt = x*y - b*z, b;beta
return np.array([dx_dt,dy_dt,dz_dt])
t = np.arange(0, 30, 0.01) # 创建时间点 (start,stop,step)
paras = (10.0, 28.0, 3.0) # 设置 Lorenz 方程中的参数 (p,r,b)
# 调用ode对lorenz进行求解, 用两个不同的初始值 W1、W2 分别求解
W1 = (0.0, 1.00, 0.0) # 定义初值为 W1
track1 = odeint(lorenz, W1, t, args=(10.0, 28.0, 3.0)) # args 设置导数函数的参数
W2 = (0.0, 1.01, 0.0) # 定义初值为 W2
track2 = odeint(lorenz, W2, t, args=paras) # 通过 paras 传递导数函数的参数
# 绘图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2], color='magenta') # 绘制轨迹 1
ax.plot(track2[:,0], track2[:,1], track2[:,2], color='deepskyblue') # 绘制轨迹 2
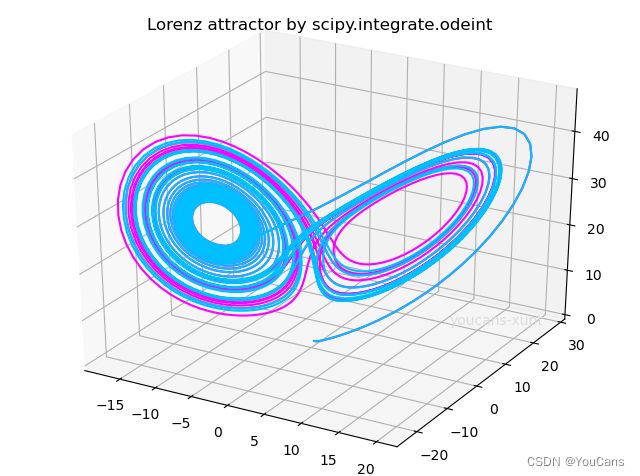
ax.set_title("Lorenz attractor by scipy.integrate.odeint")
plt.show()
6.4 洛伦兹(Lorenz)方程问题 Python 例程运行结果
【本节完】