目录
- Stack的特点:先进后出(FILO)
- 使用场景:十进制转2进制 函数调用堆栈
js里没有栈,但是可以用数组模拟
42/2 42%2=0 21/2 21%2=1 10/2 10%2=0 5/2 5%2=1 2/2 2%2=0 1/2 1%2=1 stack: [0,1,0,1,0,1] res: 1 0 1 0 1 0 fn1(){ fn2() } fn2(){ fn3() } fn3(){} fn1() stack:[fn1,fn2,fn3]- 栈的时间复杂度:入栈和出栈
O(1),查找O(n)
155. 最小栈 (easy)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。示例 1:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]输出:
[null,null,null,null,-3,null,0,-2]解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.提示:
-231 <= val <= 231 - 1
pop、top 和 getMin 操作总是在 非空栈 上调用
push, pop, top, and getMin最多被调用 3 * 104 次
- 思路:定义两个栈stack和min_stack,stack正常push,min_stack只会push需要入栈和栈顶中较小的元素。getMin返回min_stack栈顶元素,top返回stack栈顶元素。
- 复杂度:所有操作的时间复杂度是
O(1)
js:
var MinStack = function () {
this.stack = [];
this.min_stack = [Infinity];
};
//stack正常push,min_stack只会push需要入栈和栈顶中较小的元素
MinStack.prototype.push = function (x) {
this.stack.push(x);
this.min_stack.push(Math.min(this.min_stack[this.min_stack.length - 1], x));
};
//stack正常pop,min_stack正常pop
MinStack.prototype.pop = function () {
this.stack.pop();
this.min_stack.pop();
};
//返回stack栈顶元素
MinStack.prototype.top = function () {
return this.stack[this.stack.length - 1];
};
//返回min_stack栈顶元素
MinStack.prototype.getMin = function () {
return this.min_stack[this.min_stack.length - 1];
};946. 验证栈序列 (medium)
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。提示:
1 <= pushed.length <= 1000
0 <= pushed[i] <= 1000
pushed 的所有元素 互不相同
popped.length == pushed.length
popped 是 pushed 的一个排列
- 思路:用栈模拟出栈入栈的过程,当popped中index指向的位置的元素和stack栈顶的元素一致时,出栈 并且
index++,最后判断stack是否为空 - 复杂度:时间复杂度
O(n),pushed中的元素入栈出栈一次,空间复杂度O(n),栈的大小
js:
const validateStackSequences = (pushed, popped) => {
const stack = [];//用栈模拟出栈入栈的过程
let index = 0;
const len = pushed.length;
for (let i = 0; i < len; i++) {
stack.push(pushed[i]);
//当popped中index指向的位置的元素和stack栈顶的元素一致时,出栈 并且 index++
while (popped[index] !== undefined && popped[index] === stack[stack.length - 1]) {
stack.pop();
index++;
}
}
return !stack.length;//最后判断stack是否为空
};232. 用栈实现队列 (easy)
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。示例 1:
输入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false提示:
1 <= x <= 9
最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)进阶:
你能否实现每个操作均摊时间复杂度为 O(1) 的队列?换句话说,执行 n 个操作的总时间复杂度为 O(n) ,即使其中一个操作可能花费较长时间。
方法1.栈
- 思路:这是一道模拟题,不涉及到具体算法,考察的就是对栈和队列的掌握程度。使用栈来模式队列的行为,如果仅仅用一个栈,是一定不行的,所以需要两个栈一个输入栈,一个输出栈,这里要注意输入栈和输出栈的关系。在push数据的时候,只要数据放进输入栈就好,但在pop的时候,操作就复杂一些,输出栈如果为空,就把进栈数据全部导入进来(注意是全部导入),再从出栈弹出数据,如果输出栈不为空,则直接从出栈弹出数据就可以了。最后如果进栈和出栈都为空的话,说明模拟的队列为空了。
- 复杂度分析:push时间复杂度
O(1),pop时间复杂度为O(n),因为pop的时候,输出栈为空,则把输入栈所有的元素加入输出栈。空间复杂度O(n),两个栈空间
js:
var MyQueue = function() {
//准备两个栈
this.stack1 = [];
this.stack2 = [];
};
MyQueue.prototype.push = function(x) {//push的时候加入输入栈
this.stack1.push(x);
};
MyQueue.prototype.pop = function() {
const size = this.stack2.length;
if(size) {//push的时候判断输出栈是否为空
return this.stack2.pop();//不为空则输出栈出栈
}
while(this.stack1.length) {//输出栈为空,则把输入栈所有的元素加入输出栈
this.stack2.push(this.stack1.pop());
}
return this.stack2.pop();
};
MyQueue.prototype.peek = function() {
const x = this.pop();//查看队头的元素 复用pop方法,然后在让元素push进输出栈
this.stack2.push(x);
return x;
};
MyQueue.prototype.empty = function() {
return !this.stack1.length && !this.stack2.length
};20. 有效的括号 (easy)
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。示例 1:
输入:s = "()"
输出:true
示例 2:输入:s = "()[]{}"
输出:true
示例 3:输入:s = "(]"
输出:false提示:
1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成
方法1.栈
- 思路:首先如果字符串能组成有效的括号,则长度一定是偶数,我们可以遍历字符串,遇到左括号则暂存,期待后面有右括号可以和它匹配,如果遇到右括号则检查是否能和最晚暂存的做括号匹配。这就和栈这种数据结构先进后出的特性相吻合了。所以我们可以准备一个栈存放括号对,遍历字符串的时候,如果遇到左括号入栈,遇到右括号则判断右括号是否能和栈顶元素匹配,在循环结束的时候还要判断栈是否为空,如果不为空,则不是有效括号匹配的字符串
- 复杂度分析:时间复杂度
O(n),空间复杂度O(n),n为字符串的长度
js:
var isValid = function(s) {
const n = s.length;
if (n % 2 === 1) {//如果字符串能组成有效的括号,则长度一定是偶数
return false;
}
const pairs = new Map([//用栈存储括号对
[')', '('],
[']', '['],
['}', '{']
]);
const stk = [];
for (let ch of s){//循环字符串
if (pairs.has(ch)) {
//遇到右括号则判断右括号是否能和栈顶元素匹配
if (!stk.length || stk[stk.length - 1] !== pairs.get(ch)) {
return false;
}
stk.pop();
} else {
stk.push(ch);//如果遇到左括号入栈
}
};
return !stk.length;//循环结束的时候还要判断栈是否为空
};445. 两数相加 II (medium)
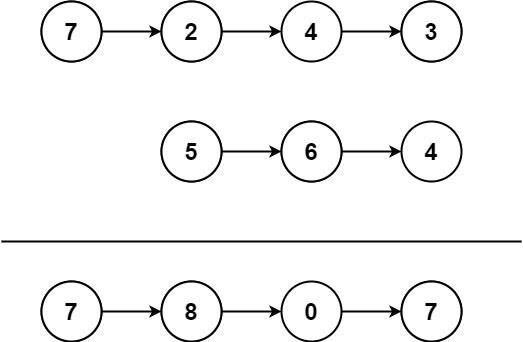
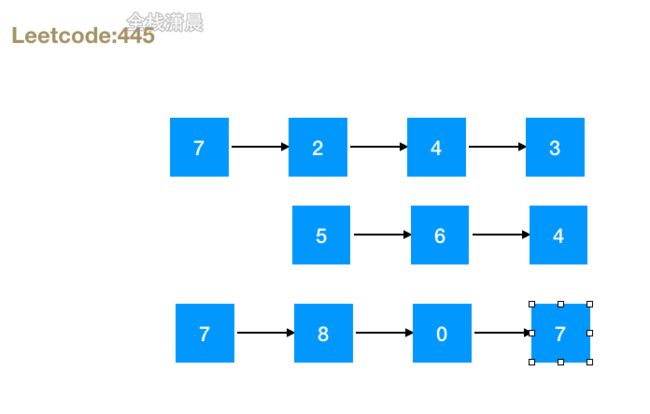
给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
你可以假设除了数字 0 之外,这两个数字都不会以零开头。
示例1:
输入:l1 = [7,2,4,3], l2 = [5,6,4]
输出:[7,8,0,7]
示例2:输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[8,0,7]
示例3:输入:l1 = [0], l2 = [0]
输出:[0]提示:
链表的长度范围为 [1, 100]
0 <= node.val <= 9
输入数据保证链表代表的数字无前导 0进阶:如果输入链表不能翻转该如何解决?
- 思路:将两个链表的节点都推入栈中,然后不断出栈,计算每个位置的值和进位,串连成一个新的链表
- 复杂度:时间复杂度
O(max(m,n)),m,n是两个链表的长度,空间复杂度O(m+n)
js:
var addTwoNumbers = function(l1, l2) {
const stack1 = [];
const stack2 = [];
while (l1 || l2) {//两链表入栈
if (l1) {
stack1.push(l1.val);
l1 = l1.next;
}
if (l2) {
stack2.push(l2.val);
l2 = l2.next;
}
}
let carry = 0;
let ansList = null;
while (stack1.length || stack2.length || carry !== 0) {//不断出栈
const s1 = stack1.length ? stack1.pop() : 0;
const s2 = stack2.length ? stack2.pop() : 0;
let val = s1 + s2 + carry;
carry = parseInt(val / 10);//计算进位
val = val % 10;//计算当前节点的值
const curNode = new ListNode(val);
curNode.next = ansList;//向链表前插入新节点
ansList = curNode;//重新赋值ansList
}
return ansList;
};682. 棒球比赛 (easy)
你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。
比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 ops,其中 ops[i] 是你需要记录的第 i 项操作,ops 遵循下述规则:
整数 x - 表示本回合新获得分数 x
"+" - 表示本回合新获得的得分是前两次得分的总和。题目数据保证记录此操作时前面总是存在两个有效的分数。
"D" - 表示本回合新获得的得分是前一次得分的两倍。题目数据保证记录此操作时前面总是存在一个有效的分数。
"C" - 表示前一次得分无效,将其从记录中移除。题目数据保证记录此操作时前面总是存在一个有效的分数。
请你返回记录中所有得分的总和。示例 1:
输入:ops = ["5","2","C","D","+"]
输出:30
解释:
"5" - 记录加 5 ,记录现在是 [5]
"2" - 记录加 2 ,记录现在是 [5, 2]
"C" - 使前一次得分的记录无效并将其移除,记录现在是 [5].
"D" - 记录加 2 * 5 = 10 ,记录现在是 [5, 10].
"+" - 记录加 5 + 10 = 15 ,记录现在是 [5, 10, 15].
所有得分的总和 5 + 10 + 15 = 30
示例 2:输入:ops = ["5","-2","4","C","D","9","+","+"]
输出:27
解释:
"5" - 记录加 5 ,记录现在是 [5]
"-2" - 记录加 -2 ,记录现在是 [5, -2]
"4" - 记录加 4 ,记录现在是 [5, -2, 4]
"C" - 使前一次得分的记录无效并将其移除,记录现在是 [5, -2]
"D" - 记录加 2 * -2 = -4 ,记录现在是 [5, -2, -4]
"9" - 记录加 9 ,记录现在是 [5, -2, -4, 9]
"+" - 记录加 -4 + 9 = 5 ,记录现在是 [5, -2, -4, 9, 5]
"+" - 记录加 9 + 5 = 14 ,记录现在是 [5, -2, -4, 9, 5, 14]
所有得分的总和 5 + -2 + -4 + 9 + 5 + 14 = 27
示例 3:输入:ops = ["1"]
输出:1提示:
1 <= ops.length <= 1000
ops[i] 为 "C"、"D"、"+",或者一个表示整数的字符串。整数范围是 [-3 104, 3 104]
对于 "+" 操作,题目数据保证记录此操作时前面总是存在两个有效的分数
对于 "C" 和 "D" 操作,题目数据保证记录此操作时前面总是存在一个有效的分数
- 复杂度:时间复杂度
O(n),空间复杂度O(n)
js:
let calPoints = function(ops) {
let res = [];
for(let i = 0; i < ops.length; i++){
switch(ops[i]){
case "C":
res.pop();
break;
case "D":
res.push(+res[res.length - 1] * 2);
break;
case "+":
res.push(+res[res.length - 1] + +res[res.length - 2]);
break;
default:
res.push(+ops[i]);
}
}
return res.reduce((i, j) => i + j, 0);
};视频讲解:传送门